Interested Article - Ортогональная система координат

- 2021-02-22
- 1
Ортогональными называются криволинейные координаты , в которых метрический тензор имеет диагональный вид.
- ,
где - размерность пространства. Скалярный фактор
равен корню квадратному от диагональных компонент метрического тензора, или длине локального базисного вектора .
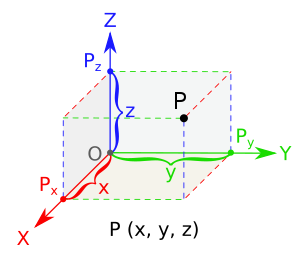
В ортогональных системах координат координатные поверхности ортогональны друг другу. В частности, в декартовой системе координат ортогональны друг другу координатные оси , и .
Выбор той или иной системы ортогональных координат определяется симметрией системы. Например, при решении задачи о распространении электромагнитной волны от точечного источника выгодно пользоваться сферической системой координат ; при решении задачи о колебании мембраны предпочтительней цилиндрическая система координат .
Математические преобразования
Базисные векторы
В ортогональных системах скалярное произведение базисных векторов равно:
В большинстве случаев используют нормированные базисные векторы, для которых .
Для нормированных базисных векторов , где — символ Кронекера .
Скалярное произведение
Скалярное произведение векторов в ортогональных системах вычисляется по формуле:
- .
- 2021-02-22
- 1