Interested Article - B-дерево

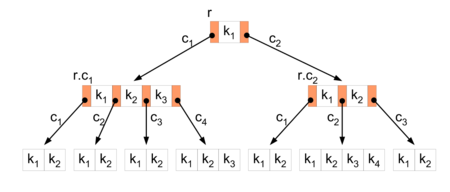
B-дерево — структура данных , дерево поиска. С точки зрения внешнего логического представления — сбалансированное , сильно ветвистое дерево . Часто используется для хранения данных во внешней памяти ^{[

источник не указан 251 день

]} .

Использование B-деревьев впервые было предложено Р. Бэйером ( англ. R. Bayer) и Э. МакКрейтом ( англ. E. McCreight) в 1970 году .

Сбалансированность означает, что длины любых двух путей от корня до листьев различаются не более, чем на единицу.

Ветвистость дерева — это свойство каждого узла дерева ссылаться на большое число узлов-потомков.

С точки зрения физической организации B-дерево представляется как мультисписочная структура страниц памяти, то есть каждому узлу дерева соответствует блок памяти (страница). Внутренние и листовые страницы обычно имеют разную структуру.

Применение

Структура B-дерева применяется для организации индексов во многих современных СУБД .

B-дерево может применяться для структурирования (индексирования) информации на жёстком диске (как правило, метаданных). Время доступа к произвольному блоку на жёстком диске очень велико (порядка миллисекунд), поскольку оно определяется скоростью вращения диска и перемещения головок. Поэтому важно уменьшить количество узлов, просматриваемых при каждой операции. Использование поиска по списку каждый раз для нахождения случайного блока могло бы привести к чрезмерному количеству обращений к диску вследствие необходимости последовательного прохода по всем его элементам, предшествующим заданному, тогда как поиск в B-дереве, благодаря свойствам сбалансированности и высокой ветвистости, позволяет значительно сократить количество таких операций.

Относительно простая реализация алгоритмов и существование готовых библиотек (в том числе для C ) для работы со структурой B-дерева обеспечивают популярность применения такой организации памяти в самых разнообразных программах, работающих с большими объёмами данных.

Структура и принципы построения

B-деревом называется дерево, удовлетворяющее следующим свойствам:

Ключи в каждом узле обычно упорядочены для быстрого доступа к ним. Корень содержит от 1 до 2t-1 ключей. Любой другой узел содержит от t-1 до 2t-1 ключей. Листья не являются исключением из этого правила. Здесь t — параметр дерева, не меньший 2 (и обычно принимающий значения от 50 до 2000 ).
У листьев потомков нет. Любой другой узел, содержащий ключи K 1 {\displaystyle K_{1}} , …, K n {\displaystyle K_{n}} , содержит n + 1 {\displaystyle n+1} потомков. При этом
1. Первый потомок и все его потомки содержат ключи из интервала $(-\infty ,K_{1})$ $(-\infty, K_1)$
2. Для $2\leq i\leq n$ $2\le i\le n$ , i-й потомок и все его потомки содержат ключи из интервала $(K_{i-1},K_{i})$ $(K_{i-1}, K_i)$
3. $(n+1)$ $(n+1)$ -й потомок и все его потомки содержат ключи из интервала $(K_{n},\infty)$ $(K_n, \infty)$
Глубина всех листьев одинакова.

Свойство 2 можно сформулировать иначе: каждый узел B-дерева, кроме листьев, можно рассматривать как упорядоченный список, в котором чередуются ключи и указатели на потомков.

Поиск

Если ключ содержится в корне, он найден. Иначе определяем интервал и идём к соответствующему потомку. Повторяем.

Добавление ключа

Будем называть деревом потомков некоего узла поддерево, состоящее из этого узла и его потомков.

Вначале определим функцию, которая добавляет ключ K к дереву потомков узла x. После выполнения функции во всех пройденных узлах, кроме, может быть, самого узла x, будет меньше $2t-1$ $2t-1$ , но не меньше $t-1$ $t-1$ , ключей.

Если х — не лист,
1. Определяем интервал, где должен находиться K. Пусть y — соответствующий потомок.
2. Рекурсивно добавляем K к дереву потомков y.
3. Если узел y полон, то есть содержит $2t-1$ $2t-1$ ключей, расщепляем его на два. Узел $y_{1}$ $y_1$ получает первые $t-1$ $t-1$ из ключей y и первые $t$ $t$ его потомков, а узел $y_{2}$ $y_2$ — последние $t-1$ $t-1$ из ключей y и последние $t$ $t$ его потомков. Медианный из ключей узла y попадает в узел х, а указатель на y в узле x заменяется указателями на узлы $y_{1}$ $y_1$ и $y_{2}$ $y_2$ .
Если x — лист, просто добавляем туда ключ K.

Теперь определим добавление ключа K ко всему дереву. Буквой R обозначается корневой узел.

Добавим K к дереву потомков R.
Если R содержит теперь $2t-1$ $2t-1$ ключей, расщепляем его на два. Узел $R_{1}$ $R_{1}$ получает первые $t-1$ $t-1$ из ключей R и первые $t$ $t$ его потомков, а узел $R_{2}$ $R_{2}$ — последние $t-1$ $t-1$ из ключей R и последние $t$ $t$ его потомков. Медианный из ключей узла R попадает во вновь созданный узел, который становится корневым. Узлы $R_{1}$ $R_{1}$ и $R_{2}$ $R_{2}$ становятся его потомками.

Удаление ключа

Если корень одновременно является листом, то есть в дереве всего один узел, мы просто удаляем ключ из этого узла. В противном случае сначала находим узел, содержащий ключ, запоминая путь к нему. Пусть этот узел — $x$ $x$ .

Если $x$ $x$ — лист, удаляем оттуда ключ. Если в узле $x$ $x$ осталось не меньше $t-1$ $t-1$ ключей, мы на этом останавливаемся. Иначе мы смотрим на количество ключей в двух соседних узлах-братьях. Если соседний правый узел есть, и в нём не менее $t$ $t$ ключей, мы добавляем в $x$ $x$ ключ-разделитель между ним и соседним правым узлом, а на место этого ключа ставим первый ключ соседнего правого узла, после чего останавливаемся. Если это не так, но есть соседний левый узел, и в нём не менее $t$ $t$ ключей, мы добавляем в $x$ $x$ ключ-разделитель между ним и соседним левым узлом, а на место этого ключа ставим последний ключ соседнего левого узла, после чего останавливаемся. Наконец, если и с левым ключом не получилось, мы объединяем узел $x$ $x$ с соседним левым или правым узлом, и в объединённый узел перемещаем ключ, до этого разделявший эти два узла. При этом в родительском узле может остаться только $t-2$ $t-2$ ключей. Тогда, если это не корень, мы выполняем аналогичную процедуру с ним. Если мы в результате дошли до корня, и в нём осталось от 1 до $t-1$ $t-1$ ключей, делать ничего не надо, потому что корень может иметь и меньше $t-1$ $t-1$ ключей. Если же в корне не осталось ни одного ключа, исключаем корневой узел, а его единственный потомок делаем новым корнем дерева.

Если $x$ $x$ — не лист, а K — его $i$ $i$ -й ключ, удаляем самый правый ключ из поддерева потомков $i$ $i$ -го потомка $x$ $x$ , или, наоборот, самый левый ключ из поддерева потомков $i+1$ $i+1$ -го потомка $x$ $x$ . После этого заменяем ключ K удалённым ключом. Удаление ключа происходит так, как описано в предыдущем абзаце.

Основные достоинства

Во всех случаях полезное использование пространства вторичной памяти составляет свыше 50 %. С ростом степени полезного использования памяти не происходит снижения качества обслуживания.
Произвольный доступ к записи реализуется посредством малого количества подопераций (обращения к физическим блокам).
В среднем достаточно эффективно реализуются операции включения и удаления записей; при этом сохраняется естественный порядок ключей с целью последовательной обработки, а также соответствующий баланс дерева для обеспечения быстрой произвольной выборки.
Неизменная упорядоченность по ключу обеспечивает возможность эффективной пакетной обработки.

Основной недостаток В-деревьев состоит в отсутствии для них эффективных средств выборки данных (то есть метода обхода дерева), упорядоченных по свойству, отличному от выбранного ключа.

См. также

Поиск в глубину
Поиск в ширину
Сбалансированные (самобалансирующиеся) деревья:

Список структур данных (деревья)

Примечания

Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Глава 18. B-деревья // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М. : , 2006. — С. 515—536. — ISBN 0-07-013151-1 .

Литература

Глава 7. Пространственно-временной компромисс: B-деревья // — М. : , 2006. — С. 331—339. — 576 с. — ISBN 978-5-8459-0987-9
Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Глава 18. B-деревья // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М. : , 2006. — С. 515—536. — ISBN 0-07-013151-1 .

Ссылки

видео:

[cormen-1] Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Глава 18. B-деревья // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М. : , 2006. — С. 515—536. — ISBN 0-07-013151-1 .