Interested Article - Формула Брахмагупты

- 2020-05-28
- 1
Фо́рмула Брахмагу́пты — обобщение формулы Герона , выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон.
Формулировка
Если вписанный четырёхугольник имеет длины сторон и полупериметр , то его площадь выражается формулой:

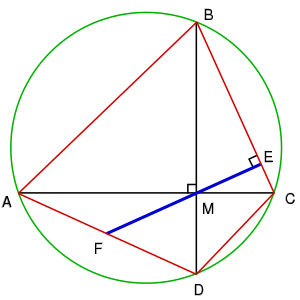
Площадь вписанного в окружность четырехугольника равна сумме площадей и
Так как является вписанным четырехугольником, то Следовательно, :
Записав теорему косинусов для стороны в и получаем:
Используем ( и противолежащие), а затем выносим за скобки :
Подставим полученное в полученную ранее формулу площади:
Применим формулу :
Так как полупериметр
Извлекая квадратный корень, получаем:
Вариации и обобщения
- Формула Брахмагупты обобщает формулу Герона для площади треугольника : достаточно считать, что длина одной из сторон равна нулю (например, ).
-
На случай произвольных четырёхугольников
формула Брахмагупты
может быть обобщена следующим образом:
- где есть полусумма противоположных углов четырёхугольника. (Какую именно пару противоположных углов взять, роли не играет, так как если полусумма одной пары противоположных углов равна , то полусумма двух других углов будет , и )
- Иногда эту более общую формулу записывают так:
- где и — длины диагоналей четырёхугольника.
-
Если четырёхугольник описанный, тогда
, и обобщённая формула Брахмагупты даёт
- .
-
В частности, для вписанно-описанных четырёхугольников
- .
-
доказал, что для любого вписанного многоугольника с
сторонами величина
является корнем некоторого многочлена
, коэффициенты которого в свою очередь являются многочленами от длин сторон. Он нашёл эти многочлены для
и
. Другими авторами установлено, что многочлен
можно выбрать так, чтобы его старший коэффициент был равен единице, а степень
была равна
, если
и
, если
. Здесь
- где — биномиальные коэффициенты . Для многоугольников с небольшим числом сторон имеем , , , (последовательность в OEIS ) и , , , (последовательность в OEIS ).
- Если в формуле Брахмагупты выразить полупериметр через полусумму всех сторон данного четырехугольника, возвести обе части в квадрат, умножить на -16, раскрыть скобки и привести подобные, то она примет вид:
- Правая часть совпадает с разложением определителя, приведенного ниже, если его умножить на -1. Поэтому можно написать, что
- Есть модификация формулы Брахмагупты для геометрии Лобачевского
См. также
Примечания
- , с. 37—39.
- Медных А. Д. О формуле Брахмагупты в геометрии Лобачевского. Математическое просвещение 2012. Выпуск 16. С. 172–180//
Популярная литература
- А. Ю. Давидов . . — 1863.
- В. В. Прасолов . Формула Брахмагупты // Математика в школе . — 1991. — № 5 .
- Коксетер Г. С. М. , Грейтцер С. П. . — М. : Наука , 1978. — Т. 14. — ( Библиотека математического кружка ).
Научная литература
- В. В. Варфоломеев. // Мат. сборник. . — 2003. — Т. 194 , № 3 . — С. 3—24 .
- Стариков В. Н. Заметки по геометрии // Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов / Гл. ред. Романова И. В.. — Чебоксары: ЦДИП «INet», 2014. — Вып. 1 . — С. 37-39 .
- M. Fedorchuk, I. Pak . (англ.) // : journal. — 2005. — Vol. 129 , no. 2 . — P. 371—404 . — doi : .
- 2020-05-28
- 1