Квантовый компьютер
- 1 year ago
- 0
- 0

Ква́нтовый компью́тер — вычислительное устройство , которое использует явления квантовой механики ( квантовая суперпозиция , квантовая запутанность ) для передачи и обработки данных. Квантовый компьютер (в отличие от обычного) оперирует не битами (способными принимать значение либо 0, либо 1), а кубитами , имеющими значения одновременно и 0, и 1. Теоретически это позволяет обрабатывать все возможные состояния одновременно, достигая существенного преимущества ( квантового превосходства ) над обычными компьютерами в ряде алгоритмов .
Полноценный универсальный квантовый компьютер является пока гипотетическим устройством, сама возможность построения которого связана с серьёзным развитием квантовой теории в области многих частиц и сложных экспериментов; разработки в данной области связаны с новейшими открытиями и достижениями современной физики . На начало 2020-х годов практически были реализованы лишь единичные экспериментальные системы, исполняющие фиксированные алгоритмы небольшой сложности.
Первым практическим высокоуровневым языком программирования для такого вида компьютеров считается язык (англ.) (, основанный на Haskell (см. Квантовое программирование ).
История квантовых вычислений началась в начале 1980-х годов, когда физик Пол Бениофф предложил квантово-механическую модель машины Тьюринга в 1980 году.
Идея о квантовых вычислениях также была высказана Юрием Маниным в 1980 году .
Одна из первых моделей квантового компьютера была предложена Ричардом Фейнманом в 1981 году. Вскоре Пол Бениофф описал теоретические основы построения такого компьютера .
Также концепцию квантового компьютера в 1983 году предлагал в статье, которую он пытался опубликовать в течение более десяти лет до этого .
Необходимость в квантовом компьютере возникает тогда, когда мы пытаемся исследовать методами физики сложные многочастичные системы, подобные биологическим. Пространство квантовых состояний таких систем растёт как экспонента от числа составляющих их реальных частиц, что делает невозможным моделирование их поведения на классических компьютерах уже для . Поэтому Визнер и Фейнман высказали идею построения квантового компьютера.
Квантовый компьютер использует для вычисления не обычные (классические) алгоритмы, а процессы квантовой природы, так называемые квантовые алгоритмы , использующие квантовомеханические эффекты, — такие как квантовый параллелизм и квантовая запутанность .
Если классический процессор в каждый момент может находиться ровно в одном из состояний ( обозначения Дирака ), то квантовый процессор в каждый момент находится одновременно во всех этих базисных состояниях, при этом в каждом состоянии — со своей комплексной амплитудой . Это квантовое состояние называется « квантовой суперпозицией » данных классических состояний и обозначается как
Базисные состояния могут иметь и более сложный вид. Тогда квантовую суперпозицию можно проиллюстрировать, например, так: «Вообразите атом, который мог бы подвергнуться радиоактивному распаду в определённый промежуток времени. Или не подвергнуться. Мы можем ожидать, что у этого атома есть только два возможных состояния: „распад“ и „нераспад“, <…> но в квантовой механике у атома может быть некое объединённое состояние — „распада — нераспада“, то есть ни то, ни другое, а между. Вот это состояние и называется „суперпозицией“» .
Квантовое состояние может изменяться во времени двумя принципиально различными путями:
Если классические состояния есть пространственные положения группы электронов в квантовых точках , управляемых внешним полем , то унитарная операция есть решение уравнения Шрёдингера для этого потенциала.
Измерение есть случайная величина, принимающая значения с вероятностями соответственно. В этом состоит квантовомеханическое правило Борна . Измерение есть единственная возможность получения информации о квантовом состоянии, так как значения нам непосредственно недоступны. Измерение квантового состояния не может быть сведено к унитарной шрёдингеровской эволюции, так как, в отличие от последней, оно необратимо. При измерении происходит так называемый коллапс волновой функции , физическая природа которого до конца не ясна. Спонтанные вредоносные измерения состояния в ходе вычисления ведут к декогерентности, то есть отклонению от унитарной эволюции, что является главным препятствием при построении квантового компьютера (см.).
Квантовое вычисление есть контролируемая классическим управляющим компьютером последовательность унитарных операций простого вида (над одним, двумя или тремя кубитами ). В конце вычисления состояние квантового процессора измеряется, что и даёт искомый результат вычисления.
Содержание понятия «квантовый параллелизм» в вычислении может быть раскрыто так: «Данные в процессе вычислений представляют собой квантовую информацию, которая по окончании процесса преобразуется в классическую путём измерения конечного состояния квантового регистра. Выигрыш в квантовых алгоритмах достигается за счёт того, что при применении одной квантовой операции большое число коэффициентов суперпозиции квантовых состояний, которые в виртуальной форме содержат классическую информацию, преобразуется одновременно» .
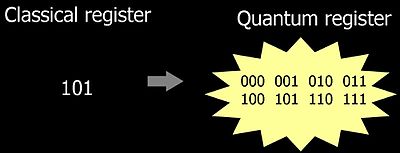
Идея квантовых вычислений состоит в том, что квантовая система из L двухуровневых квантовых элементов (квантовых битов, кубитов ) имеет 2 L линейно независимых состояний, а значит, вследствие принципа квантовой суперпозиции , пространство состояний такого квантового регистра является 2 L -мерным гильбертовым пространством . Операция в квантовых вычислениях соответствует повороту вектора состояния регистра в этом пространстве. Таким образом, квантовое вычислительное устройство размером L кубитов фактически задействует одновременно 2 L классических состояний.
Физическими системами, реализующими кубиты, могут быть любые объекты, имеющие два квантовых состояния: поляризационные состояния фотонов , электронные состояния изолированных атомов или ионов , спиновые состояния ядер атомов, и так далее.
Один классический бит может находиться в одном и только в одном из состояний или . Квантовый бит, называемый кубитом, находится в состоянии , так что | a |² и | b |² — вероятности получить 0 или 1 соответственно при измерении этого состояния; ; | a |² + | b |² = 1. Сразу после измерения кубит переходит в базовое квантовое состояние, соответствующее классическому результату.
Пример:
| 0 | составляет | (4/5)² = 16/25 | = 0,64, |
| 1 | составляет | (−3/5)² = 9/25 | = 0,36. |
Пример из квантовой механики: фотон находится в состоянии суперпозиции двух поляризаций. Это состояние есть вектор в двумерной плоскости, систему координат в которой можно представлять как две перпендикулярные оси, так что и есть проекции на эти оси; измерение раз и навсегда коллапсирует состояние фотона в одно из состояний или , причём вероятность коллапса равна квадрату соответствующей проекции. Полная вероятность получается по теореме Пифагора . При переходе к системе из двух кубитов, измерение каждого из них может дать 0 или 1. Поэтому у системы есть 4 классических состояния: 00, 01, 10 и 11. Аналогичные им базовые квантовые состояния: . И наконец, общее квантовое состояние системы имеет вид . Теперь | a |² — вероятность измерить 00 и т. д. Отметим, что | a |² + | b |² + | c |² + | d |² = 1 как полная вероятность.
Если измерить только первый кубит квантовой системы, находящейся в состоянии , получится:
В первом случае измерение даст состояние , во втором — состояние .
Результат такого измерения невозможно записать как вектор в гильбертовом пространстве состояний. Такое состояние, в котором участвует наше незнание о том, какой же результат получится на первом кубите, называют смешанным состоянием . В нашем случае такое смешанное состояние называют проекцией исходного состояния на второй кубит и записывают в виде матрицы плотности вида , где матрица плотности состояния определяется как .
В общем случае у системы из L кубитов существует 2 L классических состояний (00000… ( L нулей), …00001 ( L цифр), … , 11111… ( L единиц)), каждое из которых может быть измерено с вероятностями 0—1.
Таким образом, одна операция над группой кубитов вычисляется сразу над всеми возможными её значениями, в отличие от группы классических битов, когда может быть использовано лишь одно текущее значение. Это и обеспечивает беспрецедентный параллелизм вычислений.
Упрощённая схема вычисления на квантовом компьютере выглядит так: берётся система кубитов , на которой записывается начальное состояние. Затем состояние системы или её подсистем изменяется посредством унитарных преобразований , выполняющих те или иные логические операции . В конце измеряется значение, и это результат работы компьютера. Роль проводов классического компьютера играют кубиты , а роль логических блоков классического компьютера играют унитарные преобразования . Такая концепция квантового процессора и квантовых логических вентилей была предложена в 1989 году Дэвидом Дойчем . Также Дэвид Дойч в 1995 году нашёл универсальный логический блок, с помощью которого можно выполнять любые квантовые вычисления.
Оказывается, что для построения любого вычисления достаточно двух базовых операций. Квантовая система даёт результат, только с некоторой вероятностью являющийся правильным. Но за счёт небольшого увеличения операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице.
С помощью базовых квантовых операций можно симулировать работу обычных логических элементов, из которых сделаны обычные компьютеры. Поэтому любую задачу, которая решена сейчас, любой квантовый компьютер решит, и почти за такое же время .
Большая часть современных ЭВМ работают по такой же схеме: n битов памяти хранят состояние и каждый такт времени изменяются процессором. В квантовом случае система из n кубитов находится в состоянии, являющемся суперпозицией всех базовых состояний, поэтому изменение системы касается всех 2 n базовых состояний одновременно. Теоретически новая схема может работать намного (в экспоненциальное число раз) быстрее классической. Практически, например, квантовый алгоритм Гровера поиска в базе данных показывает квадратичный прирост мощности против классических алгоритмов.
Основные квантовые алгоритмы:
Было показано, что не для всякого алгоритма возможно «квантовое ускорение». Более того, возможность получения квантового ускорения для произвольного классического алгоритма является большой редкостью .
Любая квантовая операция может быть реализована при помощи логического вентиля «контролируемое отрицание» ( CNOT ) и поворота состояния одного кубита .
Один кубит можно представить в виде электрона в двухъямном потенциале, так что означает нахождение его в левой яме, а — в правой. Это называется кубит на зарядовых состояниях. Общий вид квантового состояния такого электрона: . Зависимость его от времени есть зависимость от времени амплитуд ; она задаётся уравнением Шрёдингера вида , где гамильтониан имеет в силу одинакового вида ям и эрмитовости вид для некоторой константы , так что вектор есть собственный вектор этого гамильтониана с собственным значением 0 (так называемое основное состояние), а — собственный вектор со значением (первое возбуждённое состояние). Никаких других собственных состояний (с определённым значением энергии) здесь нет, так как наша задача двумерная.
Поскольку каждое состояние переходит за время в состояние , то для реализации операции NOT (перехода и наоборот достаточно просто подождать время . То есть операция NOT реализуется просто естественной квантовой эволюцией кубита при условии, что внешний потенциал задаёт двухъямную структуру; это делается с помощью технологии квантовых точек.
Для реализации CNOT надо расположить два кубита (то есть две пары ям) перпендикулярно друг другу и в каждой из них расположить по отдельному электрону. Тогда константа для первой (управляемой) пары ям будет зависеть от того, в каком состоянии находится электрон во второй (управляющей) паре ям: если ближе к первой, то будет больше, если дальше — меньше. Поэтому состояние электрона во второй паре определяет время совершения NOT в первой яме, что позволяет снова выбрать нужную длительность времени для реализации операции CNOT.
Эта схема очень приблизительная и идеализирована; реальные схемы сложнее, и их реализация представляет вызов экспериментальной физике.
Алгоритм телепортации реализует точный перенос состояния одного кубита (или системы) на другой. В простейшей схеме используются 3 кубита: телепортируемый кубит и запутанная пара , один кубит которой находится на другой стороне. Отметим, что в результате работы алгоритма первоначальное состояние источника разрушится — это пример действия общего принципа невозможности клонирования — невозможно создать точную копию квантового состояния, не разрушив оригинал. Не получится скопировать произвольное состояние, и телепортация — замена этой операции.
Телепортация позволяет передавать квантовое состояние системы с помощью обычных классических каналов связи. Таким образом можно, в частности, получить связанное состояние системы, состоящей из подсистем, удалённых на большое расстояние. Это позволяет построить системы связи, в принципе не поддающиеся прослушиванию (на отрезке между «квантовыми» устройствами).
Благодаря огромной скорости разложения на простые множители квантовый компьютер позволит расшифровывать сообщения, зашифрованные широко применяемым криптографическим алгоритмом RSA . До сих пор этот алгоритм считается сравнительно надёжным, так как эффективный способ разложения чисел на простые множители для классического компьютера в настоящее время неизвестен. Для того, например, чтобы получить доступ к кредитной карте [ прояснить ] , нужно разложить на два простых множителя число длиной в сотни цифр (даже для суперкомпьютеров выполнение этой задачи заняло бы в сотни раз больше времени, чем возраст Вселенной ). Благодаря квантовому алгоритму Шора эта задача становится вполне осуществимой, если квантовый компьютер будет построен. В связи с этим особую актуальность приобретают исследования по постквантовой криптографии — криптографическим алгоритмам, обеспечивающим конфиденциальность в условиях квантовых атак.
В конце декабря 2022 года была опубликована работа группы китайских учёных, которая продемонстрировала возможность взлома достаточно длинных RSA-ключей с помощью современных квантовых компьютеров. В работе рассказано о первом в истории взломе 48-битного ключа .
Применение идей квантовой механики уже открыло новую эпоху в области криптографии, так как методы квантовой криптографии открывают новые возможности в области передачи сообщений . Прототипы систем подобного рода находятся на стадии разработки .
Квантовое машинное обучение позволяет манипулировать большими объёмами данных за один проход и моделировать нейронную сеть экспоненциального размера . В 2013 году корпорация Google объявила об открытии лаборатории по квантовым исследованиям в области искусственного интеллекта . Концерн Volkswagen ведёт исследования в сфере применения квантовых компьютеров для разработки беспилотного автомобиля и новых типов аккумуляторных батарей (используя квантовые компьютеры Google и D-Wave ). В ноябре 2018 года концерн объявил о разработке системы управления дорожным движением (с интеграцией в неё беспилотных машин), работающей с использованием квантовых компьютеров D-Wave .
Предполагается, что с помощью квантовых компьютеров станет возможно точное моделирование молекулярных взаимодействий и химических реакций. Химические реакции являются квантовыми по своей природе. Для классических компьютеров доступен обсчёт поведения только относительно простых молекул . По прогнозам экспертов, моделирование на квантовых компьютерах открывает новые перспективы для развития химической отрасли , в частности при создании лекарств .
Построение квантового компьютера в виде реального физического прибора является фундаментальной задачей физики XXI века. По состоянию на начало 2018 года построены только ограниченные варианты квантового компьютера (самые большие сконструированные квантовые регистры имеют несколько десятков связанных кубитов ). Существуют скептические мнения о ряде перспектив квантовых вычислений:
Практическое осуществление квантового компьютера основано на манипулировании на микроскопическом уровне и с грандиозной точностью многоэлементной физической системой с непрерывными степенями свободы. Очевидно, что для достаточно большой системы, квантовой или классической, эта задача становится невыполнимой, именно поэтому такие системы переходит из ведения микроскопической физики в область статистической физики. Представляет ли система из N = 10 3 ÷10 5 квантовых спинов, необходимая чтобы превзойти классический компьютер в решении ограниченного числа специальных задач, достаточно большой в этом смысле? Сможем ли мы когда-либо научиться контролировать 10 300 (по меньшей мере) амплитуд, определяющих квантовое состояние такой системы? Мой ответ — нет, никогда .
— М. И. Дьяконов , «Будет ли у нас когда-нибудь квантовый компьютер?»
Главные технологии для квантового компьютера:
Основные проблемы, связанные с созданием и применением квантовых компьютеров:
Чем больше кубитов находятся в связанном состоянии, тем менее стабильной является система. Для достижения «квантового превосходства» требуется компьютер со многими десятками связанных кубитов, работающими стабильно и с малым числом ошибок. Вопрос о том, до какой степени возможно масштабирование такого устройства (так называемая «проблема масштабирования»), является предметом новой интенсивно развивающейся области — многочастичной квантовой механики . Центральным здесь является вопрос о природе декогерентности (точнее, о коллапсе волновой функции ), который пока остаётся открытым. Различные трактовки этого процесса можно найти в книгах .
На рубеже XX—XXI веков во многих научных лабораториях были созданы однокубитные квантовые процессоры (по существу, управляемые двухуровневые системы, в которых можно было предполагать возможность масштабирования на много кубитов).
В конце 2001 года IBM заявила об успешном тестировании 7-кубитного квантового компьютера, реализованного с помощью ядерного магнитного резонанса . На нём был исполнен алгоритм Шора и были найдены сомножители числа 15 .
В 2005 году группой Ю. Пашкина (кандидат физ.-мат. наук, старший научный сотрудник лаборатории сверхпроводимости г. Москвы) при помощи японских специалистов был построен двухкубитный квантовый процессор на сверхпроводящих элементах .
В ноябре 2009 года физикам из Национального института стандартов и технологий (США) впервые удалось собрать программируемый квантовый компьютер, состоящий из двух кубитов .
В феврале 2012 года компания IBM сообщила о достижении значительного прогресса в физической реализации квантовых вычислений с использованием сверхпроводящих кубитов, соединённых с кремниевыми микросхемами, что, по мнению компании, позволит начать работы по созданию квантового компьютера .
В апреле 2012 года группе исследователей из Южно-Калифорнийского университета , Технологического университета Дельфта , университета штата Айова , и Калифорнийского университета, Санта-Барбара , удалось построить двухкубитный квантовый компьютер на кристалле алмаза с примесями. Компьютер функционирует при комнатной температуре и теоретически является масштабируемым. В качестве двух логических кубитов использовались направления спина электрона и ядра азота соответственно. Для обеспечения защиты от влияния декогерентности была разработана целая система, которая формировала импульс микроволнового излучения определённой длительности и формы. При помощи этого компьютера реализован алгоритм Гровера для четырёх вариантов перебора, что позволило получить правильный ответ с первой попытки в 95 % случаев .
В июле 2017 года группа физиков под руководством Михаила Лукина , сооснователя Российского квантового центра и профессора Гарвардского университета, создала программируемый 51-кубитный квантовый симулятор . Это самая сложная подобная система из существующих на тот момент. Авторы проверили работоспособность симулятора моделированием сложной системы из множества частиц — это позволило физикам предсказать некоторые ранее неизвестные эффекты . Примерно в это же время другая группа учёных из университета Мэриленд под руководством создала 53-кубитный симулятор, основанный на ионах в оптической ловушке . Однако обе эти системы не являются универсальным компьютером, а созданы для решения одной задачи .
В ноябре 2017 года учёные IBM успешно построили и испытали прототип процессора с 50 кубитами .
В январе 2018 года исполнительный директор компании Intel Брайан Кржанич сообщил о создании сверхпроводящей квантовой микросхемы под кодовым именем «Tangle Lake», обладающей 49 кубитами. По его прогнозу, квантовые компьютеры помогут в создании лекарств, финансовом моделировании и составлении прогнозов погоды. Intel ведёт разработки квантовых компьютеров по двум направлениям: создание устройств на сверхпроводниках и кремниевых микросхемах со «спиновыми кубитами» .
В марте 2018 года компания Google объявила, что ей удалось построить 72-кубитный квантовый процессор , имеющий низкую вероятность ошибок в вычислениях. Компания не раскрыла подробных характеристик устройства, однако утверждает, что оно позволяет достичь «квантового превосходства». Согласно специалистам Google, для того чтобы квантовый компьютер мог решать задачи, недоступные для «обычных» компьютеров, требуется соблюдение следующих условий: в его состав должно входить не менее 49 кубитов, «глубина» ( англ. circuit depth) должна превышать 40 кубитов, а вероятность ошибки в двухкубитном логическом элементе должна быть не выше 0,5 %. Представители компании выразили надежду, что в будущем они смогут достигнуть этих показателей.
В декабре 2018 года сообщено о разработке оптического микрочипа, который в будущем запланировано использовать в качестве составной части квантового компьютера.
В январе 2019 года компания IBM представила первый в мире коммерческий квантовый компьютер IBM Q System One .
В октябре 2019 года компания Google объявила, что ей удалось построить 53-кубитный сверхпроводящий квантовый процессор Sycamore и продемонстрировать «квантовое превосходство» над обычными компьютерами .
В декабре 2020 года исследователи из Научно-технического университета Китая опубликовали статью, в которой утверждается, что их квантовый компьютер Цзючжан смог достичь квантового превосходства. Ему всего за несколько минут удалось провести операцию, которая традиционным способом решалась бы около двух миллиардов лет. Компьютер работает на основе оптических квантовых вычислителей (кубиты базируются на фотонах) с применением «бозонного семплинга».
В 2021 году группы китайских учёных под руководством создали два прототипа квантовых компьютеров:
В конце 2021 года компания IBM представила свой новый квантовый процессор на сверхпроводящих кубитах, получивший название Eagle («Орёл») , который является частью программы по созданию супербыстрых компьютеров. У нового чипа 127 кубитов, что в два раза превышает предыдущие квантовые процессоры IBM .
В ноябре 2022 года компания IBM представила свой новый квантовый процессор Osprey, c 433 кубитами, который будет использовать компьютер IBM Quantum System Two.
Канадская компания D-Wave Systems с 2007 года заявляла о создании различных вариантов квантового компьютера: от 16-кубитного до 2000-кубитного. Компьютеры D-Wave пригодны для решения лишь узкого класса задач. Некоторые исследователи высказывали сомнения, что в компьютерах компании действительно достигается существенное «квантовое ускорение», однако компьютеры D-Wave (предлагаемые по ценам 10—15 млн USD ) покупались компаниями Google , Lockheed Martin и , а также агентством NASA и Лос-Аламосской национальной лабораторией .
В декабре 2015 года специалисты компании Google подтвердили, что, согласно их исследованию, компьютер D-Wave использует квантовые эффекты. При этом в «1000-кубитном» компьютере кубиты в действительности организованы в кластеры по 8 кубитов каждый. Тем не менее это позволило добиться быстродействия в 100 млн раз больше (по сравнению с обычным компьютером) в одном из алгоритмов.
В феврале 2022 года Исследовательский центр Юлиха в Германии запустил квантовый суперкомпьютер с более чем 5000 кубитов. Компьютер был создан на базе канадской системы D-Wave с удалённым облачным доступом. Эта квантовая разработка предназначена для решения задач оптимизации и выборки. Чтобы реализовать коммерческое применение квантовых вычислений, германский центр создал Юлихскую пользовательскую инфраструктуру для квантовых вычислений (JUNIQ), чтобы обеспечить доступ к такого рода вычислениям различным группам пользователей и компаний в Европе.