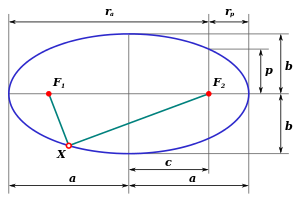
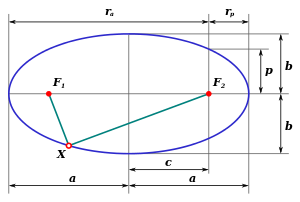
Э́ллипс рассе́ивания — условная замкнутая кривая, описанная вокруг точек падения снарядов, выпущенных из одного орудия в максимально возможных одинаковых условиях.

Разброс точки попадания вызывается рассеиванием снарядов и в общем случае подчиняется закону нормального распределения .

Причины возникновения эллипса рассеивания

Так как невозможно обеспечить абсолютно одинаковые условия стрельбы (всегда присутствуют небольшие отклонения в весе и составе метательного заряда , форме и весе снаряда , изменения метеоусловий, отклонение ствола орудия в момент выстрела и т. п.) происходит рассеивание точек попадания. Этот факт хорошо известен и даже нашёл своё отражение в фольклоре в устойчивом выражении «снаряд два раза в одну воронку не попадает».

В общем случае все факторы, вызывающие рассеивание, носят случайный характер и взаимно независимы, и результат их воздействия подчиняется нормальному распределению случайных величин согласно центральной предельной теоремой теории вероятностей. Полностью исключить влияние всех этих факторов рассеивания невозможно. Неизбежное рассеивание снарядов хорошо изучено и статистически описано. В артиллерии такое описание известно как эллипс рассеивания.

Каждый снаряд, выпущенный в приблизительно равных условиях, движется по своей траектории , составляя при серии выстрелов так называемый «сноп траекторий». Точки падения снарядов из снопа траекторий некоторым образом распределяются вокруг некоего центра рассеивания снарядов. При рассмотрении результатов подобного рассеивания выделяются 3 момента:

• ширина рассеивания не беспредельна, она имеет свои границы;
• рассеивание симметрично относительно своего центра: перелёты-недолёты и отклонения вправо-влево встречаются одинаково часто;
• рассеивание неравномерно, вблизи центра плотность точек попадания выше, чем на границах.

Исходя из этих трёх положений формально определяется эллипс рассеивания.

Закономерности эллипса рассеивания

Внутри эллипса рассеивания различают несколько областей, вероятность попадания снаряда в которые имеет своё численное значение. Основной характеристикой этих областей служит вероятное (срединное) отклонение . Под этим термином понимают половину длины участка, симметрично расположенного относительно центра рассеивания, вероятность попадания в который равна 50 %.

Различают вероятные отклонения по дальности (Вд) , по направлению (Вб) , по высоте (Вв) . Данные величины рассчитаны для каждой траектории и указаны в таблицах стрельбы .

Таким образом, вероятность попадания в полосу, находящуюся на удалении в одно срединное отклонение от центра в том или ином направлении, составляет 25 %. Практически в артиллерии границы эллипса рассеивания принимают равными четырём вероятным отклонениям в каждую сторону от центра рассеивания. Вычислено, что вероятность попадания в полосу от одного до двух вероятных отклонений — 16 %, от двух до трёх — 7 %, свыше трёх — 2 %. Эта закономерность верна для всех отклонений: по дальности, по направлению, по высоте. На небольших дальностях стрельбы эллипс рассеивания их-за настильности траектории снарядов имеет ярко выраженную вытянутую форму в направлении стрельбы, а по мере увеличения дальности приближается по форме к окружности и может даже вытягиваться поперёк направления стрельбы (то есть Вб растёт сильнее, чем Вд ).

Закономерности эллипса рассеивания используются при пристрелке и корректировке артиллерийского огня. Например, если при серии из четырёх выстрелов наблюдается один перелёт и три недолёта (то есть процент недолётов — 75 %), то это значит, что центр попаданий смещён относительно цели на 1 Вд . Отсюда следует, что необходимо увеличить дальность стрельбы на величину, равную 1 Вд .

См. также

• Круговое вероятное отклонение
• Кучность боя оружия
• Средняя точка попадания

Литература

• Левченко В. А., Сергин М. Ю., Иванов В. А., Зеленин Г. В. Глава 3. Рассеивание снарядов при ударной стрельбе // . — Тамбов: Издательство ТГТУ, 2004. — 268 с. — ISBN 5-8265-0114-6 . от 28 января 2007 на Wayback Machine
• Арсеньев В. Н., Булекбаев Д. А. . — журнал Приборостроение СНИУ ИТМО. — январь 2014. — Статья. — УДК 629.191. — стр. 5—10