Interested Article - Reservoir sampling

Reservoir sampling («резервуарная выборка», нет устоявшегося русского перевода) представляет собой семейство вероятностных алгоритмов произвольного выбора образца , состоящего из k элементов из списка S , содержащего n элементов, где n — это либо очень большое, либо неизвестное число. Обычно, n достаточно велико, чтобы весь список не уместился в основной памяти .

Пример: выборка размера 1

Предположим, мы видим последовательность элементов, но по одному элементу за 1 раз. Мы хотим сохранить один элемент в памяти, и мы хотим, чтобы он был выбран случайным образом из данной последовательности. Если мы знаем общее количество элементов ( n ), то есть простое решение: выбрать индекс i между 1 и n с равной вероятностью, и выбрать i -ый элемент. Проблема заключается в том, что мы не всегда знаем n заранее. Возможное решение заключается в следующем:

Сохранить первый элемент в памяти.
Когда получим $i$ $i$ -й элемент (для $i>1$ $i>1$ ):
- с вероятностью $1/i$ сохранить новый элемент вместо текущего элемента;
- с вероятностью $1-1/i$ сохранить текущий элемент и отбросить новый элемент.

Итак:

когда есть только один элемент, он сохранится с вероятностью 1;
когда есть 2 элемента, каждый из них сохранится с вероятностью 1/2;
когда есть 3 элемента, третий элемент сохранится с вероятностью 1/3, а каждый из предыдущих 2 пунктов также сохранится с вероятностью (1/2)(1-1/3) = (1/2)(2/3) = 1/3;
по индукции легко доказать, что при наличии n элементов, каждый элемент сохранится с вероятностью 1/ n .

Алгоритм R

В своей статье на эту тему наиболее распространенный пример Джеффри Виттер назвал алгоритмом R . Этот простой O( n ) алгоритм, как описано в Dictionary of Algorithms and Data Structures состоит из следующих шагов (при условии, что массивы начинаются с индекса 1, а количество элементов, которые нужно выбрать, k , меньше, чем размер исходного массива, S ):

/*
  S has items to sample, R will contain the result
*/
ReservoirSample(S[1..n], R[1..k])
  // fill the reservoir array
  for i = 1 to k
      R[i] := S[i]

  // replace elements with gradually decreasing probability
  for i = k+1 to n
    j := random(1, i)   // important: inclusive range
    if j <= k
        R[j] := S[i]

Алгоритм создаёт «резервуар» — массив размера k — и заполняет его первыми k элементами из S . Затем он перебирает все оставшиеся элементы S , пока S не будет исчерпан. На i -ом элементе S алгоритм генерирует случайное число j между 1 и i . Если j меньше или равно k , то j -ый элемент резервуара заменяется на i -й элемент из S . В сущности, для всех i , i -ый элемент S выбирается для включения в резервуар с вероятностью k/i . Аналогичным образом, на каждой итерации j -й элемент резервуара будет заменён с вероятностью 1/k * k/i , то есть, упрощая, с вероятностью 1/i . Можно показать, что, когда алгоритм закончит свою работу, каждый элемент в S имеет одинаковую вероятность (то есть k / длина(S) ), что его выберут в резервуар. Чтобы убедиться в этом, рассмотрим следующее доказательство по индукции . После (i-1) -го шага, допустим, вероятность числа попасть в резервуар равна k/(i-1) . Поскольку вероятность числа быть заменены на i -ом шаге равна 1/i , то вероятность того, что он выживает на i-ом шаге, равна (i-1)/i . Таким образом, вероятность того, что заданное число попадёт в резервуар после i -го шага, равна произведению этих двух вероятностей, то есть вероятности уже находиться в резервуаре после (i-1) -го шага и вероятности пережить замену на i-ом шаге. Это произведение равно: (k/(i-1)) * ((i-1)/i) = k/i . Следовательно, результат зависит от i , и поэтому утверждение верно по индукции.

Резервуар со случайной сортировкой

Простой алгоритм на основе резервуара может быть разработан с использованием случайной сортировки и реализован с использованием структуры данных приоритетная очередь. Этот алгоритм присваивает случайное число в качестве ключа к каждому элементу и поддерживает k элементов с минимальным значением для ключей. В сущности, это эквивалентно присвоению случайного числа каждому элементу в качестве ключа, последующей сортировке элементов с помощью этих ключей и выборки первых k элементов. В худшем случае время выполнения алгоритма равно $O(n\log k)$ , а в лучшем случае — $O(n)$ . Хотя наихудший случай по времени не так хорош, как Алгоритм R, этот алгоритм может быть легко расширен для взвешенной выборки. Оба алгоритма могут работать на потоках неизвестной длины

.
/*
  S is a stream of items to sample, R will contain the result
  S.Current returns current item in stream
  S.Next advances stream to next position
  max-priority-queue supports:
    Count -> number of items in priority queue
    Maximum() -> returns maximum key value of all items
    Extract-Max() -> Remove the item with max key
    Insert(key, Item) -> Adds item with specified key
*/
ReservoirSample(S[1..?], R[1..k])
  H = new max-priority-queue
  while S has data
    r = Random(0,1)  // important: inclusive range
    if H.Count < k
      H.Insert(r, S.Current)
    else
      if H.Maximum > r
        H.Extract-Max()
        H.Insert(r, S.Current)
    S.Next

Взвешенная случайная выборка с использованием резервуара

Во многих приложениях выборки требуется производить в соответствии с весами, которые присвоены каждому элементу в данном множестве. Например, это может потребоваться для выборки запросов в поисковой машине с весом как количеством раз, когда они были выполнены, так что образец мог бы быть проанализирован на общее воздействие на пользовательский опыт. Есть два способа интерпретировать веса каждого элемента множества:

Пусть вес каждого пункта $w_{i}$ , а сумма всех весов $W$ . Мы можем преобразовать вес в вероятность выбора элемента в качестве образца так: $P_{i}=w_{i}/W$ .
Пусть веса двух элементов $i$ и $j$ будут $w_{i}$ и $w_{j}$ . Пусть вероятность элемент $i$ стать выбранным в качестве образца будет $p_{i}$ , тогда $p_{j}=p_{i}\max(1,w_{j}/w_{i})$ .

Алгоритм A-Res

Следующий алгоритм предложили Efraimidis и Spirakis, в нём используется интерпретация 1:

/*
  S is a stream of items to sample, R will contain the result
  S.Current returns current item in stream
  S.Weight  returns weight of current item in stream
  S.Next advances stream to next position
  The power operator is represented by ^
  min-priority-queue supports:
    Count -> number of items in priority queue
    Minimum() -> returns minimum key value of all items
    Extract-Min() -> Remove the item with minimum key
    Insert(key, Item) -> Adds item with specified key
*/
ReservoirSample(S[1..?], R[1..k])
  H = new min-priority-queue
  while S has data
    r = Random(0,1) ^ (1/S.Weight)  // important: inclusive range
    if H.Count < k
      H.Insert(r, S.Current)
    else
      if H.Minimum < r
        H.Extract-Min()
        H.Insert(r, S.Current)
    S.Next

Этот алгоритм совпадает с алгоритмом, приведенным в , за исключением строки, где мы генерируем ключ, используя генератор случайных чисел. Алгоритм эквивалентен назначению каждому элементу в качестве ключа $r^{1/w_{i}}$ , в котором $r$ — случайное число, а затем сортировке элементов с использованием этих ключей и, наконец, выборке первых k элементов для образца.

Алгоритм A-Chao

Следующий алгоритм, предложенный M. T. Chao, использует интерпретацию 2:

/*
  S has items to sample, R will contain the result
  S[i].Weight contains weight for each item
*/
WeightedReservoir-Chao(S[1..n], R[1..k])
  WSum = 0
  // fill the reservoir array
  for i = 1 to k
      R[i] := S[i]
      WSum = WSum + S[i].Weight
  for i = k+1 to n
    WSum = WSum + S[i].Weight
    p = S[i].Weight / WSum // probability for this item
    j := random(0, 1);     // important: inclusive range
    if j <= p              // select item according to probability
        R[random(1,k)] := S[i]  //uniform selection in reservoir for replacement

Для каждого элемента вычисляет его относительный вес, а затем используется для случайного решения, нужно ли такой элемент добавить в резервуар. Если элемент выбран, то один из существующих элементов резервуара равномерно выбирается и заменяется на новый элемент. Трюк здесь заключается в том, что, если вероятности всех элементов в резервуаре уже пропорциональны их весам, то, выбрав равномерно, какой элемент необходимо заменить, вероятности всех элементов остаются пропорциональными их весу после замены.

Распределённая резервуарная выборка

Во многих приложениях, объем данных, из которых необходим небольшой образец, слишком велик, и желательно распределить задачи выбора среди многих машин параллельно, чтобы ускорить процесс. Простой подход, который часто используется, хотя он и менее производителен, заключается в том, чтобы присвоить случайное число в качестве ключа каждому элементу, затем выполнить распределенную сортировки и, наконец, получить образец нужного размера из первых k элементов. Если взвешенный образец подходит, тогда ключ вычисляется с использованием $r^{1/w_{i}}$ , где $r$ — случайное число, а $w_{i}$ — вес элемента. Неэффективность этого подхода с очевидностью вытекает из требуемой распределенной сортировки очень больших объемов данных.

Другой, более эффективный подход для распределенной взвешенной случайной выборки заключается в следующем:

Распределить данные среди m машин.
Каждая машина производит свою собственную взвешенную выборку с использованием ключа $r^{1/w_{i}}$ , как описано в предыдущем разделе, и производит выборку размером <= k элементов.
Собрать все m образцов размером <= k, получив в итоге общее количество элементов $n'<=mk$ .
Теперь выбрать k элементов из $n'$ элементов из шага 3, используя ключ, который уже был вычислен в шаге 2. Это означает, что вместо повторной генерации ключа с использованием генератора случайных чисел в алгоритме выборки, мы используем ключ, который у нас уже вычислен на шаге 2.

Шаг 4 использует ключи из шага 2, потому что мы можем иметь несбалансированное распределение данных по машинам. Например, предположим, что k = 1, машина m1 машина получает только 1 элемент с весом 10, а машина m2 получает 2 элемента, каждый с весом 100. Интуитивно, вероятность элементов из m1 попасть в финальную выборку равна 1/210. В шаге 3, мы получим 1 элемент из m1, как из m2. Если мы пересчитываем ключи в шаге 4, то вероятность того, что элемент из m1 будет в окончательной выборке, составляет 10/110 вместо требуемых 1/210. Теперь заметим, что взвешенная случайная выборка из предыдущего раздела уменьшает максимальное значение ключа в приоритетной очереди по мере обработки всё большего количества элементов. Поэтому, элементы, выбранный на машине с более крупным куском данных, будут иметь низкие значения ключа и, следовательно, более высокий шанс попасть в выборку.

Отношение к тасованию Фишера-Йетса

Предположим, кто-то хотел раздать k случайных карт из колоды игральных карт (то есть n=52 ). Естественным подходом было бы перетасовать колоду и затем взять первые k карт.

В общем случае, перемешивание тоже должно работать, даже если количество карт в колоде заранее не известно, условие которого удовлетворяется вывернутой наизнанку версией тасования Фишер-Йетса :

Чтобы инициализировать массив a из n элементов как случайно перемешанной копии S , индексы обоих массивов начинаются с 0: a [0] ← S [0] for i from 1 to n - 1 do r ← random (0 .. i ) a [ i ] ← a [ r ] a [ r ] ← S [ i ]

Обратите внимание, что хотя остальные карты тасуются, только первые k важны в данном контексте.

Поэтому, массиву a нужно отслеживать только карты в первых k позициях при выполнении перемешивания, уменьшив объем необходимой памяти.

Усекая a до длины k , алгоритм модифицируется соответствующим образом:

Чтобы инициализировать массив a в k случайных элементов из S (длиной n ), индексы обоих массивов начинаются с 0: a [0] ← S [0] for i from 1 to k - 1 do r ← random (0 .. i ) a [ i ] ← a [ r ] a [ r ] ← S [ i ]

for i from k to n - 1 do r ← random (0 .. i ) if ( r < k ) then a [ r ] ← S [ i ]

Так как порядок первых k карт является несущественным, первый цикл может быть удалён, а массив a может быть инициализирован первыми k элементами из S .

Это напоминает алгоритм R .

Пример реализации

Ниже приводится простая реализация алгоритма на языке Python , которая выбирает названия страниц из английской Википедии:

import random
SAMPLE_COUNT = 10

# Force the value of the seed so the results are repeatable
random.seed(12345)

sample_titles = []
for index, line in enumerate(open("enwiki-20091103-all-titles-in-ns0")):
        # Generate the reservoir
        if index < SAMPLE_COUNT:
                sample_titles.append(line)
        else:
                # Randomly replace elements in the reservoir
                # with a decreasing probability.
                # Choose an integer between 0 and index (inclusive)
                r = random.randint(0, index)
                if r < SAMPLE_COUNT:
                        sample_titles[r] = line
print sample_titles

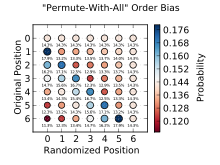
Статистические свойства

Вероятности выбора резервуарных методов обсуждаются в Chao (1982) и Tillé (2006). Если во время первого отбора вероятности равны k/n (или, в случае процедуры Chao, произвольному множеству неравных вероятностей), то во время второго отбора вероятности зависят от порядка, в котором записи отсортированы в оригинальном резервуаре. Проблема преодолевается кубическим методом выборки Deville and Tillé (2004).

Ограничения

Резервуарные выборки делают предположение, что результат помещается в основной памяти , часто подразумевая, что k является постоянной, не зависящей от n . В применениях, где мы хотели бы выбрать большое подмножество входного списка (скажем, треть, то есть k=n/3 ), нужно использовать другие методы. Были предложены распределенные реализации этой задачи.

См. также

Ссылки

Vitter, Jeffrey S. (неопр.) // (англ.) ( . — 1985. — 1 March ( т. 11 , № 1 ). — С. 37—57 . — doi : .
. Дата обращения: 19 декабря 2015. 8 октября 2015 года.
Sunter, A. B. List Sequential Sampling with Equal or Unequal Probabilities without Replacement (англ.) // Applied Statistics : journal. — 1977. — Vol. 26 , no. 3 . — P. 261 . — doi : .
↑ Efraimidis, Pavlos S.; Spirakis, Paul G. (неопр.) // (англ.) ( . — 2006. — 16 March ( т. 97 , № 5 ). — С. 181—185 . — doi : .
↑ Дата обращения: 19 декабря 2015. 10 сентября 2013 года.
. gregable.com . Дата обращения: 23 июля 2015. 23 июля 2015 года.
Дата обращения: 29 сентября 2017. 5 марта 2016 года.
Дата обращения: 19 декабря 2015. 14 августа 2013 года.
. Дата обращения: 19 декабря 2015. 22 декабря 2015 года.