Теория колебаний — раздел математики, в котором рассматриваются всевозможные колебания , абстрагируясь от их физической природы . Для этого используется аппарат дифференциальных уравнений .

Гармонические колебания

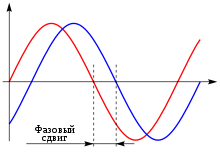
Гармонические колебания — это такие колебания, при которых колеблющаяся величина (например, отклонения маятника) изменяется со временем по закону синуса или косинуса :

${\displaystyle x(t)=A\cos(\omega t+\varphi )}$

Гармонические колебания с затуханием

Гармонические колебания с затуханием — это такие колебания, при которых колеблющаяся величина (например, отклонения маятника) изменяется со временем, как произведение синуса (косинуса) на убывающую экспоненту .

${\displaystyle x(t)=Ae^{-kt}\cos(\omega t+\varphi )}$

Параметрические колебания

Параметрические колебания происходят когда один из параметров системы (коэффициент дифференциального уравнения колебаний) изменяется периодически . Пример — качели ( маятник ) с изменяемой длиной.

Негармонические колебания

Как установил в 1822 году Фурье , любое периодическое колебание может быть представлено как сумма гармонических колебаний путём разложения соответствующей функции в ряд Фурье . Среди слагаемых этой суммы существует гармоническое колебание с наименьшей частотой, которая называется основной частотой, а само это колебание — первой гармоникой или основным тоном, частоты же всех остальных слагаемых, гармонических колебаний, кратны основной частоте, и эти колебания называются высшими гармониками или обертонами — первым, вторым и т. д.

См. также

• Гармонический осциллятор
• Волна
• Резонанс
• Солитон
• Псевдогармонические колебания
• Операционное исчисление
• Дифференциальное уравнение
• Нелинейная система

Примечания

Литература

• Заболотнов Ю. М. от 8 марта 2016 на Wayback Machine
• А. А. Андронов , А. А. Витт , С. Э. Хайкин . . — М. : Государственное издательство физико-математической литературы, 1959. — 916 с. — 20 000 экз.
• Боголюбов Н. Н. Асимптотические методы в теории нелинейных колебаний. — М. : Государственное издательство физико-математической литературы, 1958. — 408 с.
• Н. В. Бутенин, Ю. И. Неймарк, Н. Л. Фуфаев. Теория нелинейных колебаний. — М. : Государственное издательство физико-математической литературы, 1976. — 385 с.

• Гукенхеймер Дж., Холмс Ф. Нелинейные колебания, динамические системы и бифуркации векторных полей. — М. : Государственное издательство физико-математической литературы, 2002. — 560 с. — ISBN 5-93972-200-8 .

• Кузнецов А. П. Нелинейные колебания: Учеб. пособие для вузов. — М. , 2002. — 292 с. — ISBN 5-94052-058-8 .

• Рабинович М. И., Трубецков Д. И. Теория колебаний и волн. — М. : «Регулярная и хаотическая динамика», 2000. — 560 с. — ISBN 5-93972-012-9 .
• Пять лекций по теории колебаний и волн : Учеб. пособие / Н.В. Карлов , Н.А. Кириченко ; М. ; Долгопрудный : МФТИ. - 157 с. : ил.; 27 см.; ISBN 5-7417-0011-X
• Н. В. Кузнецов. // Известия РАН. Теория и Системы управления. — 2020. — № 5 . — С. 5—27 . — doi : .