Interested Article - Задача о мятом рубле

Задача о мятом рубле , или задача о салфетке Маргулиса , — задача о математике оригами , первая задача в списке задач Арнольда .

Формулировка

Можно ли сложить прямоугольный лист бумаги в плоскую фигуру с периметром больше, чем у исходного прямоугольника? Рвать и резать бумагу, разумеется, нельзя.

В математически точной формулировке требуется уточнить, что значит «сложить». В зависимости от этого уточнения, ответом может быть «да», «нет» или «неизвестно».

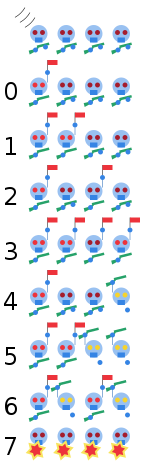
Например, если считать, что после каждого складывания лист бумаги склеивается с собой, то несложно доказать, что при каждом складывании периметр уменьшается, в частности, его нельзя увеличить. Однако, если рассмотреть сгибание и отгибание листа, как показано на рисунке, то легко видно, что при отгибании периметр увеличивается, хотя и остаётся меньше периметра исходного квадрата. Неизвестно, можно ли увеличить периметр, пользуясь только сгибаниями и отгибаниями.

Тем не менее, если разрешить одновременно сгибать лист вдоль нескольких складок, то увеличить периметр, оказывается, можно . Подобные сложные складки распространены в оригами , и именно оригамисты первыми сумели продвинуться в решении задачи. С одной стороны, в оригами часто растягивают или сжимают бумагу, что недопустимо в математической формулировке. С другой стороны, идеальная математическая «бумага» не имеет толщины, и даже большие «сэндвичи» можно свободно складывать .

История

Этот вопрос часто называют фольклорным, но, по-видимому, он был впервые сформулирован Арнольдом в 1956 году . На Западе задача стала известна под названием «задача о салфетке Маргулиса ».

Основной шаг в частичном решении задачи был сделан оригамистами . Частичные решения были предложены , Лэнгом , Ященко . Наиболее полное решение было представлено .

Примечания

↑ Антон Айзенберг. от 30 июня 2016 на Wayback Machine , Научно-популярные задачи на «Элементах»: Математика.
В. И. Арнольд . Задача 1956-1 // . — Фазис, 2000. — С. . — 454 с. — ISBN 5-7036-0060-X .
от 26 октября 2009 на Wayback Machine . от 6 января 2010 на Wayback Machine .
S. Krat, Approximation Problems in Length Geometry, Ph.D. thesis, Pennsylvania State University, 2005
R. Lang, Origami Design Secrets; AK Peters, Ltd., 2003
I. Yaschenko. (неопр.) // Math. Intelligencer. — 1998. — Т. 20 , № 2 . — С. 36—40 . — doi : .
А. Тарасов. // Чебышевский сборник. — 2004. — Т. 5 , вып. 1 . — С. 174—187 . 20 августа 2014 года.

Ссылки

Антон Айзенберг. (рус.) // Элементы.ру . — 2014. — 3 марта.
В. И. Арнольд. . — М. : МЦНМО , 2004. — 16 с. — ISBN 5-94057-183-2 .
А. Петрунин. // Задачи Санкт-петербургской олимпиады школьников по математике. — 2008.
/ Математические этюды
/ Математические этюды