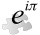Суммы Вейля — общее название тригонометрических сумм специального вида.

Определение

Суммами Вейля называются суммы вида

${\displaystyle \displaystyle \sum _{a<n\leqslant b}e^{2\pi if(n)}}$ ,

где ${\displaystyle n\in \mathbb {Z} }$ , а функция

${\displaystyle f(x)=\alpha _{k}x^{k}+\alpha _{k-1}x^{k-1}+\ldots +\alpha _{1}x+\alpha _{0}\in \mathbb {R} [x]}$

есть многочлен степени ${\displaystyle k}$ с вещественными коэффициентами. Название "суммы Вейля" для тригонометрических сумм такого вида было предложено И.М. Виноградовым в честь впервые подробно рассмотревших их Г. Вейля .

Рациональные суммы Вейля

Важным примером сумм Вейля являются рациональные суммы Вейля, когда все коэффициенты многочлена ${\displaystyle f(x)}$ — рациональные числа. Более точно, рациональными суммами Вейля (по модулю ${\displaystyle m}$ ) называются суммы Вейля с функцией ${\displaystyle f(x)={\frac {P_{k}(x)}{m}}}$ :

${\displaystyle \displaystyle \sum _{a<n\leqslant b}e^{2\pi i{\frac {P_{k}(n)}{m}}}}$ ,

где ${\displaystyle m>1}$ — некоторое фиксированное целое число, ${\displaystyle n\in \mathbb {Z} }$ , а

${\displaystyle P_{k}(x)=a_{k}x^{k}+a_{k-1}x^{k-1}+\ldots +a_{1}x+a_{0}\in \mathbb {Z} [x]}$

есть многочлен степени ${\displaystyle k}$ с целыми коэффициентами.

Примеры рациональных сумм Вейля

• Если ${\displaystyle f(x)=ax}$ , то указанная сумма является линейной тригонометрической суммой .
• Если ${\displaystyle m=p}$ — простое число, то суммы Вейля с многочленом ${\displaystyle f(x)=ax^{k}}$ ${\displaystyle (k>1)}$ называются суммами Гаусса порядка ${\displaystyle k}$ , а при ${\displaystyle k=2}$ — суммами Гаусса .
• Если ${\displaystyle m=p}$ — простое число, то для каждого ${\displaystyle n}$ , не кратного ${\displaystyle p}$ , в поле вычетов ${\displaystyle \mathbb {Z} _{p}}$ всегда существует число ${\displaystyle n^{*}}$ , обратное к ${\displaystyle n}$ :

${\displaystyle n^{*}n\equiv 1\mod p}$ , и при этом ${\displaystyle n^{*}\equiv n^{p-2}\mod p}$ .

Таким образом, рациональные суммы Вейля с многочленом ${\displaystyle P_{p-1}(n)=an^{p-1}+bn}$ могут быть записаны в виде

${\displaystyle \displaystyle {\sum _{a<n\leqslant b}}'e^{2\pi i{\frac {an^{*}+bn}{p}}}}$ ,

(штрих у знака суммы означает, что суммирование ведется по всем ${\displaystyle n}$ , не кратным ${\displaystyle p}$ ) и называются суммами Клостермана .

Оценки сумм Вейля

Оценки сумм Вейля играют важную роль в многих задачах аналитической теории чисел . Существует несколько методов оценки сумм Вейля. Наиболее простой и известный из них — метод Гаусса.

См. также

• Теорема Вейля о равномерном распределении

Литература

• Г.И. Архипов, А.А. Карацуба, В.Н. Чубариков. Теория кратных тригонометрических сумм. М.: Наука, 1987.
• И.М. Виноградов. Избранные труды. М., 1952.