Interested Article - Поверхностные акустические волны в пьезоэлектриках

- 2020-01-25
- 2

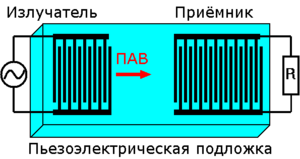
Поверхностные акустические волны в пьезоэлектриках — упругие волны распространяющиеся около поверхности пьезоэлектрика ( релеевские волны ) или в тонких пьезоэлектрических плёнках (лэмбовские волны наблюдаются, когда толщина подложки сравнима с длиной волны), сопровождающиеся модуляцией электрического поля для пьезоэлектрически активных направлений. Движение частиц среды при обоих типах волн эллиптическое. Амплитуда релеевских волн спадает при удалении от поверхности и её можно рассматривать как затухающую волну. Метод генерации ПАВ в пьезоэлектриках с помощью встречно-гребёнчатого преобразователя предложен в 1965 году , что позволило найти широкое применение в обработке высокочастотных сигналов, линиях задержки, сенсорах и, в последнее время, для манипулирования частицами в микроканалах.
Теоретические основания
В линейной среде акустические волны полностью характеризуются уравнениями для смещений частиц U i и потенциалом φ :
| (1.1) |
| (1.2) |
| (1.3) |
| (1.4) |
| (1.5) |
где T ij , S ij — тензоры напряжений и деформаций; E , D — векторы напряженности и индукции электрического поля; C ijkl , e ijk , ε ij — тензоры модулей упругости (этот тензор симметричен по последней паре индексов ), пьезомодулей и диэлектрической проницаемости соответственно; ρ — плотность среды. По повторяющимся индексам производится суммирование. Тензор модулей упругости задан при постоянном электрическом поле, а тензор диэлектрической проницаемости при постоянной деформации. Если пьезоэлектрик не содержит свободных зарядов, то его можно считать диэлектриком и для него выполняется закон Гаусса для индукции электрического поля:
| (2) |
Собственные полупроводники при достаточно низкой температуре удовлетворяют этому условию. Из вышеприведённой системы уравнений можно получить уравнения для акустических волн в пьезоэлектрике
| (3.1) |
| (3.2) |
Данные уравнения с граничными условиями полностью определяют задачу. При отсутствии пьезоэффекта решения уравнения ( ) представляют собой упругие волны в анизотропной линейной среде.
Парциальные волны
Ищем решение уравнений ( ) и ( ) в виде плоских волн распространяющихся в направлении x 1 и затухающие в направлении x 3 :
| (4.1) |
| (4.2) |
Подставляя эти решения в волновые уравнения получим систему уравнений на амплитуды
| (5.1) |
где элементы выражаются как
| (5.2) |
Чтобы нетривиальное решение уравнений существовало, нужно чтобы детерминант системы ( ) был равен нулю. Это условие задаёт уравнение 8-й степени относительно b. Выбирая только решения в нижней комплексной мы найдём полное решение волновых уравнений:
| (6.1) |
| (6.2) |
где неизвестные коэффициенты C m находятся из граничных условий заданных на поверхности пьезоэлектрика: условия ненагруженной поверхности T 33 =T 31 =T 32 =0 и непрерывности нормальной компоненты вектора электрической индукции D 3 . Для граничных условий (показан m-ый столбец) получим систему уравнений:
| (7) |
Из равенства детерминанта системы нулю находят фазовую скорость волны .
Симметрия кристаллов
Используя нотацию Фойгта тензор модулей упругости можно переписать в виде симметричной матрицы 6×6, которая имеет в общем случае 21 линейно независимую компоненту . Для кристаллов кубической симметрии ( кремний , арсенид галлия ), где координатная система совпадает с осями кристаллической решётки есть только три независимые компоненты :
Для кристаллов гексогональной симметрии ( сульфид кадмия , окись цинка ), где ось x 3 совпадает с осью Z кристалла существует пять независимых компонент :
Для кристаллов тригональной симметрии (классы 32, 3 m , ), выделяют шесть независимых компонент :
К этому классу относятся важные пьезоэлектрики такие как кварц , ниобат лития .
Тензор пьезоэлектрических постоянных в нотации Фойгта (последняя пара индексов заменяется) для кубической сингонии (классы 23 и ) имеют одну независимую компоненту
Для кристаллов с гексогональной симметрией (точечная группа 6 mm , поляризованная керамика по оси x 3 ) — три компоненты:
Для точечной группы 32 ( тригональная сингония ) две компоненты:
а для точечной группы 3 m — четыре :
Тензор диэлектрических постоянных также зависит от направления в кристалле для групп 3 m , 32, 6 mm , и ε 33 ≠ε 11 =ε 22 . Для классов 23, , m 3 m : ε 33 =ε 11 =ε 22 .
Взаимодействие ПАВ в пьезоэлектрике с ДЭГ
Рассмотрим простейший одномерный случай и, отбрасывая индексы, перепишем систему уравнений ( ) в виде :
| (8.1) |
| (8.2) |
| (8.3) |
| (8.4) |
Эта систему уравнений приводит к волновому уравнению для сдвига
| (9) |
В случае если пьезоэлектрик окажется хорошим проводником, то продольные звуковые волны (скорость ) не будут пьезоэлектрическими, а если — диэлектриком, то скорость волны станет . Коэффициент называется коэффициент электромеханической связи и принимает значения меньше 0,05 (для поверхности (100) GaAs в направлении [011] K² eff =6.4×10 −4 ). Если в GaAs сформирован ДЭГ с проводимостью σ, то электрическое поле акустической волны приводит к потерям энергии из-за омических потерь. Коэффициент затухания Γ и изменение скорости пьезоакустической волны с частотой ω равны соответственно:
| (10.1) |
| (10.2) |
где λ — длина волны, σ M =v 0 (1+ε). Здесь расстояние до ДЭГ от поверхности много меньше длины волны. В более общем случае изменение скорости и затухание связаны соотношением :
| (11) |
где v s — скорость акустической волны для идеального проводника, q — волновой вектор, а коэффициенты α и σ M зависят от материальных параметров. Отсюда видно, что взаимодействие ПАВ с ДЭГ зависит от продольной компоненты терзора проводимости, определяя бесконтактный метод его измерения.
Из-за наличия затухания часть импульса волны передаётся ДЭГ, приводя к возникновению акустоэлектрического тока (если цепь замкнута). Связь затухания и фазового сдвига с проводимостью благодаря взаимодействию ПАВ в пьезоэлектрике с ДЭГ изучалась в присутствии перпердикулярного магнитного поля в режиме целочисленного квантового эффекта Холла и дробного квантового эффекта Холла
Усиление ПАВ в полупроводниках с пьезоэлектрическими свойствами
Система уравнений для одномерного случая ( ) в полупроводниках n-типа с пьезоэлектрическими свойствами следует дополнить уравнениями для полного тока (включает дрейфовую и диффузионную части)
| (12) |
уравнением непрерывности
| (13) |
и теоремой Гаусса
| (14) |
Здесь μ — подвижность, q — элементарный заряд, D n — коэффициент диффузии, концентрация электронов n c состоит из постоянной части n 0 и меняющейся во времени вклада n s из-за действия электрического поля акустической волны. Помимо переменного электрического поля E 1 e jkx-jωt действует постоянное поле E 0 .
Коэффициент затухания в этом случае равен
| (15) |
где , , . Если дрейфовая скорость v d электронов больше скорости волны то γ меняет знак и, соответственно, вместо затухания происходит усиление поверхностной акустической волны.
Адиабатический транспорт в одномерных каналах
Взаимодействие ПАВ в пьезоэлектрике с ДЭГ можно распространить на одномерные каналы, а именно сформированные с помощью латеральных затворов на поверхности GaAs. Бегущая ПАВ благодаря электрическому полю может создавать движущуюся потенциальную яму для отдельного электрона (которую можно представить как квантовую точку ) в перекрытом одномерном канале, то есть индуцировать проводимость. Благодаря кулоновской блокаде за один период переносится один электрон, и результирующий ток определяется только частотой сигнала f и зарядом электрона :
Такая простая формула открывает возможность использовать транспорт в квази-одномерных каналах в качестве эталона силы тока.
Применение
Датчики на поверхностных акустических волнах , линии задержки .
Примечания
- White R. M., Voltmer F. W. // Appl. Phys. Lett.. — 1965. — Т. 7 . — С. 314—316 . — doi : . (недоступная ссылка)
- Осетров А. В., Шо Н. В. // Вычислительная механика сплошных сред. — 2011. — Т. 4 . — С. 71—80 . 4 марта 2016 года.
- , с. 131.
- , с. 18—21.
- , с. 11.
- ↑ , с. 12.
- ↑ , с. 14.
- ↑ Wixforth A., Scriba J., Wassermeier M., Kotthaus J. P., Weimann G., Schlapp W. // Phys. Rev. B. — 1989. — Т. 40 . — С. 7874—7887 . — doi : .
- Simon S. H. // Phys. Rev. B. — 1996. — Т. 54 . — С. 13878—13884 . — doi : .
- Willett R. L., Paalanen M. A., Ruel R. R., West K. W., Pfeiffer L. N., Bishop D. J. // Phys. Rev. Lett.. — 1990. — Т. 65 . — С. 112—115 . — doi : .
- White D. L. // J. Appl. Phys.. — 1962. — Т. 33 . — С. 2547—2554 . — doi : . (недоступная ссылка)
- Shilton J. M., Talyanskii V. I., Pepper M., Ritchie D. A., Frost J. E. F., Ford C. J. B., Smith C. G., Jones G. A. C. // J. Phys.: Condens. Matter. — 1996. — Т. 8 . — С. 531 . — doi : .
- Thouless D. J. // Phys. Rev. B. — 1983. — Т. 27 . — С. 6083—6087 . — doi : .
Литература
- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. — М. : Наука, 1987. — Т. VII. Теория упругости. — 248 с.
- Фильтры на поверхностных акустических волнах (расчёт, технология и применение) = Surface wave filters: design, constructin, and use / Под ред. В. Б. Акпамбетова. — М. : Радио и связь, 1981. — 472 с. — 5000 экз.
- Морган Д. Устройства обработки сигналов на поверхностных акустических волнах = Surface-Wave Devices for Signal Processing / Под ред. С. И. Баскакова. — М. : Радио и связь, 1990. — 414 с. — ISBN 5256006614 .
- 2020-01-25
- 2








![{\displaystyle u_{j}^{m}=\alpha _{j}^{m}\mathrm {exp} (ikb^{m}x_{3})\mathrm {exp} [ik(x_{1}-vt)],}](/images/007/580/7580326/10.jpg?rand=563286)
![{\displaystyle \phi ^{m}=\alpha _{4}^{m}\mathrm {exp} (ikb^{m}x_{3})\mathrm {exp} [ik(x_{1}-vt)],}](/images/007/580/7580326/11.jpg?rand=275048)


![{\displaystyle u_{j}=\left[\sum _{m}C_{m}\alpha _{j}^{m}\mathrm {exp} (ikb^{m}x_{3})\right]\mathrm {exp} [ik(x_{1}-vt)],}](/images/007/580/7580326/14.jpg?rand=594523)
![{\displaystyle \phi =\left[\sum _{m}C_{m}\alpha _{4}^{m}\mathrm {exp} (ikb^{m}x_{3})\right]\mathrm {exp} [ik(x_{1}-vt)],}](/images/007/580/7580326/15.jpg?rand=83345)


























![{\displaystyle \Gamma ={\frac {K^{2}}{2}}{\frac {\omega _{c}}{v_{0}\gamma }}\left[1+{\frac {\omega _{c}^{2}}{\gamma ^{2}\omega ^{2}}}\left(1+{\frac {\omega ^{2}}{\omega _{c}\omega _{D}}}\right)^{2}\right]^{-1}}](/images/007/580/7580326/42.jpg?rand=479386)