Interested Article - Автокорреляционная функция

График 100 случайных величин, суммированный с синусоидальным сигналом малой амплитуды . График автокорреляционной функции позволяет увидеть периодичность в ряде данных.

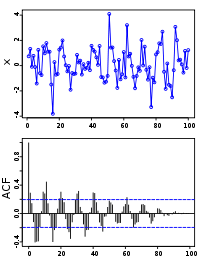
Автокорреляционная функция (АКФ) — зависимость взаимосвязи между функцией (сигналом) и её сдвинутой по аргументу функции копией от величины сдвига.

Для детерминированных сигналов автокорреляционная функция ( АКФ ) сигнала $f(t)$ $f(t)$ определяется интегралом :

\Psi (\tau)=\int _{-\infty }^{\infty }f(t)f^{*}(t-\tau)\mathrm {d} t,

\Psi (\tau)=\int _{-\infty }^{\infty }f(t)f^{*}(t-\tau)\mathrm {d} t,

и показывает связь сигнала (функции $\;f(t)$ $\;f(t)$ ) с копией самого себя, смещённого на величину $\tau$ $\tau$ . Звёздочка означает комплексное сопряжение .

Для случайных процессов АКФ случайной функции $X(t)$ $X(t)$ имеет вид :

K(t,\tau)=\mathbb {E} \{X(t)X^{*}(t-\tau)\}

K(t,\tau)=\mathbb {E} \{X(t)X^{*}(t-\tau)\}

,

где

\mathbb {E} \{\ \}

\mathbb {E} \{\ \}

— математическое ожидание , звёздочка означает комплексное сопряжение .

Если исходная функция строго периодическая , то на графике автокорреляционной функции тоже будет строго периодическая функция. Таким образом, из этого графика можно судить о периодичности исходной функции, а, следовательно, и о её частотных характеристиках. Автокорреляционная функция применяется для анализа сложных колебаний , например, электроэнцефалограммы человека.

Применение в технике

Корреляционные свойства кодовых последовательностей, используемых в широкополосных системах, зависят от типа кодовой последовательности, её длины, частоты следования её символов и от её посимвольной структуры.

Изучение АКФ играет важную роль при выборе кодовых последовательностей с точки зрения наименьшей вероятности установления ложной синхронизации.

Другие применения

Автокорреляционная функция играет важную роль в математическом моделировании и анализе временных рядов , показывая характерные времена для исследуемых процессов (см., например: Турчин П. В. Историческая динамика. М.: УРСС , 2007. ISBN 978-5-382-00104-3 ). В частности, циклам в поведении динамических систем соответствуют максимумы автокорреляционной функции некоторого характерного параметра.

Скоростное вычисление

Часто приходится вычислять автокорреляционную функцию для временного ряда $x_{i}$ $x_{i}$ . Вычисление «в лоб» работает за $O(T^{2})$ $O(T^2)$ . Однако есть способ сделать это за $O(T\log T)$ $O(T \log T)$ .

Метод основан на теореме Хинчина — Колмогорова (она же Винера — Хинчина), утверждающей, что автокорреляционная функция сигнала есть фурье-образ его спектральной плотности мощности . Поскольку для дискретных сигналов для вычисления их спектров существует алгоритм быстрого преобразования Фурье , имеющий порядок сложности $O(T\log T)$ $O(T \log T)$ , то имеется возможность ускорить вычисление автокорреляционной функции за счет вычисления спектра сигнала, затем его мощности (квадрата модуля) и затем обратного фурье-преобразования.

Суть способа состоит в следующем. Можно сделать некое обратное взаимно однозначное преобразование данных, называемое преобразованием Фурье , которое поставит им во взаимно однозначное соответствие набор данных в другом пространстве, называемом пространством частот (частотный спектр сигнала — набор спектральных амплитуд). Вместо прямого вычисления автокорреляционной функции на наших исходных данных можно произвести соответствующую ей операцию над соответствующими данными в пространстве частот Фурье-спектра, что делается за линейное время O(T) — вычислению автокорреляционной функции в пространстве частот соответствует вычисление мощностей частот возведением в квадрат модулей спектральных амплитуд. После этого мы по полученным спектральным мощностям восстановим соответствующие им в обычном пространстве значения автокорреляционной функции. Вычисление спектра по функции и обратно делается с помощью быстрого преобразования Фурье за $O(T\log T)$ $O(T \log T)$ , вычисление спектральной плотности мощности в пространстве частот — за O(T). Таким образом, мы получили выигрыш по времени при вычислениях.

Подготовка. Вычитаем из ряда среднее арифметическое . Преобразуем в комплексные числа . Дополняем нулями до $2^{k}$ $2^k$ . Затем дописываем в конец ещё $2^{k}$ $2^k$ нулей.

Вычисление. Автокорреляционная функция вычисляется с помощью быстрого преобразования Фурье и прямо пропорциональна первым $n$ $n$ элементам последовательности: