Статья «Эллипс» входит в общий для всех языковых разделов Википедии расширенный список необходимых статей . Её развитие вплоть до статуса избранной является важным направлением работы русского раздела Википедии. Вы можете посетить страницу проекта «Мириада» , который занимается улучшением наиболее важных статей Википедии , и, при желании, присоединиться к нему.

Проект «Математика» Эта статья тематически связана с вики-проектом «Математика» , цель которого — создание и улучшение статей по темам, связанным с математикой . Вы можете , а также присоединиться к проекту , принять участие в его обсуждении и поработать над требуемыми статьями . ??? Статью ещё никто не оценил по шкале оценок проекта

Енот что ли?

Таково название этой формулы. Дано оно её создателями или нет — не знаю.-- NightSky ^{[ источник? ]} 14:16, 10 ноября 2008 (UTC) [ ]

Присоединяюсь. Из статьи не понятно, что это за 4 буквы перед формулой. Андрей П 18:13, 13 марта 2010 (UTC) [ ]

Кто раскроет подробнее, будет прекрасно, а то какие-то 0.3619 % ^{[ источник? ]} . Андрей П 18:13, 13 марта 2010 (UTC) [ ]

Мне кажется, что c = | F1F2 |/2 (забыли поделить на двоечку).

Убрал построение по дву причинам:

1. по-сути «построения» являются пережёвыванием определения

2. эллипс не строится --- строятся только какие-то точки на нём.-- Тоша 22:00, 24 июля 2009 (UTC) [ ]

Вернул раздел — давайте искать консенсус...

1. Не согласен, т.к. начертить циркулем эллипс — задача нетривиальная. Вывести алгоритм построения из определения самостоятельно достаточно сложно, поэтому эта информация и даётся в математических справочниках (Конкретно эта информация взята из справочника Корнов, наверное, знаете такой? Вечером добавлю ссылку на конкретную страницу). Поэтому я считаю, что и Википедия должна содержать материалы такого рода.

2. Да, эти два алгоритма строят точки эллипса и соединив их отрезками прямых, получится ломаная, а не истинный эллипс. Но не надо доводить до абсурда — увеличивая число точек можно добиться желаемой точности. Ровно также и реальные материалы (бумага), инструменты (карандаш, циркуль) и техника (монитор, принтер) устанавливают предел точности.

Вот как-то так. -- Sergey kudryavtsev 08:28, 2 апреля 2010 (UTC) [ ]

Построение с помощью двух иголок и нитки

Поскольку сумма расстояний от каждого фокуса до любой точки эллипса постоянна, то в быту эллипс (например в садоводстве) строится так: в каждый из фокусов забивается по колу, к которым свободно привязывается шнур, длина которого определяет малую ось. Затем третьим колом ведут линию по земле, постоянно прижимая его к шнуру. Если работать аккуратно, то получается вполне недурно. Витольд Муратов ( обс , вклад ) 20:46, 31 мая 2010 (UTC) [ ]

Удобнее не привязывать шнур к колам, а связать шнур в кольцо и надеть его на оба фиксированных кола — тогда не будет проблемы перехвата в концах большой оси эллипса. — Monedula 08:37, 1 июня 2010 (UTC) [ ]

Я так строил эллипсы на начертательной геометрии на чертежах — написал подглаву «С помощью двух иголок и нитки». Способ этот я вычитал в какой-то научно-популярной книге по математике или по физике (возможно у Мартина Гарднера ). На чертежах получалось хорошо. Правда, связывать нить в кольцо я не додумался (вернее, не я не додумался, а источник не сообщил, или я в источнике не увидел) — надо бы дополнить подглаву этой идеей. -- Кеель 2011.май.25.ср. 12:33 (московское время) -- Кеель 08:36, 25 мая 2011 (UTC) [ ]

А зачем в садоводстве чертить на земле эллипс? -- Кеель 2011.май.25.ср. 12:34 (московское время) -- Кеель 08:36, 25 мая 2011 (UTC) [ ]

Дополню: Чтобы нить не сваливалась с грифеля карандаша вниз, на лист бумаги можно положить шайбу от резьбового соединения (желательно взять шайбу потолще, но не слишком), и оттягивающим нить грифелем карандаша касаемся бумаги внутри отверстия шайбы — чтобы оттянутая нить во время рисования эллипса лежала на шайбе. -- Кеель 2011.июнь.10.пт. 06:35 (московское время) -- Кеель 02:37, 10 июня 2011 (UTC) [ ]

В параметрической формуле эллипса ${\displaystyle {\begin{cases}x=a\,\cos t\\y=b\,\sin t\end{cases}}\;\;\;0\leqslant t\leqslant 2\pi }$ , параметр t не является углом между радиус вестором точки и осью X.

Это становится очевидным, если мы запишем проекции радиус вектора точки на эллипсе с параметрами ${\displaystyle (r,\phi )}$ на оси X и Y:

${\displaystyle X=r(\phi )\,\ cos(\phi )}$ ,

${\displaystyle Y=r(\phi )\,\ sin(\phi )}$

Очевидно, что ${\displaystyle r(\phi )}$ - переменная величина, зависящая от угла. В параметрической формуле же, перед синусом и косинусом стоят константы.

Поэтому и формула для радиуса эллипса полученная из параметрического уравнения ( ${\displaystyle ~R^{2}=a^{2}\cos ^{2}t+b^{2}\sin ^{2}t,}$ ) так же не верна.

Правильная формула выводится при помощи канонического уравнения эллипса. Её так же можно посмотреть в английской версии статьи про эллипс.

Tetsuzin 05:57, 13 февраля 2012 (UTC) [ ]

Нигде и не утверждается, что параметр t является углом между радиус-вектором точки и осью X. Разве параметр обязан быть этим углом? — Monedula 16:55, 8 августа 2013 (UTC) [ ]

Да, верно, но основная претензия была к формуле радиуса эллипса, в которой полагалось что t это угол. Tetsuzin 11:42, 12 ноября 2013 (UTC) [ ]

«Кривую на плоскости можно рассматривать как траекторию движущейся точки и описывать, задавая координаты точки на плоскости как функции какой-то переменной. Мы приходим к системе двух уравнений

                              x=φ(t).      x=β(t)

Такие системы называются параметрическими уравнениями кривой, а переменная t- параметром. Его содержательный смысл не является существенным, да и происхождение параметра может быть различным – не только исходя из механической интерпретации кривой как траектории движения» (Извлечение из курса аналитической геометрии)

 Я привожу это определение параметрической системы уравнений кривой на плоскости как полагание, на которое можно опереться при осмыслении содержательного смысла параметра.  Математическое выражение - матаппарат, как и богиня правосудия Фемида, слепо отражает реальность. Одно математическое выражение может отражать как процесс теплопроводности так например и вязкости, а параметром может быть температура, давление, высота, глубина, проводимость, угол - что угодно. Откуда и вытекает, что содержательный смысл параметра t не является существенным именно в этих смыслах. Но это надо осознаватьBerdi Ovezov (обс.) 17:33, 10 августа 2023 (UTC)Berdi Ovezov (обс.) 10:20, 8 августа 2023 (UTC)[]

С чего это соотношение a^2=b^2+c^2 было помечено 23 февраля как неверное? Да ещё и так криво... Ну, понятно, праздник и всё такое, но зачем так мудрить?

Специально для автора упомянутой правки: данное выражение является другой формой записи фундаментального определения эллипса как "геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F_1 и F_2 (называемых фокусами) постоянна и больше расстояния между фокусами".

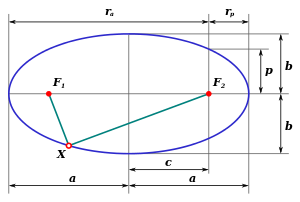
Будем перемещать точку X на иллюстрации "Части эллипса" в разделе "Соотношения между элементами эллипса" против часовой стрелки до точки пересечения эллипса и малой полуоси (на 6 часах). Длина ломаной F_1 X F_2 постоянна (по определению) и равна 2*a (для доказательства последнего утверждения достаточно рассмотреть случай, когда точка X находится на 9 часах), значит, в рассматриваемой точке длина отрезка XF_1 равна a (равнобедренный треугольник). Центр эллипса обозначим символом O. В прямоугольном треугольнике OXF_1 катет OF_1 равен по определению c, а катет OX - малой полуоси b. Квадрат гипотенузы как бы примерно соответствует сумме квадратов катетов, не? Михаил Каганский 13:02, 24 февраля 2014 (UTC) [ ]

Интересное обсуждение этой темы на сайте . Однако, в статье указывается дата 16 декабря 2011 года, а не двадцать шестого дня. 2A00:1370:8128:73E:D9FD:99C6:3B41:7EE5 18:40, 14 июля 2016 (UTC) [ ]

• Я уже не первый день размышляю на тему точной формулы для периметра эллипса. Первое моё полагание - формула не должна содержать элементы интегрирования и дифференцирования. То есть она не должна выходить за рамки основных постулатов Евклидовой геометрии. Можно ли в принципе надеяться, что в рамках Евклидовой геометрии существует возможность нахождения геометрической функции, выражающей периметр эллипса? Или кто то уже знает запрет на существование такой функции, такой например, как запрет на одновременное определение координаты и скорости частицы микромира? Это я о принципе неопределённости Гейзенберга. Существует ли такой "принцип неопределённости периметра эллипса". Если нет - то ещё не всё потеряно. Если у кого-то есть по этому поводу какие либо мысли, прошу поделиться. Berdi Ovezov ( обс. ) 19:53, 22 сентября 2023 (UTC) [ ]

"его фокальное расстояние" Откуда перед знаком корня двойка? Berdi Ovezov ( обс. ) 01:54, 26 сентября 2023 (UTC) [ ]

• Это не фокальное расстояние, это расстояние между фокусами. Там и обозначение F1;F2. А если фокальное расстояние - то двойку перед корнем долой! Berdi Ovezov ( обс. ) 09:55, 26 сентября 2023 (UTC) [ ]