Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений , нахождения обратной матрицы , нахождения координат вектора в заданном базисе или отыскания ранга матрицы . Метод является модификацией метода Гаусса . Назван в честь К. Ф. Гаусса и немецкого геодезиста и математика Вильгельма Йордана .

Алгоритм

1. Выбирают первый слева столбец матрицы , в котором есть хоть одно отличное от нуля значение.
2. Если самое верхнее число в этом столбце ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.
3. Все элементы первой строки делят на верхний элемент выбранного столбца.
4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.
5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.
6. После повторения этой процедуры ${\displaystyle n-1}$ раз получают верхнюю треугольную матрицу
7. Вычитают из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали .
8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

Расширенный алгоритм для нахождения обратной матрицы

Пусть дано :

${\displaystyle A={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &a_{nn}\end{pmatrix}}\quad a_{11}\neq 0\quad I={\begin{pmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{pmatrix}}}$

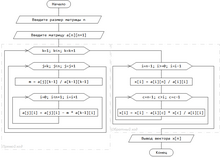
Прямой ход (алгоритм образования нулей под главной диагональю)

• Разделим первую строку матрицы А на ${\displaystyle a_{11}}$ получим: ${\displaystyle a_{1j}^{1}={\frac {a_{1j}}{a_{11}}}}$ , j — столбец матрицы А.
• Повторяем действия для матрицы I, по формуле: ${\displaystyle b_{1s}^{1}={\frac {b_{1s}}{a_{11}}}}$ , s — столбец матрицы I

Получим:

${\displaystyle A={\begin{pmatrix}1&a_{12}^{1}&\cdots &a_{1n}^{1}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &a_{nn}\end{pmatrix}}\qquad I={\begin{pmatrix}b_{11}^{1}&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{pmatrix}}}$

• Будем образовывать 0 в первом столбце : ${\displaystyle a_{2j}^{1}=a_{2j}-a_{1j}^{1}a_{21}\ ,\dots ,\ a_{nj}^{1}=a_{nj}-a_{1j}^{1}a_{n1}}$
• Повторяем действия для матрицы І, по формулам : ${\displaystyle b_{2s}^{1}=b_{2s}-b_{1s}^{1}a_{21}\ ,\dots ,\ b_{ns}^{1}=b_{ns}-b_{1s}^{1}a_{n1}}$

Получим:

${\displaystyle A={\begin{pmatrix}1&a_{12}^{1}&\cdots &a_{1n}^{1}\\0&a_{22}^{1}&\cdots &a_{2n}^{1}\\\vdots &\vdots &\ddots &\vdots \\0&a_{n2}^{1}&\cdots &a_{nn}^{1}\end{pmatrix}}\qquad I={\begin{pmatrix}b_{11}^{1}&0&\cdots &0\\b_{21}^{1}&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\b_{n1}^{1}&0&\cdots &1\end{pmatrix}}}$

• продолжаем выполнять аналогичные операции, используя формулы : ${\displaystyle a_{ij}^{k}={\frac {a_{ij}^{k}}{a_{ii}}}\qquad a_{ij}^{k}=a_{ij}^{k-1}-a_{kj}^{k}a_{ik}^{k-1}}$

при условии, что ${\displaystyle k=1\rightarrow n,i=k+1\rightarrow n,j=1\rightarrow n}$

• Повторяем действия для матрицы І, по формулам : ${\displaystyle b_{ik}^{k}={\frac {b_{ik}^{k}}{a_{ii}}}\qquad b_{is}^{k}=b_{is}^{k-1}-b_{ks}^{k}a_{ik}^{k-1}}$

при условии, что ${\displaystyle k=1\to n,\;i=k+1\to n,\;s=1\to n}$

Получим :

${\displaystyle A={\begin{pmatrix}1&a_{12}^{1}&\cdots &a_{1n}^{1}\\0&1&\cdots &a_{2n}^{2}\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{pmatrix}}\qquad I={\begin{pmatrix}b_{11}^{1}&0&\cdots &0\\b_{21}^{2}&b_{22}^{2}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\b_{n1}^{n}&b_{n2}^{n}&\cdots &b_{nn}^{n}\end{pmatrix}}}$

Обратный ход (алгоритм образования нулей над главной диагональю)

Используем формулу: ${\displaystyle a_{ij}^{k-1}=a_{ij}^{k-1}-a_{ij}^{k}a_{ik}^{i}}$ , при условии, что ${\displaystyle k=n\to 1,\;i=1\to k-1,\;j=1\to n}$

Повторяем действия для матрицы І, по формуле : ${\displaystyle b_{is}^{k-1}=b_{is}^{k-1}-b_{is}^{k}a_{ik}^{i}}$ , при условии, что ${\displaystyle k=n\to 1,\;i=1\to k-1,\;s=1\to n}$

Окончательно получаем :

${\displaystyle A={\begin{pmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{pmatrix}}\qquad I=A^{-1}}$

Пример

Для решения следующей системы уравнений :

${\displaystyle \left\{{\begin{array}{ccccccl}a&+&b&+&c&=&0\\4a&+&2b&+&c&=&1\\9a&+&3b&+&c&=&3\end{array}}\right.}$

Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

${\displaystyle {\begin{pmatrix}1&1&1\!&\vline &\!0\\4&2&1\!&\vline &\!1\\9&3&1\!&\vline &\!3\end{pmatrix}}}$

Проведём следующие действия:

• К строке 2 добавим: −4 × Строку 1.
• К строке 3 добавим: −9 × Строку 1.

Получим:

${\displaystyle {\begin{pmatrix}1&\ 1&\ 1\!&\vline &\!0\\0&-2&-3\!&\vline &\!1\\0&-6&-8\!&\vline &\!3\end{pmatrix}}}$

• К строке 3 добавим: −3 × Строку 2.
• Строку 2 делим на −2

${\displaystyle {\begin{pmatrix}1&1&1\!&\vline &\!\ 0\\0&1&{3 \over 2}\!&\vline &\!-{1 \over 2}\\0&0&1\!&\vline &\!\ 0\end{pmatrix}}}$

• К строке 1 добавим: −1 × Строку 3.
• К строке 2 добавим: −3/2 × Строку 3.

${\displaystyle {\begin{pmatrix}1&1&0\!&\vline &\!\ 0\\0&1&0\!&\vline &\!-{1 \over 2}\\0&0&1\!&\vline &\!\ 0\end{pmatrix}}}$

• К строке 1 добавим: −1 × Строку 2.

${\displaystyle {\begin{pmatrix}1&0&0\!&\vline &\!\ {1 \over 2}\\0&1&0\!&\vline &\!-{1 \over 2}\\0&0&1\!&\vline &\!\ 0\end{pmatrix}}}$

В правом столбце получаем решение:

${\displaystyle a={\frac {1}{2}}\;;\ b=-{\frac {1}{2}}\;;\ c=0}$ .

Реализация алгоритма на языке программирования C#

namespace Gauss_Jordan_Method
{
    class Maths
    {
        /// <summary>
        /// Метод Гаусса-Жордана (Обратная матрица)
        /// </summary>
        /// <param name="Matrix">Начальная матрица</param>
        /// <returns></returns>
        public static double[,] GaussJordan(double[,] Matrix)
        {
            int n = Matrix.GetLength(0); //Размерность начальной матрицы

            double[,] xirtaM = new double[n, n]; //Единичная матрица (искомая обратная матрица)
            for (int i = 0; i < n; i++)
                xirtaM[i, i] = 1;

            double[,] Matrix_Big = new double[n, 2*n]; //Общая матрица, получаемая скреплением Начальной матрицы и единичной
            for (int i = 0; i < n; i++)
                for (int j = 0; j < n; j++)
                {
                    Matrix_Big[i, j] = Matrix[i, j];
                    Matrix_Big[i, j + n] = xirtaM[i, j];
                }

            //Прямой ход (Зануление нижнего левого угла)
            for (int k = 0; k < n; k++) //k-номер строки
            {
                for (int i = 0; i < 2*n; i++) //i-номер столбца
                    Matrix_Big[k, i] = Matrix_Big[k, i] / Matrix[k, k]; //Деление k-строки на первый член !=0 для преобразования его в единицу
                for (int i = k + 1; i < n; i++) //i-номер следующей строки после k
                {
                    double K = Matrix_Big[i, k] / Matrix_Big[k, k]; //Коэффициент
                    for (int j = 0; j < 2*n; j++) //j-номер столбца следующей строки после k
                        Matrix_Big[i, j] = Matrix_Big[i, j] - Matrix_Big[k, j] * K; //Зануление элементов матрицы ниже первого члена, преобразованного в единицу
                }
                for (int i = 0; i < n; i++) //Обновление, внесение изменений в начальную матрицу
                    for (int j = 0; j < n; j++)
                        Matrix[i, j] = Matrix_Big[i, j];
            }

            //Обратный ход (Зануление верхнего правого угла)
            for (int k = n - 1; k > -1; k--) //k-номер строки
            {
                for (int i = 2*n - 1; i > -1; i--) //i-номер столбца
                    Matrix_Big[k, i] = Matrix_Big[k, i] / Matrix[k, k];
                for (int i = k - 1; i > -1; i--) //i-номер следующей строки после k
                {
                    double K = Matrix_Big[i, k] / Matrix_Big[k, k];
                    for (int j = 2*n - 1; j > -1; j--) //j-номер столбца следующей строки после k
                        Matrix_Big[i, j] = Matrix_Big[i, j] - Matrix_Big[k, j] * K;
                }
            }

            //Отделяем от общей матрицы
            for (int i = 0; i < n; i++)
                for (int j = 0; j < n; j++)
                    xirtaM[i, j] = Matrix_Big[i, j + n];

            return xirtaM;        
        }
    }
}

Примечания

Литература

• Atkinson, Kendall A. (1989), An Introduction to Numerical Analysis (2nd ed.), New York: John Wiley & Sons , ISBN 978-0471624899 .
• Bolch, Gunter; Greiner, Stefan; de Meer, Hermann; Trivedi, Kishor S. (2006), Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications (2nd ed.), , ISBN 978-0-471-79156-0 .
• Calinger, Ronald (1999), A Contextual History of Mathematics , Prentice Hall , ISBN 978-0-02-318285-3 .
• Farebrother, R.W. (1988), Linear Least Squares Computations , STATISTICS: Textbooks and Monographs, Marcel Dekker, ISBN 978-0-8247-7661-9
• (2002), Accuracy and Stability of Numerical Algorithms (2nd ed.), , ISBN 978-0-89871-521-7 .
• Katz, Victor J. (2004), A History of Mathematics, Brief Version , Addison-Wesley , ISBN 978-0-321-16193-2 .
• Lipson, Marc; Lipschutz, Seymour (2001), Schaum's outline of theory and problems of linear algebra , New York: McGraw-Hill , pp. 69—80, ISBN 978-0-07-136200-9 .
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), , Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8

Ссылки

• (англ.)
• Kaw, Autar; Kalu, Egwu (неопр.) . University of South Florida (2010).