Interested Article - Задача про мышей

- 2020-01-20
- 2



Задача про мышей — математическая головоломка , по условию которой несколько мышей (или комаров, собак, ракет), расположены в углах правильного многоугольника . Каждая мышь начинает двигаться в направлении ближайшего соседа (по часовой стрелке или против часовой стрелки). В задаче требуется определить момент времени, когда мыши встретятся.
Наиболее распространённый вариант задачи — когда мыши начинают двигаться из углов единичного квадрата, причём скорость мышей одинакова. В этом случае все они встречаются в один и тот же момент времени, поскольку расстояние между двумя соседними мышами всегда уменьшается, а скорость постоянна. В общем, для правильного многоугольника с n сторонами, расстояние между соседними мышами уменьшается со скоростью 1 − cos(2π/ n ), и таким образом, они встретятся через время 1/(1 − cos(2π/ n )) .
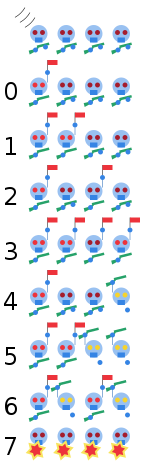
Траектория мышей
Для всех правильных многоугольников мыши двигаются по логарифмической спирали , которая сходится в центре многоугольника . При увеличении количества мышей, и если мыши движутся в направлении не своих ближайших соседей, определить их траектории сложнее.


См. также
Примечания
- Гамов, Георгий Антонович , Штерн, Марвин (1958), Математическая головоломка, Нью-Йорк: Viking press, с. 112—114
- Эдвард Лукас, (1877), «Задача про трёх собак», Nouv. Corresp. Math. 3: с. 175—176
- . MathWorld . Дата обращения: 23 апреля 2015. 13 апреля 2015 года.
Ссылки
- [ неавторитетный источник ] — расширенная задача про мышей.
- 2020-01-20
- 2