Серединный перпендикуляр (также срединный перпендикуляр и устаревший термин медиатриса ^{[ источник не указан 2104 дня ]} ) — прямая , перпендикулярная данному отрезку и проходящая через его середину .

Свойства

• Серединные перпендикуляры к сторонам треугольника (или другого многоугольника, для которого существует описанная окружность) пересекаются в одной точке — центре описанной окружности . У остроугольного треугольника эта точка лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
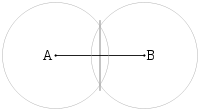
• Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
  • Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
• В равнобедренном треугольнике высота, биссектриса и медиана, проведенные из вершины угла с равными сторонами, совпадают и являются серединным перпендикуляром, проведённым к основанию треугольника, а два других серединных перпендикуляра равны между собой.
• Отрезки серединных перпендикуляров к сторонам треугольника, заключённые внутри него, можно найти по следующим формулам :

${\displaystyle p_{a}={\frac {2aS}{a^{2}+b^{2}-c^{2}}},\;\;p_{b}={\frac {2bS}{a^{2}+b^{2}-c^{2}}},\;\;p_{c}={\frac {2cS}{a^{2}-b^{2}+c^{2}}},}$

где нижний индекс обозначает сторону, к которой проведён перпендикуляр, ${\displaystyle S}$ — площадь треугольника, а также предполагается, что стороны связаны неравенствами ${\displaystyle a\geqslant b\geqslant c.}$

• Если стороны треугольника удовлетворяют неравенствам ${\displaystyle a\geq b\geq c}$ , тогда справедливы неравенства :

${\displaystyle p_{a}\geq p_{b}}$ и ${\displaystyle p_{c}\geq p_{b}.}$ Иными словами, наименьшим является серединный перпендикуляр, проведенный к стороне с промежуточной длиной.

Вариации и обобщения

• Окружность Аполлония — геометрическое место точек плоскости, отношение расстояний от которых до двух заданных точек — величина постоянная.

Примечания

Литература

• .