Interested Article - Центроид треугольника

- 2021-03-04
- 1
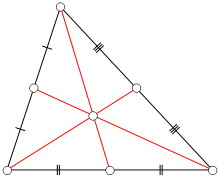
Центроид треугольника (также барицентр треугольника и центр тяжести треугольника ) — точка пересечения медиан в треугольнике .
Центроид традиционно обозначается латинской буквой . Центроид треугольника относится к замечательным точкам треугольника и он перечислен в энциклопедии центров треугольника Кларка Кимберлинга , как точка X(2).
Свойства
- Центроид делит каждую медиану в отношении 2:1, считая от вершины.
- Центроид лежит на отрезке, соединяющем ортоцентр и центр описанной окружности, и делит его в отношении 2:1 (см. прямая Эйлера ).
- Если в вершины треугольника поместить равные массы, то центр масс ( барицентр ) полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой внутри массой также находится в центроиде.
-
Если
— центроид треугольника
то для любой точки
верно равенство
- .
- Центроид является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение ( теорема Лейбница ).
- Три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника (равной площади).
- Три отрезка прямых, соединяющих середины сторон треугольника с центроидом, разбивают данный треугольник на три равновеликих четырёхугольника (равной площади).
- При изогональном сопряжении центроид переходит в точку Лемуана (в точку пересечения трех симедиан треугольника).
- Построим две прямые, каждая из которых проходит через точку Аполлония и точку Торричелли , отличную от изогонально сопряжённой ей. Такие прямые пересекутся в центроиде треугольника.
- Пусть — треугольник на плоскости. Окружность, проходящая через центроид и две точки Аполлония треугольника , называется окружностью Парри треугольника .
- Три чевианы , проведённые через произвольную точку внутри треугольника, делят своими концами стороны треугольника на шесть отрезков. Произведение длин трёх из этих шести отрезков, не имеющих общих концов, максимально, если точка совпадает с центроидом .
- Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин:
- .
- Пусть , и — расстояния от центроида до сторон с длинами, соответственно равными , и . Тогда :173
- и
- ,
- где — площадь треугольника.
История
Факт того, что три медианы пересекаются в одной точке, был доказан ещё Архимедом .
Вариации и обобщения. Центроиды в четырёхугольнике
- Центроид ( барицентр или центр масс ) произвольного четырёхугольника лежит в точке пересечения средних линий четырёхугольника и отрезка, соединяющего середины диагоналей, и делит все три отрезка пополам.
-
Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершины
- Если во вписанном в окружность четырёхугольнике провести диагональ, а в полученные два треугольника вписать две окружности, затем аналогично поступить, проведя вторую диагональ, тогда центроиды этих четырёх треугольников лежат на одной окружности .
- У выпуклого четырёхугольника, вписанного в окружность, «центроид площади» или центр масс его площади G a , вершинный центроид или центр масс четырёх его вершин G v и точка пересечения его диагоналей P коллинеарны. Расстояния между этими точками удовлетворяют формуле
См. также
- Барицентр
- Центр тяжести
- Центр масс
- Ортоцентр
- Инцентр
- Замечательные точки треугольника
- Геометрия треугольника
Примечания
- Е. Смирнова. . — Litres, 2017-09-05. — С. 165. — 417 с.
- , с. 12.
- , pp. 70–71)
- Johnson, Roger A., Advanced Euclidean Geometry , Dover Publ. Co., 2007
- Andreescu, Titu; Enescu, Bogdan (2004), , Mathematical Olympiad Treasures , Springer, pp. 44—46, 50, ISBN 978-0-8176-4305-8 , MR
- Bradley, Christopher (2011), (PDF) , (PDF) из оригинала 17 января 2021 , Дата обращения: 27 апреля 2016
Литература
- Понарин Я. П. Элементарная геометрия. В 2 т. — М. : МЦНМО , 2004. — С. 80-81. — ISBN 5-94057-170-0 .
- Дм. Ефремов. 1902 год
- Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М: Учпедгиз, 1962. 153 с.
- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble , LCCN
- 2021-03-04
- 1