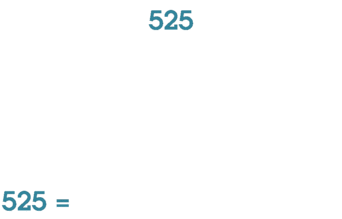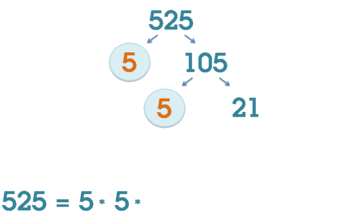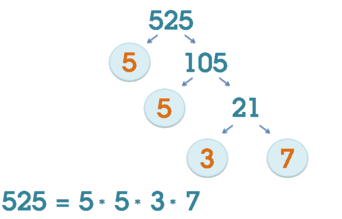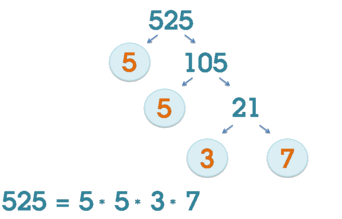В математике факториза́ция — это декомпозиция объекта (например, числа , полинома или матрицы ) в произведение других объектов, или факторов , которые, будучи перемноженными , дают исходный объект. Например, число 15 факторизуется на простые числа 3 и 5, а полином x ² − 4 факторизуется на ( x − 2)( x + 2). В результате факторизации во всех случаях получается произведение более простых объектов, чем исходный.

Целью факторизации является приведение объекта к «основным строительным блокам», например, число к простым числам, многочлен — к неприводимым многочленам . Факторизация целых чисел обеспечивается основной теоремой арифметики , а многочленов — основной теоремой алгебры .

Противоположностью факторизации полиномов является их , перемножение полиномиальных факторов для получения «расширенного» многочлена, записанного в виде суммы слагаемых.

Факторизация целых чисел для больших чисел является задачей большой сложности. Не существует никакого известного способа, чтобы решить эту задачу быстро. Её сложность лежит в основе некоторых алгоритмов шифрования с открытым ключом , таких как RSA .

Матрица может также быть факторизована на произведение матриц специального вида для приложений, в которых эта форма удобна. Одним из основных примеров этого является использование ортогональных , унитарных и треугольных матриц. Существуют различные способы факторизации: QR-разложение , LQ , QL , RQ , RZ .

Ещё одним примером является факторизация функций в виде композиции других функций, имеющих определённые свойства. Например, каждая функция может рассматриваться как композиция сюръективной функции с инъективной . Этот подход является обобщением понятия факторизации систем.

Наконец, в теории графов факторизация графа определяется как разложение графа на непересекающиеся по рёбрам остовные подграфы (то есть подграфы, содержащие все вершины графа) специального вида .

Целые числа

По основной теореме арифметики каждое натуральное число имеет единственное разложение на простые множители. Существует множество алгоритмов факторизации целого, с помощью которых можно факторизовать любое натуральное число до состава его простых множителей с помощью рекуррентных формул . Однако, для очень больших чисел эффективный алгоритм пока неизвестен.

Гауссовы числа

Кольцо гауссовых чисел факториально , то есть разложение на простые множители однозначно с точностью до их порядка и ассоциированности (умножения на делители единицы ).

Многочлены

См. также

• Факторизация отображений
• Разложение матрицы
• Факториальное кольцо
• Wolfram Alpha

Примечания

Ссылки

• Л. Инфельд, Т. Е. Хал
• is an online factorization tool.