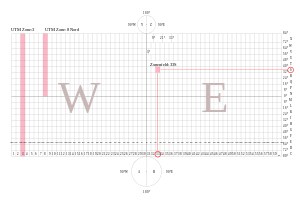
Равноуго́льная цилиндри́ческая прое́кция Мерка́тора — одна из основных картографических проекций . Разработана Герардом Меркатором для применения в его «Атласе». « Равноугольная » в названии проекции подчёркивает то, что проекция сохраняет углы между направлениями. Все локсодромы в ней изображаются прямыми линиями. Меридианы в проекции Меркатора представляются параллельными равноотстоящими линиями. Параллели же представляют собой параллельные линии, расстояние между которыми вблизи экватора равно расстоянию между меридианами и быстро увеличивается при приближении к полюсам . Сами полюсы не могут быть изображены на проекции Меркатора (это обусловлено особенностями функции, отображающей координаты на сфере на координаты на плоскости), поэтому обычно карту в проекции Меркатора ограничивают областями до 80—85° северной и южной широты .

Масштаб на карте в этой проекции не является постоянным, он увеличивается от экватора к полюсам (как обратный косинус широты), однако масштабы по вертикали и по горизонтали всегда равны, чем, собственно, и достигается равноугольность проекции. На картах в данной проекции всегда указывается, к какой параллели относится основной масштаб карты.

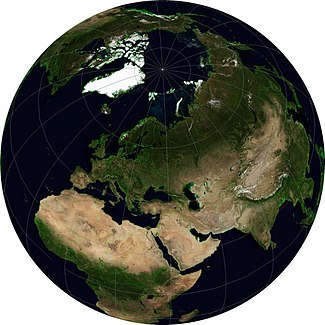
Поскольку проекция Меркатора имеет различный масштаб на разных участках, эта проекция не сохраняет площади. Если основной масштаб относится к экватору, то наибольшие искажения размеров объектов будут у полюсов. Это хорошо заметно на картах в этой проекции: на них Гренландия кажется в 2—3 раза больше Австралии и сравнима по размерам с Южной Америкой . В реальности Гренландия втрое меньше Австралии и в 8 раз меньше Южной Америки.

Проекция Меркатора оказалась весьма удобной для нужд мореходства, особенно в старые времена. Объясняется это тем, что траектория движения корабля, идущего под одним и тем же румбом к меридиану (то есть с неизменным положением стрелки компаса относительно шкалы) изображается прямой линией на карте в проекции Меркатора.

Математическое выражение проекции Меркатора

Для начала рассмотрим простейший вариант проекции Меркатора: проекцию сферы на цилиндр. Этот вариант не учитывает сплюснутости Земли у полюсов. Цилиндричность проекции сразу даёт нам выражение для горизонтальной координаты на карте: она просто пропорциональна долготе точки ${\displaystyle \lambda }$ (при использовании в расчетах следует учесть, что выражаться эта величина должна в радианах):

${\displaystyle x=c(\lambda -\lambda _{0}).}$

Условие равноугольности — это просто равенство масштабов по горизонтальной и вертикальной оси. Поскольку масштаб по оси X на широте ${\displaystyle \theta }$ равен просто ${\displaystyle c/(R\cos \theta )}$ ( R — радиус Земли), то из условия ${\displaystyle dyR\cos \theta /c=Rd\theta }$ мы получаем выражение для зависимости y от ${\displaystyle \theta }$ :

${\displaystyle {\begin{matrix}y&=&c\ln \operatorname {tg} \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)\\&=&c\,\operatorname {arth} \sin \theta .\end{matrix}}}$

(Здесь arth — обратный гиперболический тангенс ).

Функция ${\displaystyle \operatorname {arth} \sin \theta }$ носит специальное название функции Ламберта, или ламбертиана (в честь Иоганна Ламберта ) и иногда обозначается как ${\displaystyle \operatorname {lam} \theta }$ или ${\displaystyle \operatorname {arcgd} \theta }$ (см. также Интеграл от секанса ).

Обратное преобразование (из линейной координаты y в широту θ ) носит название функции Гудермана , или гудерманиана (в честь Кристофа Гудермана ) и обозначается ${\displaystyle \operatorname {gd} y.}$ Обратное преобразование координаты x в долготу λ является, как и прямое преобразование, линейной функцией:

${\displaystyle {\begin{matrix}\theta &=&\operatorname {gd} y=2\operatorname {arctg} \left(e^{y/c}\right)-{\frac {1}{2}}\pi \\\\\ &=&\operatorname {arctg} \left(\operatorname {sh} (y/c)\right),\\\\\lambda &=&x/c+\lambda _{0}.\end{matrix}}}$

Теперь нетрудно получить выражения для равноугольной проекции с учётом эллипсоидальной формы Земли. Для этого надо записать для эллипсоида ( a — большая полуось , b — малая полуось) в географических координатах

${\displaystyle dl^{2}={\frac {a^{2}d\lambda ^{2}}{1+{\frac {a^{2}}{b^{2}}}\operatorname {tg} ^{2}\theta }}+{\frac {b^{4}}{a^{2}}}{\frac {d\theta ^{2}}{(\cos ^{2}\theta +{\frac {b^{2}}{a^{2}}}\sin ^{2}\theta )^{3}}},}$

перейти в ней к координатам x и y и приравнять масштабы по осям. После интегрирования получаем

${\displaystyle {\begin{matrix}x&=&c(\lambda -\lambda _{0})\\y&=&c[\operatorname {arth} \sin \theta -\varepsilon \operatorname {arth} (\varepsilon \sin \theta )].\end{matrix}}}$

Здесь ${\displaystyle \varepsilon ={\sqrt {a^{2}-b^{2}}}/a}$ — эксцентриситет земного эллипсоида .

Обратное преобразование, вообще говоря, не выражается в элементарных функциях , но уравнение для обратного преобразования легко решить методом теории возмущений по малому ${\displaystyle \varepsilon }$ . Итерационная формула для обратного преобразования имеет следующий вид:

${\displaystyle \theta _{n+1}=f\left(\theta _{n},y\right)}$ , где ${\displaystyle \theta _{0}}$ можно взять равным 0 или приближению, рассчитанному по формуле для сфероида.

${\displaystyle \theta _{n+1}=\arcsin \left(1-{\frac {(1+\sin \theta _{n})(1-\varepsilon \sin \theta _{n})^{\varepsilon }}{e^{\frac {2y}{c}}(1+\varepsilon \sin \theta _{n})^{\varepsilon }}}\right)}$

См. также

• Dell'Arcano del Mare

Ссылки