Уравнение Фоккера — Планка — одно из дифференциальных уравнений в частных производных, описывает временну́ю эволюцию функции плотности вероятности координат и импульса частиц в процессах, где важна стохастическая природа явления . Названо в честь нидерландского и немецкого физиков Адриана Фоккера и Макса Планка , также известно как прямое уравнение Колмогорова . Может быть обобщено на другие измеримые параметры: размер (в теории коалесценции ), масса и т. д.

Определение

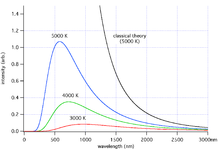
Впервые уравнение было использовано для статистического описания броуновского движения частиц в воде. Хотя броуновское движение описывается уравнениями Ланжевена , которые могут быть решены численно методом Монте-Карло или методами молекулярной динамики , задачу в такой постановке часто трудно решить аналитически. И, вместо сложных численных схем, можно ввести функцию плотности вероятности ${\displaystyle W(\mathbf {v} ,\;t)}$ , описывающую вероятность того, что частица имеет скорость в интервале ${\displaystyle (\mathbf {v} ,\;\mathbf {v} +d\mathbf {v} )}$ , если в момент времени 0 она имела начальную скорость ${\displaystyle \mathbf {v} _{0}}$ , и записать для ${\displaystyle W(\mathbf {v} ,\;t)}$ уравнения Фоккера — Планка.

Общая форма уравнения Фоккера — Планка для ${\displaystyle N}$ переменных:

${\displaystyle {\frac {\partial W}{\partial t}}=\left[-\sum _{i=1}^{N}{\frac {\partial }{\partial x_{i}}}D_{i}^{1}(x_{1},\;\ldots ,\;x_{N})+\sum _{i=1}^{N}\sum _{j=1}^{N}{\frac {\partial ^{2}}{\partial x_{i}\partial x_{j}}}D_{ij}^{2}(x_{1},\;\ldots ,\;x_{N})\right]W,}$

где ${\displaystyle D^{1}}$ — вектор сноса и ${\displaystyle D^{2}}$ — тензор диффузии , причём диффузия вызвана действием сил стохастической природы.

Связь со стохастическими дифференциальными уравнениями

Уравнение Фоккера — Планка может быть использовано для расчёта плотности вероятности в стохастических дифференциальных уравнениях . Рассмотрим следующее стохастическое дифференциальное уравнение

${\displaystyle d\mathbf {X} _{t}={\boldsymbol {\mu }}(\mathbf {X} _{t},\;t)\,dt+{\boldsymbol {\sigma }}(\mathbf {X} _{t},\;t)\,d\mathbf {B} _{t},}$

где ${\displaystyle \mathbf {X} _{t}\in \mathbb {R} ^{N}}$ — функция состояния системы, а ${\displaystyle \mathbf {B} _{t}\in \mathbb {R} ^{M}}$ — стандартное ${\displaystyle N}$ -мерное броуновское движение . Если начальное распределение задано как ${\displaystyle \mathbf {X} _{0}\sim W(\mathbf {x} ,\;0)}$ , то плотность вероятности ${\displaystyle W(\mathbf {x} ,\;t)}$ состояния системы ${\displaystyle \mathbf {X} _{t}}$ является решением уравнения Фоккера — Планка со следующими выражениями для сноса и диффузии соответственно:

${\displaystyle D_{i}^{1}(\mathbf {x} ,\;t)=\mu _{i}(\mathbf {x} ,\;t),}$

${\displaystyle D_{ij}^{2}(\mathbf {x} ,\;t)={\frac {1}{2}}\sum _{k}\sigma _{ik}(\mathbf {x} ,\;t)\sigma _{jk}(\mathbf {x} ,\;t).}$

Пример

Стандартное скалярное уравнение броуновского движения генерируется следующим стохастическим дифференциальным уравнением:

${\displaystyle \mathrm {d} X_{t}=\mathrm {d} B_{t}.\ }$

Здесь скорость сноса равна нулю и коэффициент диффузии равен 1/2, следовательно, соответствующее уравнение Фоккера — Планка выглядит так:

${\displaystyle {\frac {\partial W(x,\;t)}{\partial t}}={\frac {1}{2}}{\frac {\partial ^{2}W(x,\;t)}{\partial x^{2}}},}$

это простейшая форма одномерного уравнения диффузии ( теплопереноса ).

Уравнение Фоккера — Планка в одномерном случае

В одномерном случае УФП приобретает вид:

${\displaystyle {\frac {\partial f}{\partial t}}=-{\frac {\partial }{\partial x}}(A(x,\;t)f(x,\;t))+{\frac {\partial }{\partial x}}\left({\frac {B(x,\;t)}{2}}{\frac {\partial }{\partial x}}f(x,\;t)\right).}$

УФП справедливо для условной плотности вероятности:

${\displaystyle f(x,\;t)=p(x,\;t|x_{0},\;t_{0}),}$ (то есть значение функции ${\displaystyle f(x,\;t)}$ вероятностно попадает в плоскость, образованную пространственной осью ${\displaystyle x\ }$ и временно́й осью ${\displaystyle t\ }$ , в интервалы ${\displaystyle x-x_{0}\ }$ и ${\displaystyle t-t_{0}\ }$ соответственно) при любом начальном значении ${\displaystyle x_{0}\ }$ и ${\displaystyle t_{0}\ }$ и начальном условии ${\displaystyle p(x,\;t_{0}|x_{0},\;t_{0})=\delta (x-x_{0})}$ , где ${\displaystyle \delta (x-x_{0})\ }$ — функция Дирака.

Это условие гласит, что в один и тот же момент времени ${\displaystyle t_{0}\ }$ функция претерпевает скачок. Если пространственные координаты равны, то функция устремляется в бесконечность. Поэтому, в силу ограниченности функции, необходимо использовать определение единовременной плотности вероятности ${\displaystyle p(x,\;t)=\int p(x,\;t;\;x_{0},\;t_{0})\,dx_{0}=\int p(x,\;t|x_{0},\;t_{0})p(x_{0},t_{0})\,dx_{0}.}$ Тогда, УФП справедливо для вероятности ${\displaystyle p(x,\;t)}$ с начальным условием ${\displaystyle p(x,\;t)|_{t=t_{0}}=p(x,\;t_{0})}$ , которое менее сингулярно, чем ${\displaystyle p(x,\;t_{0}|x_{0},\;t_{0})=\delta (x-x_{0})}$ . Стохастический процесс, описываемый условной вероятностью, удовлетворяющий УФП, эквивалентен СДУ Ито

${\displaystyle dx(t)=A(x(t),\;t)\,dt+{\sqrt {B(x(t),\;t)}}\,dW(t)}$

и что эти два описания должны рассматриваться как взаимно дополняющие друг друга.

Вывод

Первый согласованный вывод уравнения Фоккера — Планка на основе точной микроскопической динамики для классических и квантовых систем выполнен Н. Н. Боголюбовым и Н. М. Крыловым (переиздано в ).

См. также

• Цепочка уравнений Боголюбова
• Уравнение Лиувилля
• Уравнение Больцмана
• Уравнение Власова
• Уравнение Колмогорова — Чепмена
• Уравнения Навье — Стокса
• Формула Фейнмана — Каца

Примечания

Литература

• Risken H. The Fokker — Planck Equation: Methods of Solutions and Applications. — 2nd ed. — Springer, 1984. — 452 p. — ISBN 3-540-61530-X .
• Лифшиц Е. М., Питаевский Л. П. Физическая кинетика. — М. : Наука , 1979 . — 528 с. — («Теоретическая физика», том X). — 50 000 экз.