Interested Article - Космологическое уравнение состояния

- 2020-08-18
- 2
Космологическое уравнение состояния ( уравнение состояния космологической модели ) — зависимость давления от плотности энергии определённой среды . В космологии принимают, что давление зависит линейно от плотности энергии : Уравнение состояния определяет, как со временем происходит расширение Вселенной и изменение плотности энергии самой среды. Для нерелятивисткого вещества безразмерные коэффициент пропорциональности для излучения и релятивистских частиц Среда с уравнением состояния, для которого приводит к ускорению расширения Вселенной и называется тёмной энергией; наиболее общепринятым вариантом тёмной энергии является космологическая постоянная с
Описание
Уравнения состояния в общем виде могут иметь сложный вид, но поскольку космология обычно имеет дело с разреженными средами, то зависимость давления от плотности энергии представляют в линейном виде: , где ― безразмерная величина .
Уравнение состояния различных сред во Вселенной и их плотность — параметры, от которых зависит расширение Вселенной. Его можно описать следующими уравнениями :
Уравнение ускорения:
Третье уравнение выводится из первых двух, так что в этой системе два независимых уравнения . В этих уравнениях — масштабный коэффициент ― величина, описывающая расширение или сжатие Вселенной, — гравитационная постоянная , — скорость света , — кривизна Вселенной (принимает значения для плоского пространства, для пространства с положительной кривизной и с отрицательной), ― радиус кривизны Вселенной. Точка или две точки над символом означает, соответственно, производную по времени или производную второго порядка по времени .
В этих уравнениях три неизвестных функции от времени: , , . Уравнение состояния даёт связь между двумя последними неизвестными, что позволяет решить систему уравнений. От его типа зависит вид решения. Например, у сред с различными коэффициентами плотность энергии при расширении Вселенной меняется по-разному: из закона сохранения можно получить соотношение При этом среды с различными уравнениями состояния могут сосуществовать одновременно: если между ними не происходит обмен энергией, то при расширении Вселенной плотность энергии каждой из сред меняется независимо от остальных . Для Вселенной с нулевой кривизной, содержащей только среду с определённым уравнением состояния, функция также будет зависеть от :
где — возраст Вселенной в данный момент. Для такой однокомпонентной Вселенной возраст можно выразить через и постоянную Хаббла в момент :
В этом же случае плотность энергии меняется со временем как независимо от . Приведённые формулы справедливы для .
Можно рассмотреть обычное нерелятивистское вещество. Давление в нём пренебрежимо мало по сравнению с плотностью энергии (см. ниже ), так что . Если вся Вселенная состоит из обычного вещества, то при расширении Вселенной и росте плотность энергии такого вещества уменьшается, как следует из закона сохранения. Уравнение ускорения показывает, что то есть, расширение Вселенной замедляется — это можно упрощённо интерпретировать как простое следствие гравитационного взаимодействия , которое замедляет разлёт частиц. Если же представить , то это будет означать, что при положительной плотности энергии, наоборот, Вселенная расширяется ускоренно ― это случай тёмной энергии (см. ниже ) .
Уравнения состояния различных сред

Материя
В качестве примера можно рассмотреть разреженный газ, состоящий из нерелятивистских частиц. Уравнение состояния идеального газа обычно записывают в следующем виде :
где — массовая плотность , — молярная масса газа, — постоянная Больцмана , — температура . Чтобы перейти к выражению давления через плотность энергии, нужно учесть, что у нерелятивистского газа энергия практически равна энергии покоя , так что Тогда можно записать :
Поскольку газ нерелятивистский, то для среднеквадратичной скорости его частиц верно соотношение , где предполагается Уравнение состояния можно привести к виду где :
Таким образом, для нерелятивистского вещества можно считать Среду с таким уравнением состояния в космологии принято называть холодной материей, либо просто материей, противопоставляя ей излучение (см. ниже ). К ней относится не только нерелятивистское барионное вещество , сейчас составляющее 4,8 % критической плотности Вселенной , но и холодная тёмная материя — принятый в стандартной модели ΛCDM вид тёмной материи , которая составляет 26 % критической плотности и имеет неизвестную природу .
Для частично релятивистского вещества, у которого будет находиться в диапазоне от 0 до 1/3 .
Излучение
Уравнение состояния для фотонов , а также для релятивистского газа записывается в виде :
Соответственно, Среду с таким уравнением состояния в космологии принято называть горячей материей, либо излучением. В современной Вселенной плотность излучения очень мала: фотоны, в основном относящиеся к реликтовому излучению , составляют 5,4⋅10 −5 критической плотности, а релятивистские нейтрино ― 3,6⋅10 −5 критической плотности. Из-за такого уравнения состояния плотность излучения убывает с расширением Вселенной как что быстрее, чем убывание плотности материи как Плотности материи и излучения были равны, когда Вселенной было 50 миллионов лет ― сейчас её возраст составляет 13,7 миллиардов лет .
Более быстрый спад плотности энергии излучения при расширении Вселенной можно интерпретировать следующим образом. Концентрация и для фотонов, и для нерелятивистских частиц меняется с масштабным коэффициентом как Для нерелятивистских частиц, энергия которых практически полностью обусловлена энергией покоя, такую же пропорциональность имеет и плотность энергии. Энергию фотона можно выразить через его длину волны : где — постоянная Планка . Поскольку длина волны фотона увеличивается вместе с расширением Вселенной — , то для фотонов .
Кривизна пространства
Кривизну пространства также можно представить в виде составляющей Вселенной и использовать плотность кривизны в уравнениях, описывающих расширение Вселенной. Для кривизны и Плотность кривизны точно определяется через радиус кривизны :
Наблюдения показывают, что наша Вселенная практически плоская, с радиусом кривизны гораздо большим, чем радиус горизонта , и плотность кривизны считают нулевой .
Тёмная энергия
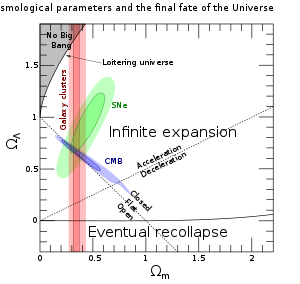
Различные среды с уравнениями состояния, для которых , называют тёмной энергией . Особенность такого уравнения состояния в том, что при положительной плотности тёмной энергии уравнение ускорения даёт что означает ускоренное расширение Вселенной . Тёмная энергия имеет неизвестную природу, но поскольку ускоренное расширение Вселенной наблюдается в действительности, тёмная энергия — необходимая составляющая Вселенной .
Наиболее общепринятый вариант тёмной энергии — космологическая постоянная (лямбда-член) с При таком уравнении состояния плотность тёмной энергии остаётся постоянной при расширении Вселенной, поэтому космологическую постоянную также интерпретируют как энергию вакуума . Плоская Вселенная, в которой доминирует космологическая постоянная, будет расширяться экспоненциально: .
В модели ΛCDM используется именно этот вид тёмной энергии, её плотность составляет 69 % критической плотности. В возрасте Вселенной в 10,2 миллиарда лет доли материи и космологической постоянной во Вселенной были равны. Кроме того, космологическая постоянная — исторически первый рассмотренный вид тёмной энергии: первоначально Альберт Эйнштейн ввёл его для построения модели в 1917 году .
Тем не менее, не исключены и другие уравнения состояния тёмной энергии. Например, возможный вариант тёмной энергии с называется фантомной энергией — при расширении её плотность энергии возрастает. Если в расширяющейся Вселенной присутствует фантомная энергия, то её плотность рано или поздно будет превышать плотность энергии любых гравитационно связанных систем и других тел, что приведёт к их разрушению, а масштабный коэффициент достигнет бесконечности за конечное время — это сценарий Большого разрыва .
Также не исключена и возможность того, что тёмной энергии меняется со временем — подобный вид тёмной энергии называют квинтэссенцией .
Примечания
- ↑ , p. chapter 4.4.
- ↑ , с. 59.
- , p. chapters 1, 2.3, 3.4, 4.
- , с. 29.
- , p. chapters 4.4, 5.3.
- ↑ , p. chapter 5.3.
- , p. chapters 4.2, 4.4.
- , с. 78.
- . www.sciencedirect.com . Дата обращения: 9 января 2023. 9 января 2023 года.
- ↑ , p. chapters 4.4, 5.5, 11.5.
- . astronomy.swin.edu.au . Дата обращения: 9 января 2023. 9 января 2023 года.
- . astronomy.swin.edu.au . Дата обращения: 10 января 2023. 9 января 2023 года.
- , p. chapters 4.4, 5.5.
- , p. chapter 5.1.
- ↑ Hu W. . University of Chicago . Дата обращения: 10 января 2023. 10 января 2023 года.
- , p. chapter 6.2.
- . astronomy.swin.edu.au . Дата обращения: 10 января 2023. 6 ноября 2022 года.
- , p. chapters 4.4, 4.5, 5.3.3.
- , p. chapters 4.5, 5.5, 11.5.
- , pp. chapters 5, 12 exercises.
- Tsujikawa S. // Classical and Quantum Gravity. — 2013-11-01. — Т. 30 . — С. 214003 . — ISSN . — doi : . 28 ноября 2022 года.
Литература
- Вайнберг С. . — М. : УРСС , 2013. — 608 с. — ISBN 978-5-453-00040-1 .
- Ryden B. . — Cambridge University Press, 2017. — 277 с. — ISBN 978-1-107-15483-4 .
- 2020-08-18
- 2