Interested Article - Тензор Риччи

- 2020-05-12
- 1
Тензор Риччи , названный в честь итальянского математика Грегорио Риччи-Курбастро , задаёт один из способов измерения кривизны многообразия , то есть степени отличия геометрии многообразия от геометрии плоского евклидова пространства . Тензор Риччи, точно так же как метрический тензор , является симметричной билинейной формой на касательном пространстве риманова многообразия . Грубо говоря, тензор Риччи измеряет деформацию объёма , то есть степень отличия n -мерных областей n -мерного многообразия от аналогичных областей евклидова пространства (см. тензора Риччи). Обычно обозначается или .
Определение
Пусть — n- мерное риманово многообразие , а — касательное пространство к M в точке p . Для любой пары касательных векторов в точке p , тензор Риччи , по определению, отображает в след линейного автоморфизма , заданного тензором кривизны Римана R :
Если на многообразии заданы локальные координаты, то тензор Риччи можно разложить по компонентам:
где — след тензора Римана в координатном представлении.
Геометрический смысл
В окрестности любой точки p риманова многообразия можно всегда определить специальные локальные координаты, так называемые , в которых геодезические из точки p совпадают с прямыми, проходящими через начало координат. Кроме того, в самой точке p метрический тензор равен метрике евклидова пространства (или метрике Минковского в случае псевдориманова многообразия ).
В этих специальных координатах форма объема раскладывается в ряд Тейлора вокруг p :
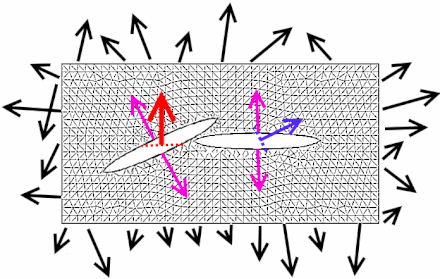
Таким образом, если кривизна Риччи положительна в направлении вектора , то узкий конус геодезических, исходящих из точки p в направлении , будет иметь меньший объем, чем такой же конус в евклидовом пространстве. Аналогично, если кривизна Риччи отрицательна, то узкий конус геодезических в направлении вектора будет иметь объем, больший по сравнению с евклидовым.
Кривизна Риччи и геометрия в целом
Пусть есть полное -мерное риманово многообразие с
-
Неравенство Бишопа — Громова
. Пусть
, обозначим через
объём
шара радиуса
с центром в
, обозначим через
объём шара радиуса
в
-мерном пространстве постоянной кривизны
. Тогда отношение
- есть невозрастающая функция от .
- Теорема Мейера
- Из тождества Бохнера для 1-форм следует, что если то собственные числа лапласиана на не меньше чем у единичной -мерной сферы.
Приложения тензора Риччи
- Тензор кривизны Риччи в общей теории относительности служит ключевым компонентом уравнений Эйнштейна .
- Кривизна Риччи также появляется в уравнении потока Риччи , в котором зависящая от времени метрика деформируется пропорционально кривизне Риччи со знаком минус.
См. также
- 2020-05-12
- 1














![{\displaystyle d\mu _{g}={\Big [}1-{\frac {1}{6}}R_{jk}x^{j}x^{k}+O(|x|^{3}){\Big ]}d\mu _{\text{Евклида}}}](/images/008/662/8662868/15.jpg?rand=402427)