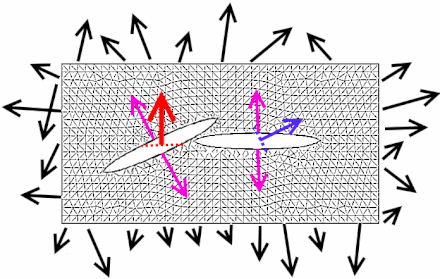
Тензор напряжений Максвелла
(назван в честь
Джеймса Клерка Максвелла
) представляет собой симметричный
тензор
второго порядка, используемый в
классическом электромагнетизме
для представления взаимодействия между электромагнитными силами и
механическим импульсом
. В простых случаях, таких как точечный заряд, свободно движущийся в однородном магнитном поле, легко рассчитать силы, действующие на заряд, согласно
силе Лоренца
. В более сложных случаях такая обычная процедура может стать непрактично сложной с уравнениями, охватывающими несколько строк. Поэтому удобно собрать многие из этих членов в тензоре напряжений Максвелла и использовать тензорную арифметику, чтобы найти ответ на поставленную задачу.
В релятивистской формулировке электромагнетизма тензор Максвелла появляется как часть
электромагнитного тензора энергии-импульса
, который является электромагнитной составляющей полного
тензора энергии-импульса
. Последний описывает плотность и поток энергии и импульса в
пространстве-времени
.
Обоснование
Ниже показано, что электромагнитная сила записывается параметрами
E
и
B.
Используя
векторное исчисление
и
уравнения Максвелла
, ищется симметрия в выражениях, содержащих
E
и
B
, а введение тензора напряжений Максвелла упрощает результат.
Уравнения Максвелла в единицах СИ в
вакууме
(для справки)
|
Имя
|
Дифференциальная форма
|
|
Закон Гаусса (в вакууме)
|

|
|
Закон Гаусса для магнетизма
|

|
Уравнение Максвелла – Фарадея
(закон индукции Фарадея)
|

|
Круговой закон Ампера (в вакууме)
(с поправкой Максвелла)
|

|
-
Согласно
силе Лоренца


сила на единицу объема равна

-
Далее,
ρ
and
J
могут быть заменены на электрическое и магнитное поля
E
and
B
, согласно
закону Гаусса
и
теореме Ампера о циркуляции магнитного поля
:

-
Производная по времени может быть переписана во что-то, что можно интерпретировать физически, а именно в
вектор Пойнтинга
. Использоваение
правила произведения
и
закона электромагнитной индукции Фарадея
дают:

и теперь мы можем перезаписать параметр
f
как

Затем, объединение с
E
и
B
даёт
![{\displaystyle \mathbf {f} =\varepsilon _{0}\left[({\boldsymbol {\nabla }}\cdot \mathbf {E} )\mathbf {E} -\mathbf {E} \times ({\boldsymbol {\nabla }}\times \mathbf {E} )\right]+{\frac {1}{\mu _{0}}}\left[-\mathbf {B} \times \left({\boldsymbol {\nabla }}\times \mathbf {B} \right)\right]-\varepsilon _{0}{\frac {\partial }{\partial t}}\left(\mathbf {E} \times \mathbf {B} \right).}](/images/008/662/8662876/12.jpg?rand=75182)
-
Выражение, по-видимому, «отсутствует» в симметрии в
E
and
B
, что может быть достигнуто путём вставки
(∇ ⋅
B
)
B
, ввиду
закона Гаусса для электромагнетизма
:
![{\displaystyle \mathbf {f} =\varepsilon _{0}\left[({\boldsymbol {\nabla }}\cdot \mathbf {E} )\mathbf {E} -\mathbf {E} \times ({\boldsymbol {\nabla }}\times \mathbf {E} )\right]+{\frac {1}{\mu _{0}}}\left[({\boldsymbol {\nabla }}\cdot \mathbf {B} )\mathbf {B} -\mathbf {B} \times \left({\boldsymbol {\nabla }}\times \mathbf {B} \right)\right]-\varepsilon _{0}{\frac {\partial }{\partial t}}\left(\mathbf {E} \times \mathbf {B} \right).}](/images/008/662/8662876/13.jpg?rand=922566)
Устранение вихрей (которые довольно сложно вычислить), используя
тождество векторного исчисления

приводит к:
![{\displaystyle \mathbf {f} =\varepsilon _{0}\left[({\boldsymbol {\nabla }}\cdot \mathbf {E} )\mathbf {E} +(\mathbf {E} \cdot {\boldsymbol {\nabla }})\mathbf {E} \right]+{\frac {1}{\mu _{0}}}\left[({\boldsymbol {\nabla }}\cdot \mathbf {B} )\mathbf {B} +(\mathbf {B} \cdot {\boldsymbol {\nabla }})\mathbf {B} \right]-{\frac {1}{2}}{\boldsymbol {\nabla }}\left(\varepsilon _{0}E^{2}+{\frac {1}{\mu _{0}}}B^{2}\right)-\varepsilon _{0}{\frac {\partial }{\partial t}}\left(\mathbf {E} \times \mathbf {B} \right).}](/images/008/662/8662876/15.jpg?rand=130235)
-
Это выражение содержит каждый аспект электромагнетизма и импульса и относительно легко вычисляется. Его можно записать более компактно, введя
тензор напряжений Максвелла
,

Всё, кроме последнего члена f, можно записать как
тензорную дивергенцию
тензора напряжений Максвелла, получая:

Как и в
теореме Пойнтинга
, второй член в правой части приведенного уравнения может быть интерпретирован как производная по времени от плотности импульса электромагнитного поля, в то время как первый член является производной по времени от плотности импульса для массивных частиц. Таким образом, приведённое выше уравнение будет законом сохранения импульса в классической электродинамике, где введён
вектор Пойнтинга

В приведённом выше соотношении сохранения импульса,
 является
плотностью потока импульса
и играет роль, аналогичную
является
плотностью потока импульса
и играет роль, аналогичную
 в
теореме Пойнтинга
.
в
теореме Пойнтинга
.
Приведённый выше вывод предполагает полное знание параметров
ρ
и
J
(как свободных, так и ограниченных зарядов и токов). В случае нелинейных материалов (таких как магнитное железо с BH-кривой (кривой плотности магнитного потока)) необходимо использовать нелинейный тензор напряжений Максвелла.
Уравнение
В
физике
тензор напряжений Максвелла
является тензором напряжений
электромагнитного поля
. Как указано выше в
единицах СИ
, это определяется как:
-

где ε
0
—
электрическая постоянная
, μ
0
—
магнитная постоянная
,
E
—
электрическое поле
,
B
—
магнитное поле
, а δ
ij
—
дельта Кронекера
. В гауссовых
единицах СГС
это определяется как:
-

где
H
—
намагничивающее поле
.
Альтернативный способ выражения этого тензора:
-
![{\displaystyle {\overset {\leftrightarrow }{\boldsymbol {\sigma }}}={\frac {1}{4\pi }}\left[\mathbf {E} \otimes \mathbf {E} +\mathbf {H} \otimes \mathbf {H} -{\frac {E^{2}+H^{2}}{2}}\mathbb {I} \right],}](/images/008/662/8662876/23.jpg?rand=150606)
где ⊗ —
диадическое произведение
, а последний тензор
 — единичная диада:
— единичная диада:
-

Элемент
ij
тензора напряжений Максвелла имеет единицы импульса на единицу площади в единицу времени и даёт поток импульса, параллельный
i
-й оси, пересекающий поверхность, перпендикулярную
j
-й оси (в отрицательном направлении) в единицу времени.
Эти единицы также можно рассматривать как единицы силы на единицу площади (отрицательное давление), а элемент
ij
тензора также можно интерпретировать как силу, параллельную оси
i
, действующую на поверхность, перпендикулярную оси j, на единицу. площади. Действительно, диагональные элементы задают натяжение (напряжение, вытягивание), действующее на дифференциальный элемент площади по нормали к соответствующей оси. В отличие от сил, вызванных давлением идеального газа, элемент площади в электромагнитном поле также испытывает силу, направленную не по нормали к элементу. Этот сдвиг задается недиагональными элементами тензора напряжений.
Только магнетизм
Если поле является только магнитным (что в значительной степени верно, например, для двигателей), некоторые члены выпадают, и уравнение в единицах СИ принимает вид:
-

Для цилиндрических объектов, таких как ротор двигателя, это выражение упрощается до:
-

где
r
— сдвиг в радиальном (наружу от цилиндра) направлении,
t
— сдвиг в тангенциальном (вокруг цилиндра) направлении. Это тангенциальная сила, которая вращает двигатель.
B
r
— плотность потока в радиальном направлении, а
B
t
— плотность потока в тангенциальном направлении.
В электростатике
В
электростатике
эффекты магнетизма отсутствуют. В этом случае магнитное поле исчезает,
 , и мы получаем
тензор электростатических напряжений Максвелла
. Он дается в виде компонентов
, и мы получаем
тензор электростатических напряжений Максвелла
. Он дается в виде компонентов
-

и в символической форме
-

где
 является подходящим тождественным тензором (обычно
является подходящим тождественным тензором (обычно
 ).
).
Собственное значение
Собственные значения тензора напряжений Максвелла определяются выражением:
-

Эти собственные значения получаются итеративным применением леммы об определителе матрицы в сочетании с формулой Шермана-Моррисона .
Отмечая, что матрица характеристического уравнения,
 может записываться как
может записываться как
-

где
-

мы устанавливаем
-

Применяя лемму об определителе матрицы один раз, мы получаем:
-

Применение его снова даёт,
-

Из последнего множимого из правой части выражения сразу видно, что
 является одним из собственных значений.
является одним из собственных значений.
Чтобы найти обратную
 , воспользуемся формулой Шермана-Моррисона:
, воспользуемся формулой Шермана-Моррисона:
-

Факторизовав
 членом определителя, нам осталось найти нули рациональной функции:
членом определителя, нам осталось найти нули рациональной функции:
-

Таким образом, как только мы решим
-

мы получаем два других собственных значения.
Смотрите также
Ссылки
-
Дэвид Дж. Гриффитс, «Введение в электродинамику», стр. 351–352, Benjamin Cummings Inc., 2008 г.
-
Джон Дэвид Джексон, «Классическая электродинамика, 3-е изд.», John Wiley & Sons, Inc., 1999.
-
Ричард Беккер, «Электромагнитные поля и взаимодействия», Dover Publications Inc., 1964.












![{\displaystyle \mathbf {f} =\varepsilon _{0}\left[({\boldsymbol {\nabla }}\cdot \mathbf {E} )\mathbf {E} -\mathbf {E} \times ({\boldsymbol {\nabla }}\times \mathbf {E} )\right]+{\frac {1}{\mu _{0}}}\left[-\mathbf {B} \times \left({\boldsymbol {\nabla }}\times \mathbf {B} \right)\right]-\varepsilon _{0}{\frac {\partial }{\partial t}}\left(\mathbf {E} \times \mathbf {B} \right).}](/images/008/662/8662876/12.jpg?rand=75182)
![{\displaystyle \mathbf {f} =\varepsilon _{0}\left[({\boldsymbol {\nabla }}\cdot \mathbf {E} )\mathbf {E} -\mathbf {E} \times ({\boldsymbol {\nabla }}\times \mathbf {E} )\right]+{\frac {1}{\mu _{0}}}\left[({\boldsymbol {\nabla }}\cdot \mathbf {B} )\mathbf {B} -\mathbf {B} \times \left({\boldsymbol {\nabla }}\times \mathbf {B} \right)\right]-\varepsilon _{0}{\frac {\partial }{\partial t}}\left(\mathbf {E} \times \mathbf {B} \right).}](/images/008/662/8662876/13.jpg?rand=922566)

![{\displaystyle \mathbf {f} =\varepsilon _{0}\left[({\boldsymbol {\nabla }}\cdot \mathbf {E} )\mathbf {E} +(\mathbf {E} \cdot {\boldsymbol {\nabla }})\mathbf {E} \right]+{\frac {1}{\mu _{0}}}\left[({\boldsymbol {\nabla }}\cdot \mathbf {B} )\mathbf {B} +(\mathbf {B} \cdot {\boldsymbol {\nabla }})\mathbf {B} \right]-{\frac {1}{2}}{\boldsymbol {\nabla }}\left(\varepsilon _{0}E^{2}+{\frac {1}{\mu _{0}}}B^{2}\right)-\varepsilon _{0}{\frac {\partial }{\partial t}}\left(\mathbf {E} \times \mathbf {B} \right).}](/images/008/662/8662876/15.jpg?rand=130235)







![{\displaystyle {\overset {\leftrightarrow }{\boldsymbol {\sigma }}}={\frac {1}{4\pi }}\left[\mathbf {E} \otimes \mathbf {E} +\mathbf {H} \otimes \mathbf {H} -{\frac {E^{2}+H^{2}}{2}}\mathbb {I} \right],}](/images/008/662/8662876/23.jpg?rand=150606)