Горизонтальная система координат ^:40 , или горизонтная система координат ^:30 — это система небесных координат , в которой основной плоскостью является плоскость математического горизонта , а полюсами — зенит и надир . Она применяется при наблюдениях звёзд и движения небесных тел Солнечной системы на местности невооружённым глазом, в бинокль или телескоп с азимутальной установкой ^:85 . Горизонтальные координаты не только планет и Солнца, но и звёзд непрерывно изменяются в течение суток ввиду суточного вращения небесной сферы .

Описание

Линии и плоскости

Горизонтальная система координат всегда топоцентрическая. Наблюдатель всегда находится в фиксированной точке на поверхности земли (отмечена буквой O на рисунке). Будем предполагать, что наблюдатель находится в Северном полушарии Земли на широте φ. При помощи отвеса определяется направление на зенит (z), как верхняя точка, в которую направлен отвес, а надир (Z') — как нижняя (под Землёй) ^:38 . Поэтому и линия (ZZ'), соединяющая зенит и надир называется отвесной линией ^:12 .

Плоскость, перпендикулярная к отвесной линии в точке O называется плоскостью математического горизонта . На этой плоскости определяется направление на юг (географический, не магнитный!) и север, например, по направлению кратчайшей за день тени от гномона . Кратчайшей она будет в истинный полдень , и линия (NS), соединяющая юг с севером, называется полуденной линией ^:39 . Точки востока (E) и запада (W) берутся отстоящими на 90 градусов от точки юга соответственно против и по ходу часовой стрелки, если смотреть из зенита. Таким образом, NESW — плоскость математического горизонта.

Плоскость, проходящая через полуденную и отвесную линии (ZNZ'S) называется плоскостью небесного меридиана , а плоскость, проходящая через небесное тело — плоскостью вертикала данного небесного тела. Большой круг, по которому она пересекает небесную сферу, называется вертикалом небесного тела ^:40 .

Координаты

В горизонтальной системе координат одной координатой является либо высота светила h , либо его зенитное расстояние z . Другой координатой является азимут A .

Высотой h светила называется дуга вертикала светила от плоскости математического горизонта до направления на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру ^:40 .

Зенитным расстоянием z светила называется дуга вертикала светила от зенита до светила. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.

Азимутом A светила называется дуга математического горизонта от точки юга до вертикала светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360° ^:41 . Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии и навигации азимуты отсчитываются от точки севера .)

Особенности изменения координат небесных тел

За сутки звезда (а также в первом приближении — тело Солнечной системы) описывает круг, перпендикулярный оси мира (PP'), которая на широте φ наклонена к математическому горизонту на угол φ. Поэтому она будет двигаться параллельно математическому горизонту лишь при φ равном 90 градусов, то есть на Северном полюсе . Поэтому все звёзды, видимые там, будут незаходящими (в том числе и Солнце на протяжении полугода, см. долгота дня ) а их высота h будет постоянной. На других широтах доступные для наблюдений в данное время года звёзды делятся на

• заходящие и восходящие ^:16 (h в течение суток проходит через 0)
• незаходящие ^:16 (h всегда больше 0)
• невосходящие ^:16 (h всегда меньше 0)

Максимальная высота h звезды будет наблюдаться раз в день при одном из двух её прохождений через небесный меридиан — верхней кульминации , а минимальная — при втором из них — нижней кульминации. От нижней до верхней кульминации высота h звезды увеличивается, от верхней до нижней — уменьшается.

Переход к первой экваториальной

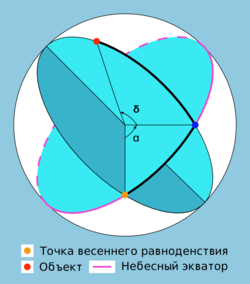
В дополнение к плоскости горизонта NESW, отвесной линии ZZ' и оси мира PP' начертим небесный экватор, перпендикулярный к PP' в точке O. Обозначим t — часовой угол светила, δ — его склонение, R — само светило, z — его зенитное расстояние. Тогда горизонтальную и первую экваториальную систему координат свяжет сферический треугольник PZR, называемый первым астрономическим треугольником ^:68 , или параллактическим треугольником ^:36 . Формулы перехода от горизонтальной системы координат к первой экваториальной системе координат имеют следующий вид ^:18 :

${\displaystyle \sin(\delta )=\sin(\varphi )\cdot \cos(z)-\cos(\varphi )\cdot \sin(z)\cdot \cos(A)}$

${\displaystyle \cos(\delta )\cdot \sin(t)=\sin(z)\cdot \sin(A)}$

${\displaystyle \cos(\delta )\cdot \cos(t)=\cos(\varphi )\cdot \cos(z)+\sin(\varphi )\cdot \sin(z)\cos(A)}$

Вывод формул перехода

Последовательность применения формул сферической тригонометрии к сферическому треугольнику PZR такая же, как при выводе подобных формул для эклиптической системы координат : теорема косинусов, теорема синусов и формула пяти элементов ^:37 . По теореме косинусов имеем:

${\displaystyle \cos(90^{\circ }-\delta )=\cos(z)\cdot \cos(90^{\circ }-\varphi )+\sin(z)\cdot \sin(90^{\circ }-\varphi )\cdot \cos(180^{\circ }-A)}$

${\displaystyle \sin(\delta )=\sin(\varphi )\cdot \cos(z)-\cos(\varphi )\cdot \sin(z)\cdot \cos(A)}$

Первая формула получена. Теперь к тому же сферическому треугольнику применяем теорему синусов :

${\displaystyle {\frac {\sin(z)}{\sin(t)}}={\frac {\sin(90^{\circ }-\delta )}{\sin(180^{\circ }-A)}}}$

${\displaystyle \cos(\delta )\cdot \sin(t)=\sin(z)\cdot \sin(A)}$

Вторая формула получена. Теперь применяем к нашему сферическому треугольнику формулу пяти элементов :

${\displaystyle \sin(90^{\circ }-\delta )\cdot \cos(t)=\cos(z)\cdot \sin(90^{\circ }-\varphi )-\sin(z)\cdot \cos(90^{\circ }-\varphi )\cdot \cos(180^{\circ }-A)}$

${\displaystyle \cos(\delta )\cdot \cos(t)=\cos(\varphi )\cdot \cos(z)+\sin(\varphi )\cdot \sin(z)\cdot \cos(A)}$

Третья формула получена. Итак, все три формулы получены из рассмотрения одного сферического треугольника.

Переход от первой экваториальной

Формулы перехода от первой экваториальной системы координат к горизонтальной системе координат выводятся при рассмотрении того же сферического треугольника, применяя к нему те же формулы сферической тригонометрии, что и при обратном переходе ^:37 . Они имеют следующий вид ^:17 :

${\displaystyle \cos(z)=\sin(\varphi )\cdot \sin(\delta )+\cos(\varphi )\cdot \cos(\delta )\cos(t)}$

${\displaystyle \sin(A)\cdot \sin(z)=\cos(\delta )\cdot \sin(t)}$

${\displaystyle \cos(A)\cdot \sin(z)=-\cos(\varphi )\cdot \sin(\delta )+\sin(\varphi )\cdot \cos(\delta )\cdot \cos(t)}$

Примечания

См. также

• Система небесных координат
• Сферическая система координат