Interested Article - DES

- 2020-12-11
- 1
DES ( англ. Data Encryption Standard ) — алгоритм для симметричного шифрования , разработанный фирмой IBM и утверждённый правительством США в 1977 году как официальный стандарт ( FIPS 46-3). Размер блока для DES равен 64 битам . В основе алгоритма лежит сеть Фейстеля с 16 циклами ( раундами ) и ключом , имеющим длину 56 бит . Алгоритм использует комбинацию нелинейных (S-блоки) и линейных (перестановки E, IP, IP-1) преобразований. Для DES рекомендовано несколько режимов:
- ECB ( англ. e lectronic c ode b ook ) — режим «электронной кодовой книги» (простая замена);
- CBC ( англ. c ipher b lock c haining ) — режим сцепления блоков;
- CFB ( англ. c ipher f eed b ack ) — режим обратной связи по шифротексту ;
- OFB ( англ. o utput f eed b ack ) — режим обратной связи по выходу;
- Counter Mode (CM) — режим счётчика.
Прямым развитием DES в настоящее время является алгоритм Triple DES (3DES). В 3DES шифрование/расшифровка выполняются путём троекратного выполнения алгоритма DES.
История
В 1972 году было проведено исследование потребности правительства США в компьютерной безопасности. Американское «национальное бюро стандартов» (НБС) (ныне известное, как NIST — «национальный институт стандартов и технологий») определило необходимость в общеправительственном стандарте шифрования некритичной информации.
НБС проконсультировалось с АНБ (агентством национальной безопасности США) и 15 мая 1973 года объявило первый конкурс на создание шифра. Были сформулированы строгие требования к новому шифру. Фирма IBM представила на конкурсе разработанный ею шифр, называемый «Люцифер» ( Lucifer ). Шифры ни одного из конкурсантов (включая «Люцифер») не обеспечивали выполнение всех требований. В течение 1973—1974 годов IBM доработала свой «Люцифер»: использовала в его основе алгоритм Хорста Фейстеля , созданный ранее. 27 августа 1974 года начался второй конкурс. На сей раз шифр «Люцифер» сочли приемлемым.
17 марта 1975 года предложенный алгоритм DES был издан в «Федеральном реестре». В 1976 году для обсуждения DES было проведено два открытых симпозиума. На симпозиумах жёсткой критике подверглись изменения, внесённые в алгоритм организацией АНБ. АНБ уменьшило первоначальную длину ключа и S-блоки (блоки подстановки), критерии проектирования которых не раскрывались. АНБ подозревалось в сознательном ослаблении алгоритма с той целью, чтобы АНБ могло легко просматривать зашифрованные сообщения. Сенат США проверил действия АНБ и в 1978 году опубликовал заявление, в котором сообщалось следующее:
- в процессе разработки алгоритма представители АНБ убедили создателей DES в том, что уменьшенной длины ключа более чем достаточно для всех коммерческих приложений;
- представители АНБ косвенно помогали в разработке S-перестановок;
- окончательная версия алгоритма была, по мнению проверяющих, лучшим алгоритмом шифрования, к тому же лишённым статистической или математической слабости;
- представители АНБ никогда не вмешивались в разработку алгоритма DES.
В 1990 году Эли Бихам (Eli Biham) и Ади Шамир (Adi Shamir) провели независимые исследования по дифференциальному криптоанализу — основному методу взлома блочных алгоритмов симметричного шифрования . Эти исследования сняли часть подозрений в скрытой слабости S-перестановок. S-блоки алгоритма DES оказались намного более устойчивыми к атакам, чем если бы их выбрали случайно. Это означает, что такая техника анализа была известна АНБ ещё в 1970-х годах.
Алгоритм DES удалось «взломать» за 39 дней с помощью огромной сети, состоящей из десятков тысяч компьютеров .
Общественная организация « EFF », занимающаяся проблемами информационной безопасности и личной тайны в сети Интернет , инициировала исследование «DES Challenge II» с целью выявления проблем DES. В рамках исследования сотрудники фирмы «RSA Laboratory» построили суперкомпьютер стоимостью 250 тыс. долл. В 1998 году суперкомпьютер выполнил расшифровку данных, закодированных методом DES с использованием 56-битного ключа, менее чем за три дня. Суперкомпьютер получил название «EFF DES Cracker». Специально по этому случаю учёные организовали пресс-конференцию и с беспокойством говорили о том, что злоумышленники вряд ли упустят случай воспользоваться подобной уязвимостью.
Некоторые правительственные чиновники и специалисты утверждали, что для взлома кода DES требуется суперкомпьютер стоимостью в несколько миллионов долларов. «Правительству пора признать ненадёжность DES и поддержать создание более мощного стандарта шифрования», — сказал президент EFF Барри Штайнхардт. Экспортные ограничения, накладываемые правительством США, касаются технологий шифрования по ключам длиной более 40 бит. Однако, как показали результаты эксперимента RSA Laboratory, существует возможность взлома и более мощного кода. Проблема усугублялась тем, что стоимость постройки подобного суперкомпьютера неуклонно снижалась. «Через четыре-пять лет такие компьютеры будут стоять в любой школе», — заявил Джон Гилмор, руководитель проекта «DES Challenge» и один из основателей EFF.
DES является блочным шифром. Чтобы понять, как работает DES, необходимо рассмотреть принцип работы блочного шифра , сеть Фейстеля .
Блочный шифр


Входными данными для блочного шифра служат:
- блок размером n бит;
- ключ размером k бит.
На выходе (после применения шифрующих преобразований) получается зашифрованный блок размером n бит, причём незначительные различия входных данных, как правило, приводят к существенному изменению результата.
Блочные шифры реализуются путём многократного применения к блокам исходного текста некоторых базовых преобразований.
Базовые преобразования:
- сложное преобразование на одной локальной части блока;
- простое преобразование между частями блока.
Так как преобразования производятся поблочно, требуется разделение исходных данных на блоки необходимого размера. При этом формат исходных данных не имеет значения (будь то текстовые документы, изображения или другие файлы). Данные должны интерпретироваться в двоичном виде (как последовательность нулей и единиц) и только после этого должны разбиваться на блоки. Все вышеперечисленное может осуществляться как программными, так и аппаратными средствами.
Преобразования сетью Фейстеля
Это преобразование над векторами ( блоками ), представляющими собой левую и правую половины регистра сдвига. В алгоритме DES используются прямое преобразование сетью Фейстеля в шифровании (см. Рис.1) и обратное преобразование сетью Фейстеля в расшифровании (см. Рис.2).
Схема шифрования алгоритма DES


Схема шифрования алгоритма DES указана на Рис.3.
Исходный текст — блок 64 бит.
Процесс шифрования состоит из начальной перестановки, 16 циклов шифрования и конечной перестановки.
Начальная перестановка
Исходный текст (блок 64 бит) преобразуется c помощью начальной перестановки которая определяется таблицей 1:
| 58 | 50 | 42 | 34 | 26 | 18 | 10 | 2 | 60 | 52 | 44 | 36 | 28 | 20 | 12 | 4 |
| 62 | 54 | 46 | 38 | 30 | 22 | 14 | 6 | 64 | 56 | 48 | 40 | 32 | 24 | 16 | 8 |
| 57 | 49 | 41 | 33 | 25 | 17 | 9 | 1 | 59 | 51 | 43 | 35 | 27 | 19 | 11 | 3 |
| 61 | 53 | 45 | 37 | 29 | 21 | 13 | 5 | 63 | 55 | 47 | 39 | 31 | 23 | 15 | 7 |
По таблице первые 3 бита результирующего блока после начальной перестановки являются битами 58, 50, 42 входного блока , а его 3 последние бита являются битами 23, 15, 7 входного блока.
Циклы шифрования
Полученный после начальной перестановки 64-битовый блок IP(T) участвует в 16 циклах преобразования Фейстеля.
— 16 циклов преобразования Фейстеля :
Разбить IP(T) на две части , где — соответственно 32 старших битов и 32 младших битов блока IP(T)=
Пусть результат (i-1) итерации, тогда результат i-ой итерации определяется:
Левая половина равна правой половине предыдущего вектора . А правая половина — это битовое сложение и по модулю 2.
В 16-циклах преобразования Фейстеля функция f играет роль шифрования . Рассмотрим подробно функцию f.
Основная функция шифрования (функция Фейстеля)
Аргументами функции являются 32-битовый вектор и 48-битовый ключ , который является результатом преобразования 56-битового исходного ключа шифра . Для вычисления функции последовательно используются
- функция расширения ,
- сложение по модулю 2 с ключом
- преобразование , состоящее из 8 преобразований -блоков ,
- перестановка .
Функция расширяет 32-битовый вектор до 48-битового вектора путём дублирования некоторых битов из ; порядок битов вектора указан в таблице 2.
| 32 | 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 8 | 9 | 10 | 11 | 12 | 13 |
| 12 | 13 | 14 | 15 | 16 | 17 |
| 16 | 17 | 18 | 19 | 20 | 21 |
| 20 | 21 | 22 | 23 | 24 | 25 |
| 24 | 25 | 26 | 27 | 28 | 29 |
| 28 | 29 | 30 | 31 | 32 | 1 |
Первые три бита вектора являются битами 32, 1, 2 вектора . По таблице 2 видно, что биты 1, 4, 5, 8, 9, 12, 13, 16, 17, 20, 21, 24, 25, 28, 29, 32 дублируются. Последние 3 бита вектора — это биты 31, 32, 1 вектора . Полученный после перестановки блок складывается по модулю 2 с ключами и затем представляется в виде восьми последовательных блоков .
Каждый является 6-битовым блоком. Далее каждый из блоков трансформируется в 4-битовый блок с помощью преобразований . Преобразования определяются таблицей 3.

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 14 | 4 | 13 | 1 | 2 | 15 | 11 | 8 | 3 | 10 | 6 | 12 | 5 | 9 | 0 | 7 | |
| 1 | 0 | 15 | 7 | 4 | 14 | 2 | 13 | 1 | 10 | 6 | 12 | 11 | 9 | 5 | 3 | 8 | |
| 2 | 4 | 1 | 14 | 8 | 13 | 6 | 2 | 11 | 15 | 12 | 9 | 7 | 3 | 10 | 5 | 0 | |
| 3 | 15 | 12 | 8 | 2 | 4 | 9 | 1 | 7 | 5 | 11 | 3 | 14 | 10 | 0 | 6 | 13 | |
| 0 | 15 | 1 | 8 | 14 | 6 | 11 | 3 | 4 | 9 | 7 | 2 | 13 | 12 | 0 | 5 | 10 | |
| 1 | 3 | 13 | 4 | 7 | 15 | 2 | 8 | 14 | 12 | 0 | 1 | 10 | 6 | 9 | 11 | 5 | |
| 2 | 0 | 14 | 7 | 11 | 10 | 4 | 13 | 1 | 5 | 8 | 12 | 6 | 9 | 3 | 2 | 15 | |
| 3 | 13 | 8 | 10 | 1 | 3 | 15 | 4 | 2 | 11 | 6 | 7 | 12 | 0 | 5 | 14 | 9 | |
| 0 | 10 | 0 | 9 | 14 | 6 | 3 | 15 | 5 | 1 | 13 | 12 | 7 | 11 | 4 | 2 | 8 | |
| 1 | 13 | 7 | 0 | 9 | 3 | 4 | 6 | 10 | 2 | 8 | 5 | 14 | 12 | 11 | 15 | 1 | |
| 2 | 13 | 6 | 4 | 9 | 8 | 15 | 3 | 0 | 11 | 1 | 2 | 12 | 5 | 10 | 14 | 7 | |
| 3 | 1 | 10 | 13 | 0 | 6 | 9 | 8 | 7 | 4 | 15 | 14 | 3 | 11 | 5 | 2 | 12 | |
| 0 | 7 | 13 | 14 | 3 | 0 | 6 | 9 | 10 | 1 | 2 | 8 | 5 | 11 | 12 | 4 | 15 | |
| 1 | 13 | 8 | 11 | 5 | 6 | 15 | 0 | 3 | 4 | 7 | 2 | 12 | 1 | 10 | 14 | 9 | |
| 2 | 10 | 6 | 9 | 0 | 12 | 11 | 7 | 13 | 15 | 1 | 3 | 14 | 5 | 2 | 8 | 4 | |
| 3 | 3 | 15 | 0 | 6 | 10 | 1 | 13 | 8 | 9 | 4 | 5 | 11 | 12 | 7 | 2 | 14 | |
| 0 | 2 | 12 | 4 | 1 | 7 | 10 | 11 | 6 | 8 | 5 | 3 | 15 | 13 | 0 | 14 | 9 | |
| 1 | 14 | 11 | 2 | 12 | 4 | 7 | 13 | 1 | 5 | 0 | 15 | 10 | 3 | 9 | 8 | 6 | |
| 2 | 4 | 2 | 1 | 11 | 10 | 13 | 7 | 8 | 15 | 9 | 12 | 5 | 6 | 3 | 0 | 14 | |
| 3 | 11 | 8 | 12 | 7 | 1 | 14 | 2 | 13 | 6 | 15 | 0 | 9 | 10 | 4 | 5 | 3 | |
| 0 | 12 | 1 | 10 | 15 | 9 | 2 | 6 | 8 | 0 | 13 | 3 | 4 | 14 | 7 | 5 | 11 | |
| 1 | 10 | 15 | 4 | 2 | 7 | 12 | 9 | 5 | 6 | 1 | 13 | 14 | 0 | 11 | 3 | 8 | |
| 2 | 9 | 14 | 15 | 5 | 2 | 8 | 12 | 3 | 7 | 0 | 4 | 10 | 1 | 13 | 11 | 6 | |
| 3 | 4 | 3 | 2 | 12 | 9 | 5 | 15 | 10 | 11 | 14 | 1 | 7 | 6 | 0 | 8 | 13 | |
| 0 | 4 | 11 | 2 | 14 | 15 | 0 | 8 | 13 | 3 | 12 | 9 | 7 | 5 | 10 | 6 | 1 | |
| 1 | 13 | 0 | 11 | 7 | 4 | 9 | 1 | 10 | 14 | 3 | 5 | 12 | 2 | 15 | 8 | 6 | |
| 2 | 1 | 4 | 11 | 13 | 12 | 3 | 7 | 14 | 10 | 15 | 6 | 8 | 0 | 5 | 9 | 2 | |
| 3 | 6 | 11 | 13 | 8 | 1 | 4 | 10 | 7 | 9 | 5 | 0 | 15 | 14 | 2 | 3 | 12 | |
| 0 | 13 | 2 | 8 | 4 | 6 | 15 | 11 | 1 | 10 | 9 | 3 | 14 | 5 | 0 | 12 | 7 | |
| 1 | 1 | 15 | 13 | 8 | 10 | 3 | 7 | 4 | 12 | 5 | 6 | 11 | 0 | 14 | 9 | 2 | |
| 2 | 7 | 11 | 4 | 1 | 9 | 12 | 14 | 2 | 0 | 6 | 10 | 13 | 15 | 3 | 5 | 8 | |
| 3 | 2 | 1 | 14 | 7 | 4 | 10 | 8 | 13 | 15 | 12 | 9 | 0 | 3 | 5 | 6 | 11 |
Предположим, что , и мы хотим найти . Первый и последний разряды являются двоичной записью числа а, 0<=a<=3, средние 4 разряда представляют число b, 0<=b<=15. Строки таблицы S3 нумеруются от 0 до 3, столбцы таблицы S3 нумеруются от 0 до 15. Пара чисел (а, b) определяет число, находящееся в пересечении строки а и столбца b. Двоичное представление этого числа дает . В нашем случае , , а число, определяемое парой (3,7), равно 7. Его двоичное представление =0111. Значение функции (32 бит ) получается перестановкой Р, применяемой к 32-битовому блоку . Перестановка Р задана таблицей 4.
| 16 | 7 | 20 | 21 | 29 | 12 | 28 | 17 |
| 1 | 15 | 23 | 26 | 5 | 18 | 31 | 10 |
| 2 | 8 | 24 | 14 | 32 | 27 | 3 | 9 |
| 19 | 13 | 30 | 6 | 22 | 11 | 4 | 25 |
Согласно таблице 4, первые четыре бита результирующего вектора после действия функции f — это биты 16, 7, 20, 21 вектора
Генерирование ключей
Ключи получаются из начального ключа (56 бит = 7 байтов или 7 символов в ASCII ) следующим образом. Добавляются биты в позиции 8, 16, 24, 32, 40, 48, 56, 64 ключа таким образом, чтобы каждый байт содержал нечетное число единиц. Это используется для обнаружения ошибок при обмене и хранении ключей. Затем делают перестановку для расширенного ключа (кроме добавляемых битов 8, 16, 24, 32, 40, 48, 56, 64). Такая перестановка определена в таблице 5.

| 57 | 49 | 41 | 33 | 25 | 17 | 9 | 1 | 58 | 50 | 42 | 34 | 26 | 18 | |
| 10 | 2 | 59 | 51 | 43 | 35 | 27 | 19 | 11 | 3 | 60 | 52 | 44 | 36 | |
| 63 | 55 | 47 | 39 | 31 | 23 | 15 | 7 | 62 | 54 | 46 | 38 | 30 | 22 | |
| 14 | 6 | 61 | 53 | 45 | 37 | 29 | 21 | 13 | 5 | 28 | 20 | 12 | 4 |
Эта перестановка определяется двумя блоками и по 28 бит каждый. Первые 3 бита есть биты 57, 49, 41 расширенного ключа. А первые три бита есть биты 63, 55, 47 расширенного ключа. i=1,2,3…получаются из одним или двумя левыми циклическими сдвигами согласно таблице 6.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Число сдвига | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 |
Ключ , i=1,…16 состоит из 48 бит, выбранных из битов вектора (56 бит ) согласно таблице 7. Первый и второй биты есть биты 14, 17 вектора
| 14 | 17 | 11 | 24 | 1 | 5 | 3 | 28 | 15 | 6 | 21 | 10 | 23 | 19 | 12 | 4 |
| 26 | 8 | 16 | 7 | 27 | 20 | 13 | 2 | 41 | 52 | 31 | 37 | 47 | 55 | 30 | 40 |
| 51 | 45 | 33 | 48 | 44 | 49 | 39 | 56 | 34 | 53 | 46 | 42 | 50 | 36 | 29 | 32 |
Конечная перестановка
Конечная перестановка действует на (где ) и является обратной к первоначальной перестановке. Конечная перестановка определяется таблицей 8.
| 40 | 8 | 48 | 16 | 56 | 24 | 64 | 32 | 39 | 7 | 47 | 15 | 55 | 23 | 63 | 31 |
| 38 | 6 | 46 | 14 | 54 | 22 | 62 | 30 | 37 | 5 | 45 | 13 | 53 | 21 | 61 | 29 |
| 36 | 4 | 44 | 12 | 52 | 20 | 60 | 28 | 35 | 3 | 43 | 11 | 51 | 19 | 59 | 27 |
| 34 | 2 | 42 | 10 | 50 | 18 | 58 | 26 | 33 | 1 | 41 | 9 | 49 | 17 | 57 | 25 |
Схема расшифрования
При расшифровании данных все действия выполняются в обратном порядке. В 16 циклах расшифрования, в отличие от шифрования c помощью прямого преобразования сетью Фейстеля , здесь используется обратное преобразование сетью Фейстеля.
Схема расшифрования указана на Рис.6.
Ключ
, i=16,…,1, функция f, перестановка IP и
такие же, как и в процессе шифрования. Алгоритм генерации ключей зависит только от ключа пользователя, поэтому при расшифровании они идентичны.
Режимы использования DES
DES может использоваться в четырёх режимах.
-
Режим электронной кодовой книги
(
ECB
—
Electronic Codebook
): обычное использование DES как
блочного шифра
. Шифруемый текст разбивается на блоки, при этом каждый блок шифруется отдельно, не взаимодействуя с другими блоками (см. Рис.7).
-

Рис.7 Режим электронной кодовой книги — ECB
-
- Режим сцепления блоков шифротекста ( СВС — Cipher Block Chaining ) (см. Рис.8). Каждый очередной блок i>=1, перед зашифровыванием складывается по модулю 2 с предыдущим блоком зашифрованного текста . Вектор — начальный вектор, он меняется ежедневно и хранится в секрете.
-
Режим обратной связи по шифротексту
(
Cipher Feedback
) (см. Рис.9). В режиме
CFB
вырабатывается блочная «
»
. Начальный вектор
является синхропосылкой и предназначен для того, чтобы разные наборы данных шифровались по-разному с использованием одного и того же секретного ключа. Синхропосылка посылается получателю в открытом виде вместе с зашифрованным файлом. Алгоритм DES, в отличие от предыдущих режимов, используется только как шифрование (в обоих случаях).
-

Рис.9 Режим обратной связи по шифротексту — CFB
-
-
Режим обратной связи по выходу
(
OFB
—
Output Feedback
) (см. Рис.10). В режиме OFB вырабатывается блочная «гамма»
, i>=1. Режим также использует DES только как шифрование (в обоих случаях).
-

Рис.10 Режим обратной связи по выходу — OFB
-
Достоинства и недостатки режимов:
- В режимах ECB и OFB искажение при передаче одного 64-битового блока шифротекста приводит к искажению после расшифрования только соответствующего открытого блока , поэтому такие режимы используется для передачи по каналам связи с большим числом искажений.
Криптостойкость алгоритма DES
Нелинейность преобразований в DES средствами только S-блоков и использование слабых S-блоков позволяет осуществлять контроль над шифрованной перепиской. Выбор S-блоков требует соблюдения нескольких условий:
- Каждая строка каждого блока должна быть перестановкой множества {0, 1, 2, …, 15}
- S-блоки не должны являться линейной или афинной функцией своих аргументов.
- Изменение одного бита на входе S-блока должно приводить к изменению, по крайней мере, двух битов на выходе.
- Для каждого S-блока и любого аргумента х значение S ( x ) и должны различаться, по крайней мере, двумя битами.
Из-за небольшого числа возможных ключей (всего ), появляется возможность их полного перебора на быстродействующей вычислительной технике за реальное время. В 1998 году Electronic Frontier Foundation , используя специальный компьютер DES-Cracker, удалось взломать DES за 3 дня.
Слабые ключи
Слабыми ключами называется ключи k такие, что , где x — 64-битный блок.
Известны 4 слабых ключа, они приведены в таблице 9. Для каждого слабого ключа существует неподвижные точки , то есть таких 64-битных блоков х , для которых .
| Слабые ключи (hexadecimal) | ||
| 0101-0101-0101-0101 | ||
| FEFE-FEFE-FEFE-FEFE | ||
| 1F1F-1F1F-0E0E-0E0E | ||
| E0E0-E0E0-F1F1-F1F1 |
обозначает вектор, состоящий из 28 нулевых битов.
Частично слабые ключи
В алгоритме DES существуют слабые и частично слабые ключи. Частично слабые ключи — это такие пары ключей , что
Существуют 6 частично слабых пар ключей, они приведены в таблице 10. Для каждого из 12 частично слабых ключей существуют «антинеподвижные точки», то есть такие блоки х, что
| Пары частично слабых ключей | ||||
| 01FE-01FE-01FE-01FE,----FE01-FE01-FE01-FE01 | ||||
| 1FE0-1FE0-1FE0-1FE0,----E0F1-E0F1-E0F1-E0F1 | ||||
| 01E0-01E0-01F1-01F1,----E001-E001-F101-F101 | ||||
| 1FFE-1FFE-0EFE-0EFE,----FE1F-FE1F-FE0E-FE0E | ||||
| 011F-011F-010E-010E,----1F01-1F01-0E01-0E01 | ||||
| E0FE-E0FE-F1FE-F1FE,----FEE0-FEE0-FEF1-FEF1 |
Известные атаки на DES
| Методы атаки | Известные откр. тексты | Выбранные отк. тексты | Объём памяти | Количество операций |
| Полный поиск | qweqweqweqerqe | - | Незначительный | |
| Линейный Криптоанализ | - | Для текста | ||
| Линейный Криптоанализ | - | Для текста | ||
| Диффер. Криптоанализ | - | Для текста | ||
| Диффер. Криптоанализ | - | Для текста |
- Метод полного перебора требует одну известную пару шифрованного и расшифрованного текста, незначительный объём памяти, и его выполнение требует около шагов.
- Дифференциальный криптоанализ — первую такую атаку на DES заявили Бихам и Шамир . Эта атака требует шифрования открытых текстов, выбранных нападающим, и для её выполнения нужны примерно шагов. Теоретически являясь точкой разрыва, эта атака непрактична из-за чрезмерных требований к подбору данных и сложности организации атаки по выбранному открытому тексту. Сами авторы этой атаки Biham и Shamir заявили, что считают DES защищённым для такой атаки.
- Линейный криптоанализ разработан Matsui. Этот метод позволяет восстановить ключ DES с помощью анализа известных открытых текстов, при этом требуется примерно шагов для выполнения. Первый экспериментальный криптоанализ DES, основанный на открытии Matsui, был успешно выполнен в течение 50 дней на автоматизированных рабочих местах 12 HP 9735.
Для линейного и дифференциального криптоанализа требуется достаточно большой объём памяти для сохранения выбранных (известных) открытых текстов до начала атаки.
Увеличение криптостойкости DES
Чтобы увеличивать криптостойкость DES, появляются несколько вариантов: ( ), triple DES ( 3DES ), DESX , .
- Методы и 3DES основаны на DES, но увеличивают длину ключей (2DES — 112 бит, 3DES — 168 бит) и поэтому увеличивается криптостойкость .
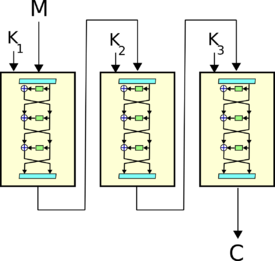
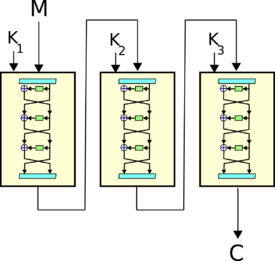
- Схема 3DES имеет вид , где ключи для каждого шифра DES. Это вариант известен как в ЕЕЕ, так как три DES операции являются шифрованием. Существует 3 типа алгоритма 3DES:
-
- : Шифруется три раза с 3 разными ключами.
- : 3DES операции шифровка-расшифровка-шифровка с 3 разными ключами.
- и : Как и предыдущие, за исключением того, что первая и третья операции используют одинаковый ключ.
- Самый популярный тип при использовании 3DES — это DES-EDE3, для него алгоритм выглядит так:
- Зашифрование : .
- Расшифрование :
-
При выполнении алгоритма 3DES ключи могут выбрать так:
- независимы.
- независимы, а
- .
- Метод DESX создан Рональдом Ривестом и формально продемонстрирована Killian и Rogaway. Этот метод — усиленный вариант DES, поддерживаемый инструментарием RSA Security. DESX отличается от DES тем, что каждый бит входного открытого текста DESX логически суммируется по модулю 2 с 64 битами дополнительного ключа, а затем шифруется по алгоритму DES. Каждый бит результата также логически суммируется по модулю 2 с другими 64 битами ключа. Главной причиной использования DESX является простой в вычислительном смысле способ значительно повысить стойкость DES к атакам полного перебора ключа.
- Метод разработан Schaumuller-Bichl для повышения производительности DES на основе увеличения размеров шифрованного блока. Заявлялось, что G-DES защищён так же, как и DES. Однако Biham и Shamir показали, что с рекомендуемыми параметрами легко взламывается, а при любых изменениях параметров шифр становится ещё менее защищён, чем DES.
- Ещё другой вариант DES использует независимые суб-ключи. Различно от алгоритма DES, в котором на основе 56-битного секретного ключа пользователя алгоритм DES получает шестнадцать 48-битных суб-ключей для использования в каждом из 16 раундов, в этом варианте использует 768-битный ключ (разделённый на 16 48-битных подключей) вместо 16 зависимых 48-битных ключей, создаваемых по ключевому графику алгоритма DES. Хотя очевидно, что использование независимых суб-ключей значительно усложнит полный поиск ключа, но стойкость к атаке дифференциальным или линейным криптоанализом ненамного превысит стойкость обычного DES. По оценке Biham для дифференциального криптоанализа DES с независимыми подключами требуется выбранных открытых текстов, в то время как для линейного криптоанализа требуется известных открытых текстов.
Применение
DES был национальным стандартом США в 1977 — 1980 гг., но в настоящее время DES используется (с ключом длины 56 бит) только для устаревших систем, чаще всего используют его более криптоустойчивый вид ( 3DES , DESX ). 3DES является простой эффективной заменой DES, и сейчас он рассмотрен как стандарт. В ближайшее время DES и Triple DES будут заменены алгоритмом AES (Advanced Encryption Standard — Расширенный Стандарт Шифрования). Алгоритм DES широко применяется для защиты финансовой информации: так, модуль THALES (Racal) HSM RG7000 полностью поддерживает операции TripleDES для эмиссии и обработки кредитных карт VISA , EuroPay и проч. Канальные шифраторы THALES (Racal) DataDryptor 2000 используют TripleDES для прозрачного шифрования потоков информации. Также алгоритм DES используется во многих других устройствах и решениях THALES-eSECURITY.
Примечания
- . Дата обращения: 1 января 2018. 31 декабря 2017 года.
Литература
- А. П. Алферов, А. Ю. Зубов, А. С. Кузьмин, А. В. Черемушкин . Основы криптографии.
- A. Menezes, Pvan Oorschot, S. Vanstone. .
- Семенов Ю. А. .
- 2020-12-11
- 1














































































































![{\displaystyle [0]^{28}}](/images/008/742/8742887/121.jpg?rand=101798)
![{\displaystyle [0]^{28}}](/images/008/742/8742887/122.jpg?rand=761188)
![{\displaystyle [1]^{28}}](/images/008/742/8742887/123.jpg?rand=543170)
![{\displaystyle [1]^{28}}](/images/008/742/8742887/124.jpg?rand=579010)
![{\displaystyle [0]^{28}}](/images/008/742/8742887/125.jpg?rand=94050)
![{\displaystyle [1]^{28}}](/images/008/742/8742887/126.jpg?rand=506436)
![{\displaystyle [1]^{28}}](/images/008/742/8742887/127.jpg?rand=470951)
![{\displaystyle [0]^{28}}](/images/008/742/8742887/128.jpg?rand=37205)
![{\displaystyle [0]^{28}}](/images/008/742/8742887/129.jpg?rand=579046)








![{\displaystyle [01]^{14}}](/images/008/742/8742887/138.jpg?rand=606417)
![{\displaystyle [01]^{14}}](/images/008/742/8742887/139.jpg?rand=525633)
![{\displaystyle [10]^{14}}](/images/008/742/8742887/140.jpg?rand=827540)
![{\displaystyle [10]^{14}}](/images/008/742/8742887/141.jpg?rand=389151)
![{\displaystyle [01]^{14}}](/images/008/742/8742887/142.jpg?rand=950002)
![{\displaystyle [01]^{14}}](/images/008/742/8742887/143.jpg?rand=297815)
![{\displaystyle [10]^{14}}](/images/008/742/8742887/144.jpg?rand=132977)
![{\displaystyle [10]^{14}}](/images/008/742/8742887/145.jpg?rand=711644)
![{\displaystyle [01]^{14}}](/images/008/742/8742887/146.jpg?rand=945515)
![{\displaystyle [0]^{28}}](/images/008/742/8742887/147.jpg?rand=821831)
![{\displaystyle [10]^{14}}](/images/008/742/8742887/148.jpg?rand=533606)
![{\displaystyle [0]^{28}}](/images/008/742/8742887/149.jpg?rand=635850)
![{\displaystyle [01]^{14}}](/images/008/742/8742887/150.jpg?rand=336289)
![{\displaystyle [1]^{28}}](/images/008/742/8742887/151.jpg?rand=830881)
![{\displaystyle [0]^{28}}](/images/008/742/8742887/152.jpg?rand=53067)
![{\displaystyle [1]^{28}}](/images/008/742/8742887/153.jpg?rand=265229)
![{\displaystyle [0]^{28}}](/images/008/742/8742887/154.jpg?rand=659415)
![{\displaystyle [01]^{14}}](/images/008/742/8742887/155.jpg?rand=606779)
![{\displaystyle [0]^{28}}](/images/008/742/8742887/156.jpg?rand=660368)
![{\displaystyle [10]^{14}}](/images/008/742/8742887/157.jpg?rand=134319)
![{\displaystyle [1]^{28}}](/images/008/742/8742887/158.jpg?rand=869248)
![{\displaystyle [01]^{14}}](/images/008/742/8742887/159.jpg?rand=361221)
![{\displaystyle [1]^{28}}](/images/008/742/8742887/160.jpg?rand=971626)
![{\displaystyle [10]^{14}}](/images/008/742/8742887/161.jpg?rand=695230)