Дедекиндово число — число ${\displaystyle M(n)}$ , равное количеству монотонных булевых функций от ${\displaystyle n}$ переменных. Эквивалентные определения: число антицепей подмножеств ${\displaystyle n}$ -элементного множества; число элементов в с ${\displaystyle n}$ производящими; число с ${\displaystyle n}$ элементами.

Последовательность ${\displaystyle (M(n))}$ — быстрорастущая, и хотя известны асимптотические оценки ${\displaystyle M(n)}$ и точное выражение в виде суммы , но явной вычислительной формулы нет, в связи с чем точное нахождение дедекиндовых чисел остаётся крайне сложной вычислительной задачей; по состоянию на 2023 год точные значения известны для ${\displaystyle n\leqslant 9}$ :

2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788, 286386577668298411128469151667598498812366.

Числа от ${\displaystyle M(0)}$ до ${\displaystyle M(4)}$ вычислил Дедекинд в 1897 году и сформулировал задачу Дедекинда — найти способ вычисления последующих чисел. Число ${\displaystyle M(5)}$ вычислил Чёрч в 1940 году , результат опроверг гипотезу Биркгофа , что ${\displaystyle M(n)}$ всегда делится на ${\displaystyle (2n-1)(2n-2)}$ . Числа ${\displaystyle M(6)}$ , ${\displaystyle M(7)}$ , ${\displaystyle M(8)}$ , ${\displaystyle M(9)}$ были вычислены соответственно в 1946 , 1965 , 1991 и 2023 годах.

Для нахождения ${\displaystyle M(8)}$ использовался суперкомпьютер . Число ${\displaystyle M(9)}$ было получено двумя независимыми группами математиков: из Германии применил техники анализа формальных понятий и для вычислительной процедуры использовал графический ускоритель (5311 машиночаса на ^* ); второй группе математиков из Бельгии потребовалось 47 тыс. машиночасов вычислений на ПЛИС 10 GX под управлением суперкомпьютера Noctua 2 , занявших около трёх месяцев . Обе группы получили одинаковый результат вычислений числа ${\displaystyle M(9)}$ , Якель опубликовал препринт на три дня раньше бельгийских коллег.

Если ${\displaystyle n}$ чётно, то ${\displaystyle M(n)}$ также должно быть чётным .

Точная формула для вычисления дедекиндовых чисел на основе логического определения антицепей была выведена в 1988 году :

${\displaystyle M(n)=\sum _{k=1}^{2^{2^{n}}}\prod _{j=1}^{2^{n}-1}\prod _{i=0}^{j-1}\left(1-b_{i}^{k}b_{j}^{k}\prod _{m=0}^{\log _{2}i}(1-b_{m}^{i}+b_{m}^{i}b_{m}^{j})\right)}$ ,

где ${\displaystyle b_{i}^{k}}$ является ${\displaystyle i}$ -м битом числа ${\displaystyle k}$ , который может быть записан с помощью округления вниз :

${\displaystyle b_{i}^{k}=\left\lfloor {\frac {k}{2^{i}}}\right\rfloor -2\left\lfloor {\frac {k}{2^{i+1}}}\right\rfloor }$ ,

однако она бесполезна для практического вычисления значений ${\displaystyle M(n)}$ для больших ${\displaystyle n}$ ввиду большого числа членов суммирования.

В 2014 году был найден ещё один вариант формулы, с помощью которой суммированием можно найти дедекиндовы числа:

${\displaystyle M(n+2)=\sum _{\alpha ,\beta \in M_{n}}\left(|[\bot ,\alpha ]|2^{C_{\alpha },\beta }|[\beta ,\top ]|\right)}$

Эта формула позволяет разложить решетку антицепей на подрешетки в пространствах меньшей размерности.

Логарифм дедекиндова числа можно оценить с помощью границ:

${\displaystyle {n \choose \lfloor n/2\rfloor }\leqslant \log _{2}M(n)\leqslant {n \choose \lfloor n/2\rfloor }\left(1+O\left({\frac {\log n}{n}}\right)\right)}$ ,

где неравенство слева подсчитывает число антицепей, в которых каждое множество имеет в точности ${\displaystyle \lfloor n/2\rfloor }$ элементов; правая часть неравенства установлена в 1975 году .

В 1981 году были даны более точные оценки :

${\displaystyle M(n)=(1+o(1))2^{n \choose \lfloor n/2\rfloor }\exp a(n)}$

для чётных ${\displaystyle n}$ и:

${\displaystyle M(n)=(1+o(1))2^{n \choose \lfloor n/2\rfloor +1}\exp(b(n)+c(n))}$

для нечётных ${\displaystyle n}$ , где

${\displaystyle a(n)={n \choose n/2-1}(2^{-n/2}+n^{2}2^{-n-5}-n2^{-n-4})}$ ,

${\displaystyle b(n)={n \choose (n-3)/2}(2^{-(n+3)/2}+n^{2}2^{-n-6}-n2^{-n-3})}$ ,

${\displaystyle c(n)={n \choose (n-1)/2}(2^{-(n+1)/2}+n^{2}2^{-n-4})}$ .

Основная идея этих оценок заключается в том, что в большинстве антицепей все множества имеют размеры, очень близкие к ${\displaystyle n/2}$ . Для ${\displaystyle n=2,4,6,8}$ формула даёт оценку, которая имеет ошибку в 9,8 %, 10,2 %, 4,1 % и −3,3 % соответственно .

Пример

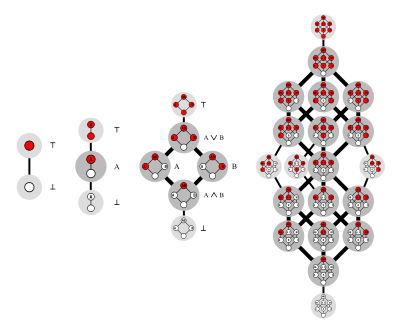
Для ${\displaystyle n=2}$ существует шесть монотонных булевых функций и шесть антицепей подмножеств двухэлементного множества ${\displaystyle \{x,y\}}$ :

• функция ${\displaystyle f(x,y)=\bot }$ , игнорирующая входные значения и всегда возвращающая ${\displaystyle \bot }$ , соответствует пустой антицепи ${\displaystyle \varnothing }$ ;
• логическая конъюнкция ${\displaystyle f(x,y)=x\wedge y}$ соответствует антицепи ${\displaystyle \{\{x,y\}\}}$ , содержащей единственное множество ${\displaystyle \{x,y\}}$ ;
• функция ${\displaystyle f(x,y)=x}$ , игнорирующая второй аргумент и возвращающая первый аргумент, соответствует антицепи ${\displaystyle \{\{x\}\}}$ , содержащей единственное множество ${\displaystyle \{x\}}$ ;
• функция ${\displaystyle f(x,y)=y}$ , игнорирующая первый аргумент и возвращающая второй аргумент, соответствует антицепи ${\displaystyle \{\{y\}\}}$ , содержащей единственное множество ${\displaystyle \{y\}}$ ;
• логическая дизъюнкция ${\displaystyle f(x,y)=x\vee y}$ соответствует антицепи ${\displaystyle \{\{x\},\{y\}\}}$ , содержащей два множества ${\displaystyle \{x\}}$ и ${\displaystyle \{y\}}$ ;
• функция ${\displaystyle f(x,y)=\top }$ , игнорирующая входные значения и всегда возвращающая истинное значение, соответствует антицепи ${\displaystyle \{\varnothing \}}$ , содержащей только пустое множество.

Примечания

Литература

• Joel Berman, Peter Köhler. Cardinalities of finite distributive lattices // Mitt. Math. Sem. Giessen. — 1976. — Т. 121 . — С. 103–124 .
• Randolph Church. // Duke Mathematical Journal. — 1940. — Т. 6 . — С. 732–734 . — doi : . .
• Randolph Church. Enumeration by rank of the free distributive lattice with 7 generators // Notices of the American Mathematical Society. — 1965. — Т. 11 . — С. 724 . . Как процитировано Видерманом ( harvtxt error: якоря не существует: CITEREFWiedemann1991 ( помощь ) ).
• Richard Dedekind . Über Zerlegungen von Zahlen durch ihre größten gemeinsamen Teiler // Gesammelte Werke. — 1897. — Т. 2. — С. 103–148.
• Jeff Kahn. Entropy, independent sets and antichains: a new approach to Dedekind's problem // Proceedings of the American Mathematical Society. — 2002. — Т. 130 , вып. 2 . — С. 371–378 . — doi : .
• Andrzej Kisielewicz. A solution of Dedekind's problem on the number of isotone Boolean functions // Journal für die Reine und Angewandte Mathematik. — 1988. — Т. 386 . — С. 139–144 . — doi : .
• Kleitman D., Markowsky G. On Dedekind's problem: the number of isotone Boolean functions. II // Transactions of the American Mathematical Society. — 1975. — Т. 213 . — С. 373–390 . — doi : . .
• Коршунов А. Д. О числе монотонных булевых функций // Проблемы кибернетики. — 1981. — Т. 38 . — С. 5–108 .
• Morgan Ward. Note on the order of free distributive lattices // Bulletin of the American Mathematical Society. — 1946. — Т. 52 . — С. 423 . — doi : .
• Doug Wiedemann. A computation of the eighth Dedekind number // . — 1991. — Т. 8 , вып. 1 . — С. 5–6 . — doi : . .
• Koichi Yamamoto. Note on the order of free distributive lattices // Science Reports of the Kanazawa University. — 1953. — Т. 2 , вып. 1 . — С. 5–6 .
• Nejib Zaguia. Isotone maps: enumeration and structure // Finite and Infinite Combinatorics in Sets and Logic (Proc. NATO Advanced Study Inst., Banff, Alberta, Canada, May 4, 1991) / Sauer N. W., Woodrow R. E., Sands B.. — Kluwer Academic Publishers, 1993. — С. 421–430.