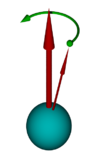
Прецессия линии узлов ( англ. Nodal precession ) — прецессия орбитальной плоскости спутника вокруг оси вращения астрономического объекта (например, Земли). Такой вид прецессии возникает из-за несферичности вращающегося тела, создающей неизотропное гравитационное поле. Следующие рассуждения относятся к спутникам на низкой околоземной орбите , не оказывающим заметного влияния на движение Земли. Прецессия линии узлов более массивных естественных спутников , например, Луны, более сложна.

Вокруг сферического тела орбитальная плоскость будет оставаться постоянной в пространстве под действием гравитации главного тела. Однако большинство тел вращается, что приводит к возникновению избытка массы на экваторе. Он создаёт гравитационное воздействие, приводящее к прецессии орбиты вокруг оси вращения главного тела.

Направление прецессии противоположно направлению вращения по орбите. При прямом движении вокруг Земли (в направлении вращения главного тела)долгота восходящего узла уменьшается, то есть прецессия происходит в западном направлении. Если орбита ретроградна, то долгота восходящего узла возрастает, то есть узел смещается в восточном направлении. Такая прецессия узлов позволяет поддерживать гелиосинхронные орбиты на почти постоянном угле относительно Солнца.

Описание

Невращающееся тело с размером порядка планеты или крупнее будет стремиться под действием гравитации приобрести шарообразную форму. В действительности все тела вращаются. Центробежная сила деформирует тело таким образом, что возникает утолщение на экваторе . Из-за наличия балджа результирующая сила притяжения спутника направлена не к центру главного тела, а немного смещена. В итоге тело притягивается в плоскость экватора, что создаёт момент, действующий на орбиту. Он не уменьшает наклонение, но создаёт гироскопическую прецессию, при которой со временем узлы орбиты смещаются.

Уравнение

Скорость прецессии зависит от наклонения орбитальной плоскости относительно плоскости экватора, а также от эксцентриситета орбиты.

Для спутника на орбите с прямым движением вокруг Земли прецессия происходит в западном направлении, то есть спутник и узлы орбиты движутся в противоположных направлениях. Хорошее приближение для темпа прецессии даёт следующая формула:

${\displaystyle \omega _{\mathrm {p} }=-{\frac {3}{2}}\cdot {\frac {{R_{\mathrm {E} }}^{2}}{\left(a\left(1-e^{2}\right)\right)^{2}}}J_{2}\omega \cos i,}$

где

ω _p — темп прецессии (в рад/с),

R _E — экваториальный радиус планеты ( 6 378 137 м для Земли),

a — большая полуось орбиты спутника,

e — эксцентриситет орбиты спутника,

ω — угловая скорость движения спутника (2π радианов, делённые на период, выраженный в секундах),

i — наклонение (в градусах),

J ₂ — второй динамический коэффициент формы ( − √ 5 C ₂₀ = 1,08262668⋅10 ⁻³ для Земли).

Последняя величина связана со сплюснутостью соотношением

${\displaystyle J_{2}={\frac {2\varepsilon _{\mathrm {E} }}{3}}-{\frac {{R_{\mathrm {E} }}^{3}{\omega _{\mathrm {E} }}^{2}}{3GM_{\mathrm {E} }}},}$

где

ε _E — сплюснутость центрального тела,

R _E — экваториальный радиус центрального тела ( 6 378 137 м для Земли),

ω _E — скорость вращения центрального тела ( 7,292115⋅10 ⁻⁵ рад/с для Земли)

GM _E — произведение универсальной гравитационной постоянной и массы центрального тела ( 3,986004418⋅10 ¹⁴ м ³ /с ² для Земли).

Прецессия линии узлов для спутников на низкой околоземной орбите обычно составляет несколько градусов в день в западном направлении. Если орбита круговая ( e = 0) и обладает высотой 800 км и наклонением 56° относительно экватора, то

${\displaystyle {\begin{aligned}R_{\mathrm {E} }&=6.378\,137\times 10^{6}{\text{м,}}\\J_{2}&=1.082\,626\,68\times 10^{-3}.\end{aligned}}}$

Орбитальный период равен 6052,4 с , поэтому угловая скорость равна 0,001038 рад/с . Прецессия имеет скорость

${\displaystyle {\begin{aligned}\omega _{\mathrm {p} }&=-{\frac {3}{2}}\cdot {\frac {6\,378\,137^{2}}{\left(7\,178\,137\left(1-0^{2}\right)\right)^{2}}}\cdot \left(1.082\,626\,68\times 10^{-3}\right)\cdot 0.001\,038\cdot \cos 56^{\circ }\\&=-7.44\times 10^{-7}{\text{ рад/с}}.\end{aligned}}}$

Эта величина эквивалентна −3,683° в день, поэтому плоскость орбиты совершит полный оборот (в инерциальной системе отсчёта) за 98 дней.

Видимое движение Солнца составляет около +1° в сутки (360° в год / 365,2422 суток в тропическом годе ≈ 0,9856473° в день), поэтому видимое движение Солнца относительно плоскости орбиты составит 2,8° в сутки, что даст полный цикл за 127 дней. Для ретроградных орбит ω отрицательно, поэтому прецессия становится положительной. (Иначе, ω можно считать положительной, но наклонением большим 90°, поэтому косинус наклонения отрицателен.) В таком случае возможно сделать так, чтобы прецессия соответствовала видимому движению Солнца, что используется в гелиосинхронных орбитах.

Примечания

Ссылки

• от 1 февраля 2020 на Wayback Machine
• 10 апреля 2013 года.