Interested Article - Тороидальный многогранник

с удалёнными ромбовидными гранями как тороидальный многогранник рода 11. Все грани этого многогранники являются правильными многоугольниками.

Можно построить многоугольный тор для приближения к поверхности тора развёрткой с четырёхугольными гранями, как показано на этом примере.

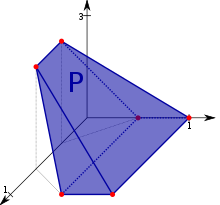
Тороидальный многогранник — это многогранник , который является также тороидом ( тор с g дырами), имеющий топологический род , g , равный 1 или выше.

Варианты определения

Тороидальные многогранники определяются как набор многоугольников , которые имеют общие вершины и рёбра, образуя многообразие . То есть, каждое ребро должно быть общим в точности для двух многоугольников, вершинная фигура каждой вершины должна быть одним циклом из многоугольников, которым данная вершина принадлежит. Для тороидальных многогранников это многообразие будет ориентированной поверхностью . Некоторые авторы ограничивают понятие «тороидальный многогранник» до многогранников, топологически эквивалентных (рода 1) тору .

Здесь следует различать вложенные тороидальные многогранники, грани которых являются плоскими не пересекающими друг друга многоугольниками в трёхмерном евклидовом пространстве , от , топологических поверхностей без определённой геометрической реализации . Серединой между этими двумя крайностями можно считать погружённые тороидальные многогранники, то есть многогранники, образованные многоугольниками или звёздчатыми многоугольниками в евклидовом пространстве, которым разрешено пересекать друг друга.

Во всех этих случаях тороидальная природа многогранников может быть проверена ориентированностью и эйлеровой характеристикой, которая для этих многогранников не положительна.

Многогранники Часара и Силаши

Многогранники Часара и Силаши

Многогранник Часара	Многогранник Силаши

Два самых простых возможных вложенных тороидальных многогранника — это многогранники Часара и Силаши.

Многогранник Часара — это тороидальный многогранник с семью вершинами, 21 ребром и 14 треугольными гранями . Только этот многогранник и тетраэдр (из известных) обладают свойством, что любой отрезок, соединяющий вершины многогранника является ребром многогранника . Двойственным многогранником является многогранник Силаши , который имеет 7 шестиугольных граней, каждая пара которых смежна друг другу , обеспечивая половину теоремы о том, что максимальное значение цветов для раскраски карты на торе (рода 1) равно семи .

Многогранник Часара имеет наименьшее возможное число вершин, которое может иметь вложенный тороидальный многогранник, а многогранник Силаши имеет наименьшее возможное число граней.

Тороиды Стюарта

Тороиды Стюарта

Шесть шестиугольных призм	Четыре квадратных купола 8 тетраэдров	Восемь октаэдров

Специальная категория тороидальных многогранников строится исключительно с помощью правильных многоугольных граней без их пересечения с дополнительным ограничением, что смежные грани не лежат в одной плоскости. Эти многогранники называются тороидами Стюарта по имени профессора , который исследовал их существование . Они аналогичны телам Джонсона в случае выпуклых многогранников , но, в отличие от них, существует бесконечно много тороидов Стюарта . Эти многогранники включают также торотоидальные дельтаэдры , многогранники, грани которых являются равносторонними треугольниками.

Ограниченный класс тороидов Стюарта, также определённых Стюартом, — это квазивыпуклые тороидальные многогранники . Это тороиды Стюарта, которые включают все рёбра их выпуклых оболочек . У этих многогранников каждая грань выпуклой оболочки либо лежит на поверхности тороида, либо является многоугольником, рёбра которого лежат на поверхности тороида .

Погружённые многогранники

		Большой додекаэдр

Многогранник, образованный системой пересекающихся многоугольников в пространстве — это многогранное погружение абстрактного топологического многообразия, образованного его многоугольниками и его системой рёбер и вершин. Примеры включают (род 1), (род 3) и большой додекаэдр (род 4).

Пятиугольный стефаноид. Этот стефаноид имеет пятиугольную диэдральную симметрию и имеет те же самые вершины, что и однородная пятиугольная призма .

Корончатый многогранник (или стефаноид ) — это тороидальный многогранник, который является многогранником, будучи как изогональным (одинаковые типы вершин), так и изоэдральным (одинаковые грани). Корончатый многогранник является самопересекающимся и топологически самодвойственным .

См. также

Примечания

; , стр. 15.
, с. 31—44.
, с. 46—58, 73.
, с. 140—142.
, с. 191—213.
, с. 69—80.
, с. 322—339.
, с. 231—268.
.
, с. 15.
, «Quasi-convexity and weak quasi-convexity», стр. 76—79.
, с. 43—70.

Литература

Branko Grünbaum. Polytopes: Abstract, Convex and Computational. — Kluwer Academic Publishers, 1994. — Т. 440. — (NATO ASI Series C: Mathematical and Physical Series). — doi : . . См., в частности, .
Robert Webb. // Symmetry: Culture and Science. — 2000. — Т. 11 , вып. 1—4 .
B. M. Stewart. Adventures Among the Toroids: A Study of Orientable Polyhedra with Regular Faces. — 2nd. — B. M. Stewart, 1980. — ISBN 978-0-686-11936-4 .
Lajos Szilassi. // Structural Topology. — 1986. — Т. 13 . (недоступная ссылка)
P. J. Heawood. Map colouring theorems // Quarterly J. Math. Oxford Ser.. — 1890. — Т. 24 .
A. Császár. A polyhedron without diagonals // Acta Sci. Math. Szeged. — 1949. — Т. 13 .
Günter M. Ziegler. Discrete Differential Geometry / A. I. Bobenko, P. Schröder, J. M. Sullivan, G. M. Ziegler. — Springer-Verlag, 2008. — Т. 38 . — ISBN 978-3-7643-8620-7 . — doi : . — arXiv : .
Walter Whiteley. // Structural Topology. — 1979. — Вып. 1 .
William T. Webber. Monohedral idemvalent polyhedra that are toroids // Geometriae Dedicata . — 1997. — Т. 67 , вып. 1 . — doi : .