Interested Article - Магниторотационная неустойчивость

- 2020-12-31
- 1
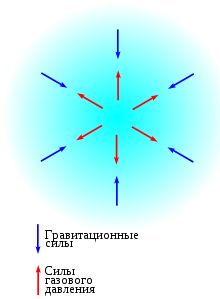
Магниторотационная неустойчивость (МРН) — неустойчивость проводящей жидкости, вращающейся в магнитном поле . Устойчивость вращающейся жидкости без магнитного поля изучалась Куэттом (Couette, 1890) , Маллоком (Mallock, 1896) , Рэлеем (Rayleigh, 1917) , Тейлором (Taylor, 1923) . Локальное условие устойчивости вращающейся жидкости можно получить из следующих соображений. Выберем произвольный элемент жидкости (элемент объёма) в слое, расположенном на некотором расстоянии от оси вращения, и сместим по радиусу этот элемент. В новом положении при малой вязкости (то есть при большом числе Рейнольдса ) элемент сохранит момент количества движения , пропорциональный его азимутальной скорости. Дальнейшее движение элемента по радиусу будет зависеть от соотношения между центробежной силой , действующей на него, и градиентом давления в этом слое. В равновесии градиент давления уравновешивает центробежную силу, действующую на окружающую жидкость. Если окружающая жидкость имеет меньший момент количества движения, то равновесный градиент давления окажется недостаточным для удержания в этом слое смещённого элемента и разовьётся неустойчивость. Таким образом, течение оказывается неустойчивым, если момент количества движения (на единицу массы) падает с радиусом ( )
Иное дело, если жидкость оказывается проводящей и помещена в магнитное поле. Для конкретности рассмотрим вращение хорошо проводящей жидкости (большое магнитное число Рейнольдса ) вокруг оси, параллельной магнитному полю. При смещении элемента объёма магнитная силовая линия оказывается вмороженной в исходный слой и сохраняется угловая скорость элемента. Для устойчивости течения необходимо, чтобы угловая скорость не падала с радиусом (Велихов, 1959) , то есть
Это условие глобально не может быть выполнено, так как скорость где-то превысит скорость света . При этом критерий не зависит от величины магнитного поля. Магнитное поле дестабилизирует течение вплоть до некого предельного значения. Сильное магнитное поле за счёт натяжения магнитных силовых линий стабилизирует поток.
В природе магниторотационная неустойчивость , по-видимому, наблюдается в жидком ядре Земли ( Велихов , 2005) , в звёздах , например в Солнце (Ruediger, 2004) , в аккреционных дисках (Balbus и Hawley, 1991) . В жидком ядре Земли источником неустойчивости может быть дифференциальное вращение , вызванное термической и химической конвекцией жидкого ядра. Дифференциальное вращение вызывает появление МРН , генерирующей магнитное поле. В свою очередь, поле ликвидирует дифференциальное вращение. В результате взаимодействие двух процессов, возможно, объясняет периодические срывы магнитного поля с характерным временем порядка 10000 лет, разделённые длительными периодами (сотни тысяч лет) стабильного существования поля. В Солнце МРН приводит к тому, что 70 процентов Солнца вращается как твёрдое тело (Ruediger) .
Проблема объяснения механизма падения вещества на притягивающий центр заключается в том, что при сохранении момента количества движения центробежная сила в аккреционном диске не позволит веществу упасть в центр. В 1973 году Н. И. Шакура и Р. А. Сюняев предложили модель сильно турбулентного аккреционного диска, вязкость в котором пропорциональна скорости звука и толщине диска . В 1991 году Бальбус (Balbus) и Хейли (Hawley) предположили, что магниторотационная неустойчивость вызывает эту турбулентность . МРН должна наблюдаться во вращающихся галактиках и других вращающихся объектах Вселенной. Если существует глобальное вращение Вселенной в целом, то оно должно приводить к появлению глобального магнитного поля.

Экспериментально магниторотационная неустойчивость изучается сейчас в ряде лабораторий: Университет Мэриленда (D. Lathrop, Maryland, USA), (Обнинск, Россия), Принстонский университет (Prinсеton, USA). Для наблюдения МРН необходимо достигнуть достаточно больших (существенно превосходящих единицу) магнитных чисел Рейнольдса, используя в качестве жидкости жидкий натрий. Самая крупная установка создана в Университете Мериленда (D. Lathrop, Maryland, USA) — вращающаяся сфера диаметром в 4 метра. Вторая проблема связана с созданием начального профиля скорости для изучения неустойчивости. Магнитное поле приводит к появлению вторичных течений, а высокие числа Рейнольдса приводят к возбуждению гидродинамической турбулентности. В ГНЦ РФ ФЭИ (Обнинск, Россия) вращение возбуждается током, протекающим поперёк магнитного поля, что может позволить исключить вторичные течения и гидродинамическую турбулентность . Можно надеяться на то, что в ближайшее время удастся экспериментально исследовать возникновение и развитие магнитогидродинамической турбулентности.
Ссылки
- M. Couette, Etudes sur le frottement des liquides , Annales de Chimie et de Physique. Vol. 6 (1890), 433—510.
- A. Mallock, Experiments on fluid viscosity , Philosophical Transactions of the Royal Society of London. Series A, 187 (1896), 41.
- L. Rayleigh, On the dynamics of revolving fluids , Proceedings of the Royal Society of London. Series A, Vol. 93, No. 648. (Mar. 1, 1917), 148—154.
- G. I. Taylor, Stability of a viscous liquid contained between two rotating cylinders , Philosophical Transactions of the Royal Society of London. Series A, 223 (1923), 289—343.
- Е. П. Велихов, Устойчивость течения идеально проводящей жидкости между вращающимися цилиндрами в магнитном поле , Журнал экспериментальной и теоретической физики (ЖЭТФ). Том 36 (1959), 1399.
- Е. П. Велихов, Магнитная геодинамика , Письма в ЖЭТФ. Том 82, вып. 11 (10 Дек. 2005), 785—790.
- ↑ G. Ruediger and R. Hollerbach, The Magnetic Universe . WILLEY-VCH, 2004.
- ↑ S.A. Balbus and J.F. Hawley, A Powerful Local Shear Instability in Weakly Magnetized Disks: I. Linear Analysis , Astrophysical Journal. Vol. 376 (1991), 214.
- N.I. Shakura and R.A. Sunyaev, Black holes in binary systems. Observational appearance , Astronomy and Astrophysics. Vol. 24 (1973), 337.
- 2020-12-31
- 1