Interested Article - Числа Люка

- 2021-04-04
- 1

Числа Люка задаются рекуррентной формулой
с начальными значениями и и с числами Фибоначчи . Эти числа названы в честь французского профессора Эдуарда Люка . Последовательность чисел Люка начинается так:
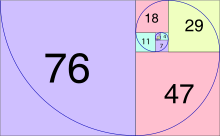
- 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, … (последовательность в OEIS )
Формула общего члена
Последовательность можно выразить как функцию от n :
где — золотое сечение . При n > 1 число |(− φ ) − n | меньше 0,5 и с ростом n всё сильнее приближается к нулю, а значит, при n > 1 числа Люка выражаются в виде где — функция округления к ближайшему целому .
Примечательно, что числа Фибоначчи выражаются похожим образом с помощью формулы Бине :
Проверка простоты числа с помощью чисел Люка
Числа Люка могут использоваться для проверки чисел на простоту . Чтобы проверить, является ли число p простым, возьмём ( p + 1)-ое число Люка, вычтем из него единицу — и если полученное число не делится на p нацело, то p гарантированно не является простым. В противном случае число может быть как простым, так и составным и требует более тщательной проверки.
В качестве примера проверим, является ли число 15 простым. 16-ое число Люка — 1364.
Следовательно, число 15 явно не простое.
Восемнадцатое число Люка равно 3571.
Значит, число 17 - простое.
Связь с числами Фибоначчи
Числа Люка связаны с числами Фибоначчи следующим формулами
- , и при стремлении к +∞ отношение стремится к
Обобщения
Числа Люка можно также определить для отрицательных индексов по формуле:
Эдуард Люка ввел понятие « обобщённых последовательностей Фибоначчи », частным случаем которых являются числа Фибоначчи и числа Люка
|
|
В статье
не хватает
ссылок на источники
(см.
рекомендации по поиску
).
|
- 2021-04-04
- 1









![{\displaystyle F_{n}={\frac {\varphi ^{n}-(1-\varphi )^{n}}{\sqrt {5}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\sqrt {5}}}={\frac {1}{\sqrt {5}}}\left[\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right].}](/images/009/109/9109083/11.jpg?rand=705558)