Interested Article - Уравнение состояния Ми — Грюнайзена

- 2021-06-05
- 2
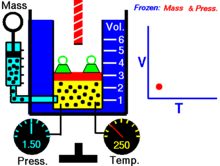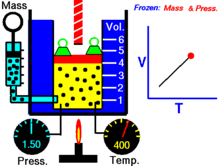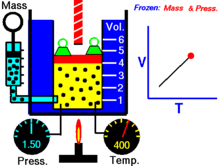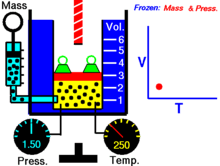
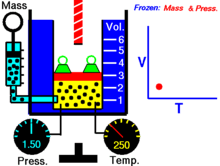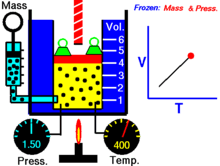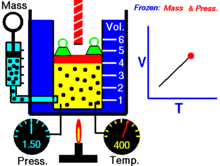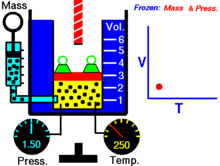
Уравнение состояния Ми — Грюнайзена — это уравнение, описывающее связь между давлением и объёмом тела при заданной температуре. Это уравнение в том числе используется для определения давления в процессе ударного сжатия твёрдого тела . Названо в честь немецкого физика . Уравнение состояния Ми — Грюнайзена представляется в следующей форме:
где p 0 и e 0 — давление и внутренняя энергия в начальном состоянии, V — объём, p — давление, e — внутренняя энергия, и Γ — коэффициент Грюнайзена, который характеризует термическое давление со стороны колеблющихся атомов. p — полное давление, p 0 — «холодное» давление. Коэффициент Грюнайзена безразмерен. В правой части уравнения Ми — Грюнайзена находится тепловое давление.
Функция Грюнайзена — мера изменения давления при изменении энергии системы при постоянном объёме. Она определяется по соотношению:
Производная берётся при постоянном объёме.
Уравнение Ми — Грюнайзена предполагает линейную зависимость давления от внутренней энергии. Для определения функции Грюнайзена используются методы статистической физики и предположение о линейности межатомных взаимодействий.
Оно используется для решения определённых термо-механических задач: определении эффектов ударной волны, термическом расширении твёрдых тел, быстром нагревании материалов из-за поглощения ядерного излучения .
Для вывода уравнения Ми — Грюнайзена используется уравнение Ранкина-Гюгонио для сохранения массы , момента и энергии:
где ρ 0 — относительная плотность , ρ — плотность после ударного сжатия, p H — давление Гюгонио, E H — удельная внутренняя энергия (на единицу массы) Гюгонио, U s — скорость удара, и U p — скорость частиц.
Параметры для различных материалов
Типичные различные для разных материалов величины для моделей в форме Ми — Грюнайзена.
| Материал | (kg/m 3 ) | (m/s) | (K) | ||||
|---|---|---|---|---|---|---|---|
| Медь | 8924 | 3910 | 1.51 | 1.96 | 1 | 0 | 0 |
| Вода | 1000 | 1483 | 2.0 | 2.0 | 10 −4 | 0 | 0 |
Параметр Грюнайзена для идеальных кристаллов с парными взаимодействиями
Выражение для параметра Грюнайзена для идеальных кристаллов с парными взаимодействиями в пространстве размерности имеет вид :
где — потенциал межатомного взаимодействия , — равновесное расстояние, — размерность пространства . Связь параметра Грюнайзена с параметрами потенциалов Леннард-Джонса, Ми и Морзе представлена в таблице.
| Решетка | Размерность | Потенциал Леннард-Джонса | Потенциал Морзе | |
|---|---|---|---|---|
| Цепочка | ||||
| Треугольная решётка | ||||
| ГЦК, ОЦК | ||||
| «Гиперрешётка» | ||||
| Общая формула |
Выражение для параметра Грюнайзена одномерной цепочки с взаимодействиями посредством потенциала Ми, приведенное в таблице, в точности совпадает с результатом статьи .
См. также
Литература
- ↑ Кривцов А. М., Кузькин В. А. Получение уравнений состояния идеальных кристаллов простой структуры // Известия РАН. Механика твёрдого тела. — 2011. — № 3. — С. 67—72.
- Vocadlo L., Poirer J.P., Price G.D. Grüneisen parameters and isothermal equations of state. American Mineralogist. — 2000. V. 85. — P. 390—395.
- Harris P., Avrami L. Some Physics of the Gruneisen Parameter. Technical report. — 1972.
- Shyue K.-M., A Fluid-Mixture Type Algorithm for Compressible Multicomponent Flow with Mie-Gruneisen Equation of State // Journal of Computational Physics. — 2001. Vol. 52. 3363 p.
- MacDonald, D. K. C.; Roy, S.K. (1955), "Vibrational Anharmonicity and Lattice Thermal Properties. II", Phys. Rev. , 97 : 673—676, doi :
- 2021-06-05
- 2











![{\displaystyle \Gamma _{0}=-{\frac {1}{2d}}{\frac {\Pi '''(a)a^{2}+(d-1)\left[\Pi ''(a)a-\Pi '(a)\right]}{\Pi ''(a)a+(d-1)\Pi '(a)}},}](/images/009/156/9156103/12.jpg?rand=279584)