Пафну́тий Льво́вич Чебышёв (ошибочн. Че́бышев ; 4 [16] мая 1821 , Окатово , Калужская губерния , Российская империя — 26 ноября [ 8 декабря ] 1894 , Санкт-Петербург , Российская империя ) — русский математик и механик , основоположник петербургской математической школы, академик Петербургской академии наук и ещё 24 академий мира .

Чебышёв — «величайший, наряду с Н. И. Лобачевским , русский математик XIX века» . Он получил фундаментальные результаты в теории чисел ( распределение простых чисел ) и теории вероятностей ( центральная предельная теорема , закон больших чисел ), построил общую теорию ортогональных многочленов , теорию равномерных приближений и многие другие. Основал математическую теорию синтеза механизмов и разработал ряд практически важных концепций механизмов.

Произношение и написание фамилии

Фамилию учёного — по его собственному указанию — следует произносить «Чебышо́в» ; в XIX веке такое произношение данной старинной дворянской фамилии (писавшейся тогда — в условиях традиционного неразличения е/ё на письме — как «Чебышевъ») было весьма распространено (предполагают, что эта фамилия по своему происхождению является кратким притяжательным прилагательным, образованным от антропонима Чебыш с ударением на окончании в косвенных падежах и на последнем слоге основы в именительном падеже ).

В XX веке в связи с тенденцией к обособлению фамилий на -ов/-ёв от исходных притяжательных прилагательных и всё ещё распространённым неразличением на письме е/ё получило довольно широкое распространение ошибочное произношение «Че́бышев» (с ударением на первом слоге) — несмотря на чёткие рекомендации авторитетных источников . 4-е издание академического «Русского орфографического словаря» (2013) , словарь ударений «Собственные имена в русском языке» (2001) и профильные академические издания , последовательно использующие букву ё при передаче имён и названий, фиксируют в качестве орфографической и орфоэпической нормы написание и произношение Чебышёв .

Биография

Пафнутий Чебышёв родился 4 ( 16 ) мая 1821 года в селе Окатово Боровского уезда Калужской губернии (ныне село Акатово Жуковского района Калужской области) в семье богатого землевладельца, представителя старинного русского дворянского рода Чебышёвых Льва Павловича Чебышёва — участника Отечественной войны 1812 года и взятия Парижа в 1814 году .

Дата рождения дана в соответствии с обнаруженной записью в метрической книге храма Преображения Господня в селе Спас-Прогнанье Калужской губернии (во многих источниках приводится дата 14 (26) мая , указанная К. А. Поссе в статье «Чебышёв, Пафнутий Львович» из энциклопедического словаря Брокгауза и Ефрона ). У Чебышёва были четыре брата и четыре сестры. Его младшие братья прославились как артиллеристы: один из них был начальником Кронштадтской крепостной артиллерии, другой — учёным, основоположником оружейного дела в России, заслуженным профессором Артиллерийской академии .

Первоначальное воспитание и образование получил дома: грамоте его обучила мать Аграфена Ивановна, арифметике и французскому языку — двоюродная сестра Авдотья Квинтилиановна Сухарёва. Кроме того, с детства Пафнутий занимался музыкой . Одним из детских увлечений будущего учёного было изучение механизмов игрушек и автоматов, причём он и сам придумывал и мастерил их. Этот интерес к механизмам сохранялся у Чебышёва и в зрелые годы .

В 1832 году семья переехала в Москву , чтобы продолжить образование взрослеющих детей. В Москве с Пафнутием математикой и физикой занимался П. Н. Погорельский — один из лучших учителей Москвы, у которого в том числе учился, в пансионе Вейденгаммера , и И. С. Тургенев . Латынь Пафнутию Чебышёву преподавал в то время студент-медик, а в будущем главный врач Шереметевской больницы А. Т. Тарасенков , за которого впоследствии вышла замуж сестра Пафнутия — Елизавета Чебышёва .

Летом 1837 года Чебышёв начал изучение математики в Московском университете на втором физико-математическом отделении философского факультета. Существенное влияние на формирование круга научных интересов молодого Чебышёва оказал его учитель — профессор прикладной математики и механики Московского университета Николай Дмитриевич Брашман ; благодаря ему, в частности, Чебышёв познакомился с работами французского инженера Жана-Виктора Понселе (известного, в частности, своими работами «Курс механики, применённой к машинам» (1826) и «Введение в индустриальную, физическую или экспериментальную механику» (1829)).

В 1840/1841 учебном году, участвуя в студенческом конкурсе, Чебышёв получил серебряную медаль за работу по нахождению корней уравнения n -й степени (сама работа была написана им ещё в 1838 году и сделана на основе алгоритма Ньютона ) .

В 1841 году Пафнутий Чебышёв окончил Императорский Московский университет. В это время дела его родителей из-за голода, охватившего в 1840 году значительную часть России, пришли в расстройство, и семья больше не могла материально поддерживать своего сына. Однако выпускник университета, невзирая на своё крайне стеснённое материальное положение, упорно продолжал заниматься наукой . В 1846 году он успешно защитил магистерскую диссертацию «Опыт элементарного анализа теории вероятностей» .

В 1847 году Чебышёв был утверждён в звании адъюнкт-профессора Петербургского университета . Чтобы получить право чтения лекций в университете, он защитил ещё одну диссертацию — на тему «Об интегрировании с помощью логарифмов», после чего читал лекции по высшей алгебре , теории чисел , геометрии , теории эллиптических функций и практической механике . Не раз он читал и курс теории вероятностей , изъяв из него расплывчатые формулировки и неправомерные утверждения и превратив его в строгую математическую дисциплину .

В 1849 году Чебышёв защитил в Петербургском университете докторскую диссертацию « Теория сравнений », после чего в 1850 году он стал профессором Петербургского университета; данную должность он занимал до 1882 года . Работая в Петербургском университете, Чебышёв близко сошёлся с профессором прикладной математики О. И. Сомовым , который тоже был учеником Н. Д. Брашмана , и эти отношения переросли в глубокую дружбу. В семейном плане Чебышёв был одинок, и это обстоятельство также способствовало его сближению с большой семьёй Сомова .

В 1852 году Чебышёв совершил научную командировку в Великобританию, Францию и Бельгию, в ходе которой он ознакомился с практикой зарубежного машиностроения, с музейными коллекциями машин и механизмов, с работой заводов и фабрик, а также встречался с крупнейшими математиками и механиками: О. Коши , Ж. Лиувиллем , Ж.-А. Серре , Л. Фуко , Ш. Эрмитом , Дж. Сильвестром , А. Кэли , Т. Грегори. После этого он некоторое время преподавал практическую механику в Петербургском университете и Александровском лицее .

В 1853 году академики П. Н. Фусс , В. Я. Струве , Б. С. Якоби , В. Я. Буняковский представили Чебышёва к избранию в адъюнкты Петербургской академии наук, особо отметив важность его работ в области практической механики. В том же году он был избран в адъюнкты, а в 1856 году стал экстраординарным академиком. В 1858 году в связи с его работами по теории шарнирных параллелограммов и теории приближения функций академики В. Я. Буняковский , М. В. Остроградский , Э. Х. Ленц , Б. С. Якоби , А. Я. Купфер , О. В. Струве подписали представление к избранию Чебышёва ординарным академиком, что и произошло в следующем году . Почётный член Московского университета (1858) . С 22 февраля 1860 года — ординарный профессор; с 10 июля 1863 года — член Учёного комитета Министерства народного просвещения ; с 30 августа 1863 года — действительный статский советник .

В 1863 году особая «Комиссия Чебышёва» принимала деятельное участие от Совета Санкт-Петербургского университета в разработке Университетского устава . Университетский устав, подписанный Александром II 18 июня 1863 года, предоставлял автономию университету как корпорации профессоров. Этот устав просуществовал до эпохи контрреформ правительства Александра III и рассматривался историками как наиболее либеральный и удачный университетский регламент в России XIX — начала XX веков .

П. Л. Чебышёв умер 26 ноября ( 8 декабря ) 1894 года за письменным столом . Погребён в родном имении, в селе Спас-Прогнанье (ныне Жуковского района Калужской области) в подклете храма Преображения Господня, рядом с могилами родителей .

Научная деятельность

Математика

Основные математические исследования П. Л. Чебышёва относятся к теории чисел , теории вероятностей , теории приближения функций , математическому анализу , геометрии , прикладной математике .

Творческий метод Чебышёва отличало стремление к увязке проблем математики с вопросами естествознания и техники и к соединению абстрактной теории с практикой . Учёный указывал: «Сближение теории с практикою даёт самые благотворные результаты, и не одна только практика от этого выигрывает: сами науки развиваются под влиянием её: она открывает им новые предметы для исследования или новые стороны в предметах давно известных… Если теория много выигрывает от новых приложений старой методы или от новых развитий её, то она ещё более приобретает открытием новых метод, и в этом случае науки находят себе верного руководителя в практике» .

Теория чисел

Из многочисленных открытий Чебышёва надо упомянуть прежде всего работы по теории чисел . Начало им было положено докторской диссертацией Чебышёва «Теория сравнений», напечатанной в 1849 году; она стала первой отечественной монографией по теории чисел. Этот труд несколько раз переиздавался, был переведён на немецкий и итальянский языки .

В 1851 году появился знаменитый его мемуар «Об определении числа простых чисел, не превосходящих данной величины» . К этому моменту была известна недоказанная гипотеза Лежандра , согласно которой функция распределения простых чисел ${\displaystyle \pi (x)}$ приближённо равна

${\displaystyle \pi (x)\approx {\frac {x}{\ln x-1{,}08366}}.}$

Чебышёв обнаружил гораздо лучшее приближение — интегральный логарифм (это предположение впервые высказал Гаусс в письме Энке (1849), однако не смог его обосновать):

${\displaystyle \pi (x)\approx \operatorname {li} x\equiv \int \limits _{2}^{x}{\frac {dt}{\ln t}}.}$

Чебышёв показал, что предел отношения ${\displaystyle \pi (x)/\operatorname {li} x}$ , если он существует, не может быть отличным от 1, и дал оценку возможным отклонениям ${\displaystyle \pi (x)}$ от интегрального логарифма. Он также показал, что если предел отношения ${\displaystyle \pi (x)/(x/\ln x)}$ существует, то он равен 1. Однако доказать существование этих пределов не смог. Позднее (в 1896 году) существование обоих пределов доказали — независимо друг от друга — Ж. Адамар и Ш. Ж. Валле-Пуссен .

Этот мемуар принёс 30-летнему Чебышёву общеевропейскую известность. В следующем, 1852 году Чебышёв опубликовал новую статью «О простых числах». В ней он провёл глубокий анализ сходимости рядов, зависящих от простых чисел, нашёл критерий их сходимости. В качестве приложения этих результатов он впервые доказал « постулат Бертрана » (выдвинутую Ж. Л. Бертраном гипотезу о том, что при ${\displaystyle n>3}$ между натуральными числами ${\displaystyle n}$ и ${\displaystyle 2n-2}$ находится по крайней мере одно простое число) и дал новую, весьма точную оценку для ${\displaystyle \pi (x)}$ :

${\displaystyle 0{,}92129<{\frac {\pi (x)}{x/\ln x}}<1{,}10555.}$

(данное неравенство позже сумели несколько усилить Дж. Сильвестр и И. Шур ) .

Чебышёв много занимался теорией квадратичных форм и связанными с ней проблемами делимости натуральных чисел и их разложения на простые множители . В своей статье 1866 года «Об одном арифметическом вопросе» он, используя аппарат непрерывных дробей , исследовал диофантовы приближения целых чисел . В аналитической теории чисел он одним из первых использовал гамма-функцию .

Теория вероятностей

Чебышёв стал первым русским математиком мирового уровня и в теории вероятностей . С 1860 года он сменил В. Я. Буняковского на кафедре теории вероятностей Петербургского университета и начал свой цикл лекций. Он опубликовал по данной теме всего четыре работы, но фундаментального характера. В статье «О средних величинах» (1866 год) было впервые доказано « неравенство Чебышёва », позднее усиленное Марковым :

${\displaystyle \mathbb {P} {\big (}{\big |}x-M[x]{\big |}\geqslant k\sigma {\big)}\leqslant {\frac {1}{k^{2}}}.}$

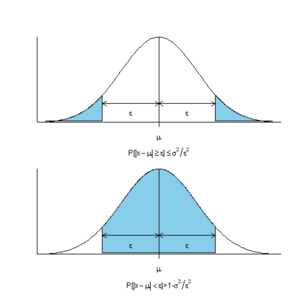
Эта формула означает, что вероятность отклонения любой случайной величины ${\displaystyle x}$ от её среднего значения ( математического ожидания ) ${\displaystyle M[x]}$ более чем на ${\displaystyle k}$ стандартных отклонений ( ${\displaystyle \sigma }$ ) не превышает ${\displaystyle 1/k^{2}}$ . Например, отклонение более чем на ${\displaystyle 5\sigma }$ имеет вероятность не более 1/25, то есть 4 %.

Хотя указанное неравенство впервые было опубликовано (без доказательства) И.-Ж. Бьенэме в 1853 году, за ним закрепилось название «неравенство Чебышёва» — в значительной мере потому, что П. Л. Чебышёв не только дал вывод этого неравенства, но и успешно применил его для решения важной проблемы — обоснования закона больших чисел .

Именно, в качестве следствия данного неравенства Чебышёв получил чрезвычайно общую формулировку закона больших чисел : если математические ожидания серии ${\displaystyle n}$ случайных величин и математические ожидания их квадратов ограничены в совокупности, то среднее арифметическое этих величин с ростом ${\displaystyle n}$ сходится к среднему арифметическому для их математических ожиданий. Из этой теоремы получаются как следствия теоремы Бернулли и Пуассона ; Чебышёв впервые строго оценил точность этих теорем и других приближений .

В этой же статье П. Л. Чебышёв впервые чётко обосновал общепринятую сегодня точку зрения на понятие случайной величины как на одно из основных понятий теории вероятностей .

В 1887 году появилась статья Чебышёва «О двух теоремах относительно вероятностей». В этой работе он установил, что при некоторых (достаточно общих) условиях выполняется центральная предельная теорема : сумма большого числа независимых случайных величин с нулевыми математическими ожиданиями (например, погрешностей измерения) распределена приближённо по нормальному закону, и тем точнее, чем больше слагаемых в сумме. Этот результат по своей общности далеко перекрывает теорему Муавра — Лапласа и все её аналоги . В ходе поисков доказательства теоремы Чебышёв разработал — для случая сходимости к нормальному распределению — метод, известный сейчас как метод моментов , то есть метод определения распределения вероятностей по его моментам .

Доказывая свой вариант центральной предельной теоремы, Чебышёв допустил логический пробел: оказалось, что — в дополнение к указанным Чебышёвым условиям применимости теоремы — следует ещё потребовать, чтобы среднее арифметическое дисперсий при стремлении ${\displaystyle n}$ к бесконечности имело предел. Данный недостаток был вскоре исправлен А. А. Марковым .

Обе упомянутые теоремы Чебышёва занимают центральное место в теории вероятностей. Особенно важно то обстоятельство, что Чебышёв не только указал предельное распределение, но в обоих случаях детально проанализировал границы возможных отклонений от этого предела . Исследования П. Л. Чебышёва продолжили его ученики, в первую очередь А. А. Марков и А. М. Ляпунов .

Теория приближения функций

Хотя теория приближения функций имеет достаточно богатую предысторию, собственно историю этого раздела математики принято исчислять с 1854 года, когда была опубликована статья П. Л. Чебышёва «Теория механизмов, известных под названием параллелограммов». Она стала первой из серии работ учёного по «функциям, наименее уклоняющимся от нуля» (исследованиям в данной области Чебышёв посвятил сорок лет) .

В упомянутой статье Чебышёв пришёл к выводу, что для приближения аналитической функции ${\displaystyle f}$ на некотором отрезке ${\displaystyle [a,b]}$ алгебраическим многочленом заданной степени формула Тейлора недостаточно эффективна, и поставил общую задачу о нахождении для заданной непрерывной функции многочлена наилучшего равномерного приближения . За меру уклонения функции ${\displaystyle f}$ от нуля он принял величину

${\displaystyle \max _{x\in [a,b]}|f(x)|;}$

сейчас её называют либо (следуя Чебышёву) уклонением от нуля , либо чебышёвской нормой функции ${\displaystyle f}$ . Фактически речь идёт о равномерной метрике в пространстве ${\displaystyle C[a,b]}$ непрерывных функций на отрезке ${\displaystyle X\equiv [a,b]}$ ; в этой метрике за меру различия между функциями ${\displaystyle f}$ и ${\displaystyle g}$ принимается величина

${\displaystyle d(f,g)=\max \limits _{X}|f(x)-g(x)|.}$

В соответствии с этим среди многочленов степени, не превышающей ${\displaystyle n}$ , многочленом наилучшего равномерного приближения для функции ${\displaystyle f}$ является такой многочлен ${\displaystyle U}$ , для которого чебышёвская норма разности ${\displaystyle f-U}$ минимальна .

Чебышёв установил характеристическое свойство такого многочлена: многочлен ${\displaystyle U}$ будет многочленом наилучшего равномерного приближения тогда и только тогда, когда на отрезке ${\displaystyle [a,b]}$ найдутся такие ${\displaystyle n+2}$ точки ${\displaystyle X_{i}}$ , что в них разность ${\displaystyle f-U}$ поочерёдно принимает свои максимальное и минимальное значения, равные по модулю ( точки чебышёвского альтернанса ). Позднее, в 1905 году, Э. Борель доказал существование и единственность многочлена наилучшего равномерного приближения . Начиная с середины XX века многочлены наилучшего приближения весьма часто используют в стандартных компьютерных программах для вычисления элементарных и специальных функций .

Аналогичный результат Чебышёв получил и для наилучшего равномерного приближения непрерывной функции рациональными дробями с фиксированными степенями числителя и знаменателя .

П. Л. Чебышёв поставил и решил задачу о нахождении многочленов, наименее уклоняющихся от нуля : на отрезке ${\displaystyle [-1,1]}$ это — такие многочлены степени ${\displaystyle n}$ с коэффициентом 1 при старшем члене, для которых уклонение от нуля на данном отрезке минимально. Оказалось, что решением данной задачи служат многочлены ${\displaystyle {\overline {T}}_{n}(x)=T_{n}(x)/2^{n-1}}$ с чебышёвской нормой, равной ${\displaystyle 1/2^{n-1}}$ (они лишь числовым множителем отличаются от многочленов Чебышёва 1-го рода). Многочлены, наименее уклоняющиеся от нуля на произвольном отрезке ${\displaystyle [a,b]}$ , получаются из рассмотренных линейной заменой независимой переменной .

Введённые П. Л. Чебышёвым многочлены, наименее уклоняющиеся от нуля, получили применение, в частности, в вычислительной линейной алгебре . Именно, начиная с 1950-х годов при решении систем линейных уравнений вида ${\displaystyle Ax=b}$ с симметричной положительно определённой матрицей ${\displaystyle A}$ получил распространение чебышёвский итерационный метод . Это — видоизменение метода простых итераций , в простейшем своём варианте имеющее вид

${\displaystyle x^{k+1}=x^{k}-\tau _{k}\,(Ax^{k}-b),\quad k=0,1,\dots }$

( ${\displaystyle x^{k}}$ — очередное приближение к точному решению системы), причём параметры ${\displaystyle \tau _{k}}$ подбираются из условия, что норма погрешности приближённого решения должна за очередной цикл из ${\displaystyle N}$ итераций ( ${\displaystyle N}$ задано заранее) уменьшаться максимально быстро. Оказалось, что если ${\displaystyle m}$ и ${\displaystyle M}$ — нижняя и верхняя границы для собственных значений матрицы ${\displaystyle A}$ , то на каждом цикле за ${\displaystyle \tau _{k}}$ следует брать числа, обратные значениям корней многочлена, наименее уклоняющегося от нуля на отрезке ${\displaystyle [m,M]}$ (при этом для обеспечения вычислительной устойчивости корни берут не подряд, а переупорядочивают специальным образом) . Наиболее важные приложения данный метод нашёл при численном решении эллиптических краевых задач .

Эта и последующие работы Чебышёва были весьма оригинальными — как по постановке задач, так и по предложенным методам их решения. Предложенная Чебышёвым постановка задачи о приближении функции существенно отличается от другого известного подхода, когда для оценки различия двух функций ${\displaystyle f}$ и ${\displaystyle g}$ часто используют какую-нибудь усреднённую характеристику разности этих функций — например, метрику L 2 {\displaystyle L_{2}} Лебега :

${\displaystyle d(f,g)={\sqrt {\int \limits _{X}(f(x)-g(x))^{2}\,\mu (dx)}}}$

(задача о наилучшем среднеквадратичном приближении ) .

Подход Чебышёва отличается тем, что в качестве критерия близости двух функций берётся не среднее, а максимальное их различие (чебышёвская норма разности функций). Этот подход предпочтителен во многих практических ситуациях — например, при работе механизма даже кратковременное существенное отклонение текущих параметров от стандартных может привести к снижению его работоспособности или даже разрушению . Аналогичные требования предъявляют картография (максимальное искажение масштаба на карте должно быть невелико), механика точных часовых механизмов и т. п .

Для картографии Чебышёв сформулировал в 1856 году теорему: «наивыгоднейшая конформная проекция для изображения какой-нибудь части земной поверхности на карте есть та, в которой на границе изображения масштаб сохраняет одну и ту же величину». Доказать её сумел 38 лет спустя ученик Чебышёва Д. А. Граве ; ныне данная теорема называется теоремой Чебышёва — Граве , а удовлетворяющие её условиям конформные проекции — чебышёвскими проекциями .

В начале XX века развитая в работах Чебышёва и его школы теория наилучшего приближения функций переросла в конструктивную теорию функций . При этом с появлением работ (1911) и С. Н. Бернштейна (1912) акценты сместились от задач индивидуального приближения функций к изучению поведения погрешностей приближения многочленами при стремлении ${\displaystyle n}$ к бесконечности .

П. Л. Чебышёв занимался также и классическим способом приближения функций — интерполированием . В 1859 году в работе «Вопросы о наименьших величинах, связанных с приближённым представлением функций» он показал, что погрешность интерполяции для функции, заданной на отрезке ${\displaystyle [-1,1]}$ , минимальна, если использовать корни многочленов Чебышёва 1-го рода ${\displaystyle T_{n}(x)}$ в качестве узлов интерполяции .

Математический анализ и геометрия

Проблемам интегрального исчисления Чебышёв посвятил мемуар 1860 года , в котором для заданного многочлена ${\displaystyle x^{4}+\alpha x^{3}+\beta x^{2}+\gamma x+\delta }$ с рациональными коэффициентами даётся алгоритм определения такого числа ${\displaystyle A}$ , что выражение ${\displaystyle {\frac {x+A}{\sqrt {x^{4}+\alpha x^{3}+\beta x^{2}+\gamma x+\delta }}}}$ интегрировалось в логарифмах , и вычисления соответствующего интеграла .

К работам последнего периода деятельности Чебышёва относятся исследования «О предельных значениях интегралов» («Sur les valeurs limites des intégrales», 1873). Совершенно новые вопросы, поставленные здесь учёным, разрабатывались затем его учениками. Последний мемуар Чебышёва 1895 года относится к той же области.

Чебышёву принадлежит теорема об условиях интегрируемости дифференциального бинома , опубликованная в мемуаре 1853 года «Об интегрировании иррациональных дифференциалов». Теорема устанавливает, что интеграл

${\displaystyle \int x^{m}(a+bx^{n})^{p}\,{\rm {d}}x\;}$ ,

где ${\displaystyle m}$ , ${\displaystyle n}$ , ${\displaystyle p}$ — рациональные числа, выражается в элементарных функциях только в трёх случаях (известных ещё в XVIII веке) :

• ${\displaystyle p}$ — целое число;
• ${\displaystyle {\frac {m+1}{n}}}$ — целое число;
• ${\displaystyle {\frac {m+1}{n}}\,+\,p}$ — целое число.

В 1882 году П. Л. Чебышёв доказал, что для заданных на отрезке ${\displaystyle [a,b]}$ монотонных функций ${\displaystyle f}$ и ${\displaystyle g}$ с неотрицательными значениями выполняется неравенство

${\displaystyle \int \limits _{a}^{b}f(x)\,{\rm {d}}x\,\int \limits _{a}^{b}g(x)\,{\rm {d}}x\,\;\leqslant \;\,(b-a)\,\int \limits _{a}^{b}f(x)\,g(x)\,{\rm {d}}x\;}$ ,

причём аналогичное неравенство

${\displaystyle \sum _{k=1}^{n}\,a_{k}\,\sum _{k=1}^{n}\,b_{k}\;\leqslant \;n\,\sum _{k=1}^{n}\,a_{k}\,b_{k}}$

справедливо и для конечных монотонных последовательностей неотрицательных чисел. Сейчас оба этих неравенства называют неравенствами Чебышёва .

Ряд важных результатов, полученных П. Л. Чебышёвым, относится к ещё одному разделу математического анализа — теории ортогональных многочленов ; получены они были в тесной связи с исследованиями по теории приближения функций. В 1854 году в работе «Теория механизмов, известных под названием параллелограммов» Чебышёв ввёл многочлены Чебышёва 1-го рода ${\displaystyle T_{n}(x)}$ и 2-го рода ${\displaystyle U_{n}(x)}$ и приступил к изучению их свойств (это были первые системы классических ортогональных многочленов , последовавшие за введёнными А. М. Лежандром ещё в 1785 году многочленами Лежандра ) .

В 1859 году в статье «О разложении функций одной переменной» Чебышёв ввёл две новые системы классических ортогональных многочленов. Ныне они известны как многочлены Чебышёва — Эрмита (или многочлены Эрмита ) и многочлены Чебышёва — Лагерра (или многочлены Лагерра ) ; названия связаны с тем, что позднее эти многочлены изучали соответственно Ш. Эрмит (1864) и Э. Лагерр (1878) . Все перечисленные системы ортогональных многочленов играют большую роль в математике, имея многообразные приложения. При этом Чебышёв на основе аппарата непрерывных дробей разработал общую теорию разложения произвольной функции в ряд по ортогональным многочленам .

Дифференциальной геометрии поверхностей была посвящена статья Чебышёва с необычным названием «О кройке одежды» (1878); в ней учёный ввёл новый класс координатных сеток, получивший название « сети Чебышёва » .

Прикладная математика

В течение сорока лет Чебышёв принимал активное участие в работе военного артиллерийского ведомства (с 1855 года — действительный член Артиллерийского отделения Военно-учёного комитета , с 1859 года — действительный член Временного артиллерийского комитета) и работал над усовершенствованием дальнобойности и точности артиллерийской стрельбы, применяя для обработки результатов опытных стрельб методы теории вероятностей. В курсах баллистики до наших дней сохранилась для вычисления дальности полёта снаряда в зависимости от его угла бросания, начальной скорости и сопротивления воздуха при заданной начальной скорости. Своими трудами Чебышёв оказал большое влияние на развитие русской артиллерийской науки, на приобщение учёных-артиллеристов к математике .

В тесной связи с работой Чебышёва во Временном артиллерийском комитете находились его исследования по квадратурным формулам . В ходе данных исследований он в 1873 году предложил новый тип квадратурных формул ( квадратурные формулы Чебышёва ). Эти формулы удовлетворяют дополнительному требованию равенства весов и позволяют упростить вычисления и сократить их объём, обладая следующим важным свойством: они доставляют минимум дисперсии вычисленного по ним приближённого значения интеграла (при условии, что погрешности в узлах независимы и имеют одинаковую дисперсию и равное нулю математическое ожидание) . Чебышёв нашёл явный вид данных формул для числа узлов ${\displaystyle n=2,\dots ,7}$ ; позднее С. Н. Бернштейн добавил к ним формулу с ${\displaystyle n=9}$ и доказал, что при ${\displaystyle n=8}$ и ${\displaystyle n\geqslant 10}$ таких формул не существует .

Механика

В области механики П. Л. Чебышёва интересовали вопросы прикладной механики и в особенности — теории механизмов ; последней посвящено около 15 работ учёного . Он не опубликовал ни одной работы по общим вопросам теоретической механики , однако в ряде работ его учеников ( П. И. Сомов , А. М. Ляпунов , Д. А. Граве ), относившихся к области теоретической механики, нашли своё отражение идеи, подсказанные их учителем. Фактически П. Л. Чебышёв возглавил после смерти М. В. Остроградского петербургскую ветвь самобытной русской школы механики .

Что касается теории механизмов, то историки науки выделяют три сложившиеся в России во 2-й половине XIX века научные школы в этой области: П. Л. Чебышёва в Петербурге (оформившаяся ранее двух остальных), В. Н. Лигина в Одессе и Н. Е. Жуковского в Москве. Под влиянием бесед с Чебышёвым задачами кинематики механизмов заинтересовались английские математики Дж. Сильвестр и А. Кэли .

Синтез механизмов

В 1850-е годы Чебышёв заинтересовался шарнирно-рычажными механизмами, служащими для приближённого преобразования кругового движения в прямолинейное и наоборот. К числу таких механизмов относится параллелограмм Уатта , сконструированный изобретателем универсальной паровой машины Дж. Уаттом как раз для преобразования прямолинейного возвратно-поступательного движения штока (жёстко связанного с поршнем паровой машины) в качательное движение конца балансира. К середине XIX века подобных механизмов было известно немного, параметры их звеньев подбирались эмпирически, в то время как неизбежные неточности прямого хода приводили к росту потерь на трение и быстрому изнашиванию звеньев .

Чебышёв поставил задачу целенаправленного нахождения параметров искомого механизма с тем, чтобы на некотором заданном отрезке максимальное отклонение траектории рабочей точки механизма от её касательной в средней точке наименее уклонялось от нуля по сравнению с другими аналогичными траекториями. Решая данную задачу, учёный пришёл к созданию нового раздела теории приближения функций — теории функций, наименее уклоняющихся от нуля . Полученные результаты Чебышёв изложил в работе «Теория механизмов, известных под названием параллелограммов» (1854), став основоположником математической теории синтеза механизмов .

Методы теории функций, наименее уклоняющихся от нуля, П. Л. Чебышёв применил также в работах о центробежном регуляторе (где требовалось обеспечить изохронность хода механизма) и о зубчатых колёсах (для построения при помощи дуг окружностей профиля зуба, позволяющего добиться близости отношения угловых скоростей колёс к требуемому значению) .

Структура механизмов

Чебышёв положил также начало теории структуры плоских механизмов . В работе «О параллелограммах» (1869) он для рычажных механизмов с вращательными кинематическими парами и одной степенью свободы вывел структурную формулу (ныне известную как «формула Чебышёва» ) — тождество, которому должен удовлетворять каждый такой механизм:

${\displaystyle 3m-2(n+v)=1,}$

где ${\displaystyle m}$ — число подвижных звеньев, ${\displaystyle n}$ и ${\displaystyle v}$ — числа соответственно подвижных и неподвижных шарниров. Через 14 лет эта формула была переоткрыта немецким механиком М. Грюблером . В 1887 году ученик Чебышёва П. О. Сомов получил аналогичную структурную формулу для пространственных механизмов .

Конструирование механизмов

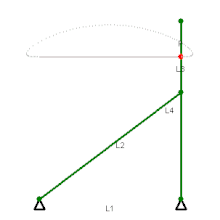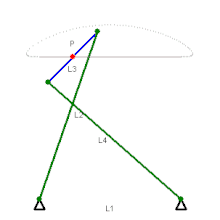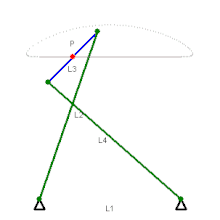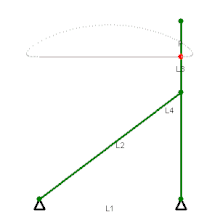
Чебышёву принадлежит создание свыше 40 различных механизмов и около 80 их модификаций. Среди них — механизмы с остановками, механизмы выпрямителей и ускорителей движения и тому подобные механизмы, многие из которых находят применение в современном авто-, мото- и приборостроении .

В конструкциях ряда механизмов, предложенных П. Л. Чебышёвым, нашли свою реализацию разработанные им методы синтеза механизмов. Здесь прежде всего заслуживают упоминания два приближённо-направляющих механизма Чебышёва , относящихся к классу шарнирных четырёхзвенников и известных под названиями лямбдаобразного и перекрёстного . В данных механизмах траектория заданной точки ${\displaystyle P}$ , расположенной на шатуне (у лямбдаобразного механизма — на конце шатуна, у перекрёстного — посередине), весьма мало отличается на некотором участке от отрезка прямой. В то же время минимальное число звеньев для механизма с вращательными кинематическими парами, обеспечивающее точное прямолинейное движение для одной из своих точек, равно 6 .

На Всемирной выставке в Филадельфии в 1876 году экспонировалась сконструированная Чебышёвым паровая машина , обладавшая рядом конструктивных преимуществ .

Среди созданных Чебышёвым механизмов — « стопоходящая машина » , имитировавшая движение животного при ходьбе . Эта машина была с успехом показана на Всемирной выставке в Париже в 1878 году, а в настоящее время хранится в московском Политехническом музее .

Модель инвалидной коляски — самокатное кресло, построенное П. Л. Чебышёвым, была показана на Всемирной выставке в Чикаго в 1893 году , а автоматический арифмометр , изобретённый им и ставший первым арифмометром непрерывного действия , хранится в Парижском музее искусств и ремёсел . Помимо самокатного кресла, на Чикагской выставке демонстрировались изобретённые П. Л. Чебышёвым сортировалка (механизм для сортировки зерна по массе) и семь механизмов для преобразования вращения в другие виды движения .

Педагогическая деятельность

В качестве члена Учёного комитета Министерства народного просвещения (1856—1873) П. Л. Чебышёв рецензировал учебники, составлял программы и инструкции для начальных и средних школ .

Во 2-й половине XIX века острейшая потребность в квалифицированных технических кадрах, вызванная бурным развитием машиностроения, поставила перед российской высшей школой вопрос о значительном увеличении числа подготавливаемых инженеров-машиностроителей. Профессор Киевского университета И. И. Рахманинов предложил готовить таких инженеров на физико-математических факультетах университетов. П. Л. Чебышёв выступил против этого предложения, считая более целесообразным сосредоточить подготовку инженеров в высших технических учебных заведениях, а в университетах готовить специалистов по фундаментальным наукам . Именно по этому пути — пути создания значительного числа технических вузов различного профиля — и пошла российская высшая школа .

Ученики Чебышёва

Для Чебышёва не меньшее значение, чем конкретные научные результаты, всегда имела задача развития российской математической школы. Как отмечали Б. В. Гнеденко и , «П. Л. Чебышёв был не только хорошим лектором, но и замечательным научным руководителем, обладавшим редкой способностью удачно выбирать и точно ставить перед молодыми исследователями новые вопросы, рассмотрение которых обещало привести к ценным открытиям» . Чебышёв стал одним из влиятельнейших членов Московского математического общества (создано в 1864 году, издавало первый в России математический журнал — « Математический сборник ») и оказывал обществу значительную помощь .

Значительный вклад в науку внесли многочисленные ученики П. Л. Чебышёва. Среди них — такие известные математики, механики и физики, как :

Чебышёв и его ученики сформировали ядро того научного коллектива математиков, за которым со временем закрепилось название Петербургской математической школы. В 1890 году члены данного коллектива организовали Санкт-Петербургское математическое общество . В 1893 году П. Л. Чебышёв был избран почётным членом этого общества.

Оценки и память

Заслуги Чебышёва оценены были учёным миром достойным образом. Характеристика его учёных заслуг очень хорошо выражена в записке академиков А. А. Маркова и И. Я. Сонина, зачитанной на первом после смерти Чебышёва заседании Академии. В этой записке сказано :

Труды Чебышёва носят отпечаток гениальности. Он изобрёл новые методы для решения многих трудных вопросов, которые были поставлены давно и оставались нерешёнными. Вместе с тем он поставил ряд новых вопросов, над разработкой которых трудился до конца своих дней.

Аналогичного взгляда на научный вклад П. Л. Чебышёва придерживались и другие известные математики XIX века. Так, Шарль Эрмит утверждал, что Чебышёв «является гордостью русской науки и одним из величайших математиков Европы», а Густав Миттаг-Леффлер писал, что Чебышёв — гениальный математик и один из величайших аналитиков всех времён .

Позднее академик В. А. Стеклов отмечал, что гений Чебышёва являет исключительный образец соединения практики с творческой, обобщающей силой увлечённого мышления .

Его избрали своим членом:

• Петербургская академия наук (1853),
• Берлинская академия наук (1871) ,
• Болонская академия наук (1873) ,
• Парижская академия наук (1874; член-корреспондент с 1860 ; эту честь Чебышёв разделил лишь ещё с одним русским учёным, знаменитым Бэром , избранным в 1876 году и в том же году скончавшимся) ,
• Лондонское королевское общество (1877) ,
• Шведская академия наук (1893)

и другие — всего 25 различных академий и научных обществ . Чебышёв состоял также почётным членом всех российских университетов; его портрет изображён на здании математико-механического факультета Санкт-Петербургского государственного университета .

П. Л. Чебышёв был награждён орденами Святого Александра Невского , Святого Владимира II степени, Святой Анны I степени, Святого Станислава I степени. В 1890 году он был также награждён французским орденом Почётного легиона .

Именем П. Л. Чебышёва названы:

• премия «За лучшие исследования в области математики и теории механизмов и машин», учреждённая Академией наук СССР в 1944 году (с 1997 года называется « Золотая медаль имени П. Л. Чебышёва »);
• кратер на Луне ;
• астероид (2010) Чебышёв ;
• математический журнал «Чебышёвский сборник» ;
• суперкомпьютер в Научно-исследовательском вычислительном центре МГУ ;
• многие объекты в современной математике;
• исследовательская лаборатория Санкт-Петербургского государственного университета ;
• Чебышёвская улица в Петергофе ( Санкт-Петербург ), а также улицы в Волгограде , Воронеже , Екатеринбурге , Калуге , Пензе , Твери ;
• горный хребет на острове Шпицберген ;
• общеобразовательная школа в деревне Машково, Жуковский район, Калужская область — соседняя деревня с родовым имением Чебышёва в деревне Спас-Проганье и местом его рождения в деревне Акатово .
• Премия Правительства Санкт-Петербурга за выдающиеся научные результаты в области науки и техники: в номинации математика и механика — премия им. П. Л. Чебышёва .
• Спас-Прогнанская муниципальная основная общеобразовательная школа Жуковского района Калужской области. В школе организован музей П. Л. Чебышёва.

На фасаде Дома академиков в Санкт-Петербурге , расположенном по адресу: 7-я линия Васильевского острова , 2/1, лит. А, установлена мемориальная доска с текстом: «Здесь жил академик Панфутий Львович Чебышев 1821—1894. Знаменитый математик, основатель русской школы теории чисел, теории вероятностей, теории механизмов и теории функций, сделавший основные открытия в этих науках» .

Публикации

Книги

См. также

Примечания

Литература

• Богатова Т. В. ЧЕБЫШЁВ Пафнутий Львович // Императорский Московский университет: 1755—1917: энциклопедический словарь / составители А. Ю. Андреев , Д. А. Цыганков . — М. : Российская политическая энциклопедия (РОССПЭН), 2010. — С. 814—815. — 894 с. — 2000 экз. — ISBN 978-5-8243-1429-8 .
• Боголюбов А. Н. . Математики. Механики. Биографический справочник. — Киев: Наукова думка , 1983. — 639 с.
• Глейзер Г. И. . . — М. : Просвещение , 1964. — 376 с.
• Глейзер Г. И. . История математики в школе. VII — VIII классы. — М. : Просвещение , 1982. — 240 с.
• Гнеденко Б. В. . Очерки по истории математики в России. 2-е изд. — М. : КомКнига, 2005. — ISBN 5-484-00123-4 . — С. 112—125.
• Головинский И. А. К обоснованию метода наименьших квадратов у П. Л. Чебышёва // Историко-математические исследования. — М. : Наука , 1986. — Вып. XXX . — С. 224—247 .
• Демьянов В. П. . Рыцарь точного знания (П. Л. Чебышёв). — М. : Знание , 1991. — 192 с. — ( Творцы науки и техники ). — ISBN 5-07-000060-8 .
• Жуков К. С. Разделы I, II, III // . — СПб. : Сохраненная культура, 2016. — С. 10—129. — 380 с. — ISBN 78-5-9908957 -9-9.
• История механики в России / Под ред. А. Н. Боголюбова , И. З. Штокало . — Киев: Наукова думка , 1987. — 392 с.
• Крылов А. Н. Пафнутий Львович Чебышёв // Наука и Жизнь : журнал. — 1945. — Январь (№ 1). — С. 44—48 .
• Майстров Л. Е. . Теория вероятностей. — Μ.: Наука , 1967. — 321 с.
• Марков А. А. , Сонин Н. Я. . Пафнутий Львович Чебышёв. Краткий биографический очерк // Чебышёв П. Л. Полное собрание сочинений. . — М. — Л. : Изд-во АН СССР, 1944. — 342 с. — С. 5—9.
• Математика XIX века : в 3 т. / Под ред. А. Н. Колмогорова , А. П. Юшкевича . — М. : Наука , 1978 (т. I), 1981 (т. II), 1987 (т. III).

• Т. I :
• Т. II :
• Т. III : Чебышёвское направление в теории функций. Обыкновенные дифференциальные уравнения. Вариационное исчисление. Теория конечных разностей

• Моисеев Н. Д. . Очерки развития механики. — М. : Издательство МГУ, 1961. — 478 с.
• Поссе К. А. // Энциклопедический словарь Брокгауза и Ефрона . — СПб. , 1903. — Т. XXXVIII (75) : Цензурный комитет — Человек. — С. 452—453.
• Прудников В. Е. П. Л. Чебышёв и Московский университет 40-х годов XIX века // Историко-математические исследования. Труды семинара МГУ по истории математики. Т. 1. — М. — Л. : ОГИЗ, 1948. — С. 184—214.
• Прудников В. Е. . . — Л. : Наука , 1976.
• Пырков В.Е. // Математика. — 2021. — Вып. 5(824) . — С. 35–38 .
• Рыбников К. А. . История математики. 2-е изд. — М. : Издательство МГУ, 1974. — 456 с.
• Садовничий В. А. Пафнутий Львович Чебышёв (1821—1894) // О людях Московского университета. — 3-е изд., дополненное. — М. : Издательство Московского университета, 2019. — С. 39—44. — 356 с. — 3000 экз. — ISBN 978-5-19-011397-6 .
• Стройк Д. Я. . . — М. : Наука , 1984. — 285 с.
• Тихомиров В. М. . Теория приближений // Современные проблемы математики. Фундаментальные направления. Т. 14. — М. : ВИНИТИ АН СССР, 1987. — 241 с. — (Итоги науки и техники). — С. 103—260.
• Трифонов В. В. Вклад братьев Чебышевых в развитие военной науки и техники. // Военно-исторический журнал . — 1987. — № 5. — С.88-91.
• Тюлина И. А. . История и методология механики. — М. : Издательство МГУ, 1979. — 282 с.
• Чебышев Пафнутий Львович / Б. В. Гнеденко // Чаган — Экс-ле-Бен. — М. : Советская энциклопедия, 1978. — ( Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 29).

Ссылки

• (неопр.) . // Tcheb.ru. Дата обращения: 26 февраля 2014. 23 августа 2011 года.
• (неопр.) (мультфильм, объясняющий принцип работы). // Математические этюды . Дата обращения: 26 февраля 2014.
• (неопр.) . // ИС АРАН . Дата обращения: 26 февраля 2014.
• (неопр.) . // Mathinfinity. — Краткая биография и основные работы . Дата обращения: 26 февраля 2014.
• (неопр.) . // Научное наследие России. — Биография и публикации . Дата обращения: 26 февраля 2014.
• (неопр.) . // ТГПУ имени Л. Н. Толстого . Дата обращения: 26 февраля 2014.
• Ширяев А. Н. // Теория вероятн. и её примен., 66:4 (2021), 625–635