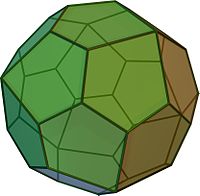
Пентагона́льный гексеконта́эдр (от др.-греч. πέντε — «пять», γωνία — «угол», ἑξήκοντα — «шестьдесят» и ἕδρα — «грань») — полуправильный многогранник (каталаново тело), двойственный курносому додекаэдру . Составлен из 60 одинаковых неправильных пятиугольников .

Имеет 92 вершины. В 12 вершинах (расположенных так же, как вершины икосаэдра ) сходятся по 5 граней своими острыми углами; в 20 вершинах (расположенных так же, как вершины додекаэдра ) сходятся по 3 грани теми тупыми углами, которые дальше от острого; в остальных 60 вершинах две грани сходятся своими тупыми углами, ближними к острому, и одна — тупым углом, дальним от острого.

• 
  12 вершин расположены так же, как вершины икосаэдра
• 
  20 вершин расположены так же, как вершины додекаэдра

У пентагонального гексеконтаэдра 150 рёбер — 60 «длинных» и 90 «коротких».

В отличие от большинства других каталановых тел, пентагональный гексеконтаэдр (наряду с пентагональным икоситетраэдром ) является хиральным и существует в двух разных зеркально-симметричных (энантиоморфных) вариантах — «правом» и «левом».

Метрические характеристики и углы

При определении метрических свойств пентагонального гексеконтаэдра приходится решать кубические уравнения и пользоваться кубическими корнями — тогда как для ахиральных каталановых тел не требуется ничего сложнее квадратных уравнений и квадратных корней . Поэтому пентагональный гексеконтаэдр, в отличие от большинства других каталановых тел, не допускает евклидова построения . То же верно и для пентагонального икоситетраэдра, а также для двойственных им архимедовых тел.

В формулах ниже константа ${\displaystyle \xi }$ — единственный вещественный корень уравнения

${\displaystyle 8x^{3}+8x^{2}=\Phi ^{2},}$

где ${\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}$ — отношение золотого сечения ; этот корень равен

${\displaystyle \xi ={\frac {1}{12}}\left({\sqrt[{3}]{44+12\Phi \,(9+{\sqrt {81\Phi -15}})}}+{\sqrt[{3}]{44+12\Phi \,(9-{\sqrt {81\Phi -15}})}}-4\right)\approx 0{,}4715756.}$

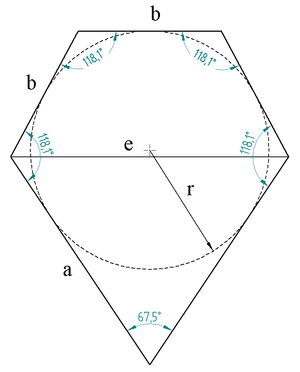
Если три «коротких» стороны грани имеют длину ${\displaystyle b}$ , то две «длинных» стороны имеют длину

${\displaystyle a={\frac {1+2\xi }{2(1-2\xi ^{2})}}b\approx 1{,}7498526b.}$

Площадь поверхности и объём многогранника при этом выражаются как

${\displaystyle S={\frac {30(2+3\xi){\sqrt {1-\xi ^{2}}}}{1-2\xi ^{2}}}\;b^{2}\approx 162{,}6989642b^{2},}$

${\displaystyle V={\frac {5(1+\xi)(2+3\xi)}{(1-2\xi ^{2}){\sqrt {1-2\xi }}}}\;b^{3}\approx 189{,}7898521b^{3}.}$

Радиус вписанной сферы (касающейся всех граней многогранника в их инцентрах ) при этом будет равен

${\displaystyle r={\frac {1}{2}}{\sqrt {\frac {1+\xi }{(1-\xi)(1-2\xi)}}}\;b\approx 3{,}4995278b,}$

радиус полувписанной сферы (касающейся всех рёбер) —

${\displaystyle \rho ={\sqrt {\frac {1+\xi }{2(1-2\xi)}}}\;b\approx 3{,}5976248b,}$

радиус окружности, вписанной в грань —

${\displaystyle r_{\Gamma \mathrm {P} }={\sqrt {\rho ^{2}-r^{2}}}={\frac {1}{2}}{\sqrt {\frac {1+\xi }{1-\xi }}}\;b\approx 0{,}8343915b,}$

диагональ грани, параллельная одной из «коротких» сторон —

${\displaystyle e=(1+2\xi)b\approx 1{,}9431513b.}$

Описать около пентагонального гексеконтаэдра сферу — так, чтобы она проходила через все вершины, — невозможно.

Все четыре тупых угла грани равны ${\displaystyle \arccos \,(-\xi)\approx 118{,}14^{\circ };}$ острый угол грани (между «длинными» сторонами) равен ${\displaystyle \arccos \,(8\xi ^{2}-8\xi ^{4}-1)\approx 67{,}45^{\circ }.}$

Двугранный угол при любом ребре одинаков и равен ${\displaystyle \arccos \,{\frac {\xi }{\xi -1}}\approx 153{,}18^{\circ }.}$

Примечания

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .