Пятиска́тная пряма́я бирото́нда — один из многогранников Джонсона ( J ₃₄ , по Залгаллеру — 2М ₉ ).

Составлена из 32 граней: 20 правильных треугольников и 12 правильных пятиугольников . Среди пятиугольных граней 2 окружены пятью треугольными, остальные 10 — пятиугольной и четырьмя треугольными; среди треугольных граней 10 окружены тремя пятиугольными, другие 10 — двумя пятиугольными и треугольной.

Имеет 60 рёбер одинаковой длины. 5 рёбер располагаются между двумя пятиугольными гранями, 50 рёбер — между пятиугольной и треугольной, 5 рёбер — между двумя треугольными.

У пятискатной прямой биротонды 30 вершин. В каждой сходятся две пятиугольных и две треугольных грани.

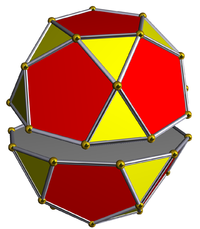
Пятискатную прямую биротонду можно получить из икосододекаэдра , разделив его на две половины, каждая из которых представляет собой пятискатную ротонду ( J ₆ ), и повернув одну из них на 36° вокруг её оси симметрии.

Объём и площадь поверхности при этом не изменятся; описанная и полувписанная сферы полученного многогранника также совпадают с описанной и полувписанной сферами исходного икосододекаэдра.

Метрические характеристики

Если пятискатная прямая биротонда имеет ребро длины ${\displaystyle a}$ , её площадь поверхности и объём выражаются как

${\displaystyle S=\left(5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}\approx 29{,}3059828a^{2},}$

${\displaystyle V={\frac {1}{6}}\left(45+17{\sqrt {5}}\right)a^{3}\approx 13{,}8355259a^{3}.}$

Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен

${\displaystyle R={\frac {1}{2}}\left(1+{\sqrt {5}}\right)a\approx 1{,}6180340a;}$

радиус полувписанной сферы (касающейся всех рёбер в их серединах) —

${\displaystyle \rho ={\frac {1}{2}}{\sqrt {5+2{\sqrt {5}}}}\;a\approx 1{,}5388418a.}$

Примечания

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .