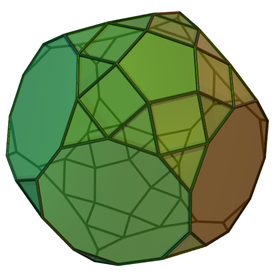
Три́жды наращённый усечённый додека́эдр — один из многогранников Джонсона ( J ₇₁ , по Залгаллеру — М ₁₂ +3М ₆ ).

Составлен из 62 граней: 35 правильных треугольников , 15 квадратов , 3 правильных пятиугольников и 9 правильных десятиугольников . Среди десятиугольных граней 3 окружены четырьмя десятиугольными и шестью треугольными, остальные 6 — тремя десятиугольными и семью треугольными; каждая пятиугольная грань окружена пятью квадратными; каждая квадратная грань окружена пятиугольной и тремя треугольными; среди треугольных 5 граней окружены тремя десятиугольными, 15 граней — двумя десятиугольными и квадратной, остальные 15 — десятиугольной и двумя квадратными.

Имеет 135 рёбер одинаковой длины. 15 рёбер располагаются между двумя десятиугольными гранями, 60 рёбер — между десятиугольной и треугольной, 15 рёбер — между пятиугольной и квадратной, остальные 45 — между квадратной и треугольной.

У трижды наращённого усечённого додекаэдра 75 вершин. В 30 вершинах сходятся две десятиугольных грани и одна треугольная; в 30 вершинах сходятся десятиугольная, квадратная и две треугольных грани; в 15 вершинах сходятся пятиугольная, две квадратных и треугольная грани.

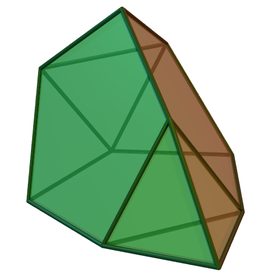
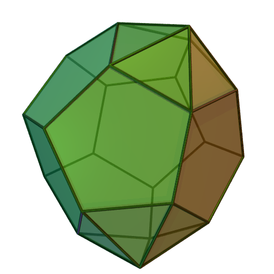
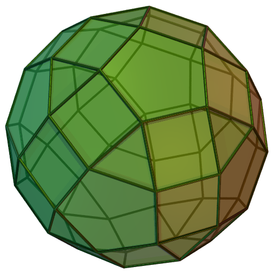
Трижды наращённый усечённый додекаэдр можно получить из четырёх многогранников — усечённого додекаэдра и трёх пятискатных куполов ( J ₅ ), — приложив куполы к любым трём попарно не смежным десятиугольным граням усечённого додекаэдра.

Метрические характеристики

Если трижды наращённый усечённый додекаэдр имеет ребро длины ${\displaystyle a}$ , его площадь поверхности и объём выражаются как

${\displaystyle S={\frac {1}{4}}\left(60+35{\sqrt {3}}+3\left(30+{\sqrt {5}}\right){\sqrt {5+2{\sqrt {5}}}}\right)a^{2}\approx 104{,}5647564a^{2},}$

${\displaystyle V={\frac {7}{12}}\left(75+37{\sqrt {5}}\right)a^{3}\approx 92{,}0118005a^{3}.}$

Примечательные свойства

Среди всех многогранников Джонсона с заданной длиной ребра трижды наращённый усечённый додекаэдр имеет наибольший объём и наибольшую площадь поверхности.

Среди всех многогранников Джонсона трижды наращённый усечённый додекаэдр имеет наибольшее число вершин и наибольшее число рёбер (по числу же граней — делит первое место с J 72 , J 73 , J 74 , J 75 ).

Примечания

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .