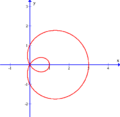
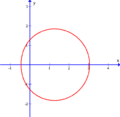
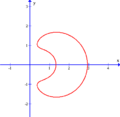
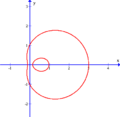
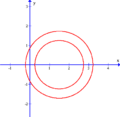
Ова́л Дека́рта — плоская алгебраическая кривая четвёртого порядка, представляющая собой геометрическое место точек , для которых сумма расстояний ${\displaystyle r_{1}}$ и ${\displaystyle r_{2}}$ до двух точек ${\displaystyle F_{1}}$ и ${\displaystyle F_{2}}$ , называемых фокусами , помноженных на константы ${\displaystyle p_{1}}$ и ${\displaystyle p_{2}}$ , является постоянной, то есть:

${\displaystyle p_{1}r_{1}+p_{2}r_{2}=d.}$

Уравнение кривой

Эта кривая описывается уравнением

${\displaystyle (x^{2}+y^{2}-2ax)^{2}=b^{2}(x^{2}+y^{2})+c,}$

где a , b и c — константы, связанные с параметрами p ₁ , p ₂ и d .

При ${\displaystyle c=0}$ овал Декарта представляет собой улитку Паскаля .

Если ${\displaystyle p_{1}=p_{2},}$ , то овал Декарта представляет собой эллипс , в случае ${\displaystyle p_{1}=-p_{2},}$ — гиперболу .

Эту кривую первым изучил и описал Рене Декарт в 1637 году. Эти овалы Декарт построил при решении задачи оптики: он искал кривую, которая преломляла бы лучи, выходящие из одной точки, так, чтобы преломленные лучи проходили бы через другую заданную точку.

Примеры овалов Декарта

• 
  a = 1, b = 1, c = 0
• 
  a = 1, b = 1, c = 1
• 
  a = 1, b = 1, c = −1
• 
  a = 1, b = 1, c = 0,05
• 
  a = 1,5, b = 0, c = 0,5

См. также

• Овал
• Овал Кассини
• Декартов лист

Ссылки

• Д. К. Бобылёв . // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб. , 1890—1907.
• от 19 февраля 2012 на Wayback Machine (англ.)