Interested Article - Середина отрезка

Средняя точка отрезка с вершинами ( x ₁ , y ₁ ) и ( x ₂ , y ₂ )

Середина отрезка — точка на заданном отрезке , находящаяся на равном расстоянии от обоих концов данного отрезка. Является центром масс как всего отрезка, так и его конечных точек.

Координаты

Средняя точка отрезка в $n$ $n$ -мерном пространстве, концами которого являются точки $A=(a_{1},a_{2},\dots ,a_{n})$ $A=(a_{1},a_{2},\dots ,a_{n})$ и $B=(b_{1},b_{2},\dots ,b_{n})$ $B=(b_{1},b_{2},\dots ,b_{n})$ , задаётся формулой:

{\frac {A+B}{2}}

{\frac {A+B}{2}}

.

Таким образом, $i$ $i$ -я координата средней точки ( $i=1,2,\dots ,n$ $i=1,2,\dots ,n$ ) равна:

{\frac {a_{i}+b_{i}}{2}}

{\frac {a_{i}+b_{i}}{2}}

.

Построение

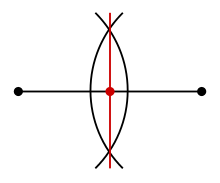
Если заданы две точки, нахождение середины образованного ими отрезка может быть осуществлено с помощью циркуля и линейки . Для нахождения середины отрезка на плоскости можно сначала построить две дуги равного (и достаточно большого) радиуса с центрами в концах отрезка, а затем через точки пересечения этих дуг провести прямую. Точка, где полученная прямая пересекает отрезок, является его серединой.

С использованием теоремы Мора — Маскерони возможно также нахождение середины отрезка с помощью одного только циркуля: на первом шаге для отрезка $(AB)$ $(AB)$ строится точка $C$ $C$ , симметричная точке $A$ $A$ относительно точки $B$ $B$ ; на втором шаге строится инверсия точки $C$ $C$ относительно окружности радиуса $|AB|$ $|AB|$ с центром в точке $A$ $A$ ; полученная точка является серединой отрезка $(AB)$ $(AB)$ .

Можно также построить середину отрезка с помощью только линейки при условии, что на плоскости имеется окружность с отмеченным центром .

Геометрические свойства

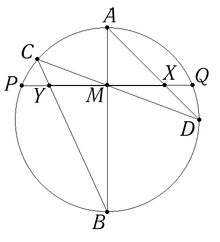
Середина любого диаметра окружности является центром окружности. Перпендикуляр к любой хорде , проходящий через её середину, проходит через центр окружности. Теорема о бабочке утверждает, что если $M$ $M$ является серединой хорды $PQ$ $PQ$ и через середину проходят две другие хорды $AB$ $AB$ и $CD$ $CD$ , то $AD$ $AD$ и $BC$ $BC$ пересекают хорду $PQ$ $PQ$ в точках $X$ $X$ и $Y$ $Y$ соответственно таким образом, что $M$ $M$ является серединой отрезка $XY$ $XY$ .

Центр эллипса является серединой отрезка, соединяющего два фокуса эллипса.

Середина отрезка, соединяющего вершины гиперболы , является центром гиперболы.

Перпендикуляры к серединам сторон треугольника пересекаются в одной точке, и эта точка является центром описанной окружности . Центр девяти точек треугольника — середина отрезка, соединяющего центра описанной окружности с ортоцентром данного треугольника. Вершины серединного треугольника данного треугольника лежат в серединах сторон треугольника.

В прямоугольном треугольнике центр описанной окружности является серединой гипотенузы . В равнобедренном треугольнике медиана, высота и биссектриса угла при вершине совпадают с прямой Эйлера и осью симметрии , и эта прямая проходит через середину основания.

Две бимедианы выпуклого четырёхугольника — это отрезки, соединяющие середины противоположных сторон. Две бимедианы и отрезок, соединяющий середины диагоналей, пересекаются в одной точке, которая является серединой этих трёх отрезков . Теорема Брахмагупты утверждает, что если вписанный в окружность четырёхугольник является ортодиагональным (то есть, имеющий перпендикулярные диагонали ), то перпендикуляры к сторонам из точки пересечения диагоналей всегда проходят через середину противоположной стороны. Теорема Вариньона утверждает, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма , а если четырёхугольник к тому же является самонепересекающимся, то площадь параллелограмма равна половине площади четырёхугольника. Прямая Ньютона — линия, соединяющая середины двух диагоналей выпуклого четырёхугольника, не являющегося параллелограммом. Отрезки, соединяющие середины противоположных сторон выпуклого четырёхугольника, пересекаются в точке, лежащей на прямой Ньютона.

Правильный многоугольник имеет вписанную окружность , которая касается всех сторон многоугольника в серединах его сторон. В правильном многоугольнике с чётным числом сторон середины диагоналей , соединяющих противоположные центры, являются центром многоугольника. Серединный многоугольник — многоугольник, вершины которого — середины рёбер исходного многоугольника. Растянутый многоугольник серединных точек вписанного многоугольника P является другим вписанным многоугольником, вписанным в ту же окружность, и его вершины являются серединами дуг между вершинами P . Повторение операции создания многоугольника растянутых средних точек приводит к последовательности многоугольников, форма которых сходится к правильному многоугольнику .

Обобщения

Середина отрезка является аффинным инвариантом , поэтому координатные формулы применимы к любой аффинной системе координат .

Середину отрезка невозможно определить в проективной геометрии : любая внутренняя точка отрезка может быть проективно отображена в любую другую точку внутри (того же или любого другого) проективного отрезка. Закрепление одной такой точки в качестве середины определяет аффинную структуру на проективной прямой , содержащей этот отрезок. Четвёртая точка гармонической четвёрки для такой «средней точки» и двух конечных точек является бесконечно удалённой точкой .

Понятие середины отрезка можно ввести на геодезических в римановом многообразии , но в отличие от аффинного случая, середина отрезка может быть не единственной.

Примечания

, с. 20.
, с. 172—179.
(неопр.) (29 сентября 2010). Дата обращения: 20 июля 2015. Архивировано из 25 ноября 2016 года.
, с. 67—72.
.
↑ , с. 255—270.
.
, с. 119.

Литература

А. Н. Костовский. Геометрические построения одним циркулем. — М. : «Наука» Главная редакция физико-математической литературы, 1984. — (Популярные лекции по математике).
Август Адлер. Теория геометрических построений. — Ленинград: Государственное учебно-педагогическое издательство Наркомпроса РСФСР, Ленинградское отделение, 1940.
Р. Курант, Г. Роббинс. Что такое математика?. — 3-е. — МЦНМО, 2001. — ISBN 5–900916–45–6.
Jiu Ding, L. Richard Hitt, Xin-Min Zhang. // Linear Algebra and its Applications. — 2003. — Т. 367 . — doi : .
Francisco Gomez-Martin, Perouz Taslakian, Godfried T. Toussaint. . — 2008.
H. S. M. Coxeter . The Real Projective Plane. — New York, Toronto, London: McGraw-Hill, 1949.
Х. С. М. Коксетер. Действительная проективная плоскость. — М. : Физматлит, 1959.
Nathan Altshiller-Court. College Geometry. — Mineola, New York: Dover Publ., 2007. — ISBN 0-486-45805-9 .