Квантовая механика
Математические основы
Основа Классическая механика Постоянная Планка Интерференция Бра и кет Гамильтониан Старая квантовая теория
Фундаментальные понятия Квантовое состояние Квантовая наблюдаемая Волновая функция Квантовая суперпозиция Квантовая запутанность Смешанное состояние Измерение Неопределённость Принцип Паули Дуализм Декогеренция Симметрия Теорема Эренфеста Туннельный эффект
Эксперименты Опыт Дэвиссона — Джермера Опыт Франка — Герца Опыт Штерна — Герлаха Опыт Юнга Квантовый ластик Квантовый ластик с отложенным выбором Проверка неравенств Белла Фотоэффект
Формулировки Представление Шрёдингера Представление Гейзенберга Представление взаимодействия Представление фазового пространства Матричная квантовая механика Интегралы по траекториям Диаграммы Фейнмана
Уравнения Шрёдингера Паули Клейна — Гордона Дирака Швингера — Томонаги фон Неймана Блоха Линдблада Гейзенберга
Интерпретации Копенгагенская Теория скрытых параметров Супердетерминизм Многомировая Теория де Бройля — Бома
Развитие теории Квантовая теория поля Квантовая электродинамика Теория Глэшоу — Вайнберга — Салама Квантовая хромодинамика Стандартная модель Квантовая гравитация
Сложные темы Релятивистская квантовая механика Квантовая теория поля Квантовая гравитация Теория всего
Известные учёные Планк Эйнштейн Шрёдингер Гейзенберг Йордан Бор Паули Дирак Фок Борн де Бройль Ландау Фейнман Бом Эверетт
См. также История возникновения ЭПР-парадокс
См. также: Портал:Физика

Эффе́кт Ко́мптона ( ко́мптон-эффе́кт , ко́мптоновское рассе́яние ) — упругое рассеяние фотона заряженной частицей, обычно электроном , названное в честь первооткрывателя Артура Холли Комптона . Если рассеяние приводит к уменьшению энергии , поскольку часть энергии фотона передаётся отражающемуся электрону, что соответствует увеличению длины волны фотона (который может быть рентгеновским или гамма- фотоном ), то этот процесс называется эффектом Комптона . Обратное комптоновское рассеяние происходит, когда заряженная частица передаёт фотону часть своей энергии, что соответствует уменьшению длины волны кванта света.

Обнаружен американским физиком Артуром Комптоном в 1923 году в экспериментах с рентгеновским излучением ; за это открытие Комптон стал лауреатом Нобелевской премии по физике за 1927 год .

Эффект Комптона по природе подобен фотоэффекту — разница заключается в том, что при фотоэффекте фотон полностью поглощается электроном, тогда как при комптоновском рассеянии он только меняет направление движения и энергию .

Вступление

Комптоновское рассеяние является примером упругого рассеяния света на свободной заряженной частице, где длина волны рассеянного света отличается от длины волны падающего излучения. В первоначальном эксперименте Комптона (см. Рис. 1) энергия рентгеновского фотона (≈17 кэВ) была намного больше, чем энергия связи атомного электрона, поэтому электроны можно было считать свободными после рассеяния. Величина, на которую изменяется длина волны света, называется комптоновским сдвигом . Хотя ядерное комптоновское рассеяние существует , комптоновское рассеяние обычно относится к взаимодействию, в котором участвуют только электроны атома.

Эффект наблюдал Артур Холли Комптон в 1923 году в Вашингтонском университете в Сент-Луисе и в последующие годы этот эффект подтвердил его аспирант . Комптон получил Нобелевскую премию по физике 1927 года за своё открытие.

Этот эффект демонстрирует, что свет не может быть объяснён исключительно как волновое явление . Томсоновское рассеяние , следующее из классической теории рассеяния электромагнитных волн заряженными частицами, не может объяснить сдвиги в длине волны при низкой интенсивности, потому что классически свет должен быть достаточной интенсивности для того, чтобы электрическое поле ускоряло заряженную частицу до релятивистской скорости, вызывало отдачу из-за радиационного давления и связанный с ним доплеровский сдвиг рассеянного света , но эффект стал бы сколь угодно малым при достаточно низких интенсивностях света независимо от длины волны . Таким образом, свет ведёт себя так, как будто он состоит из частиц, что объясняет низкоинтенсивное комптоновское рассеяние. Или предположение, что электрон можно рассматривать как свободный, неверно, что приводит к фактически бесконечной массе электрона, равной массе ядра (см., например, комментарий ниже об упругом рассеянии рентгеновских лучей, вызванном этим эффектом). Эксперимент Комптона убедил физиков в том, что свет можно рассматривать как поток частицеподобных объектов (квантов, называемых фотонами), энергия которых пропорциональна частоте световой волны.

Как показано на рис.2, взаимодействие между электроном и фотоном приводит к тому, что электрон получает часть энергии, а фотон с оставшейся энергией излучается в направлении, отличном от исходного, так что общий импульс системы также сохраняется. Если у рассеянного фотона ещё достаточно энергии, процесс может повториться. В этом сценарии электрон рассматривается как свободный или слабосвязанный. Экспериментальная проверка сохранения импульса в отдельных процессах комптоновского рассеяния Боте и Гейгером, а также Комптоном и Саймоном была важна для опровержения , которая основывалась на старой квантовой теории.

Комптоновское рассеяние — один из трёх конкурирующих процессов при взаимодействии фотонов с веществом. При энергиях от нескольких эВ до нескольких кэВ, соответствующих спектру от видимого света до мягкого рентгеновского излучения, фотон может быть полностью поглощён, а его энергия может оторвать электрон от основного атома, процесс, известный как фотоэффект . Фотоны высокой энергии 1,022 МэВ и выше могут бомбардировать ядро и вызывать образование электрон-позитронной пары. Этот процесс называется рождением пар . Комптоновское рассеяние является наиболее важным процессом при взаимодействии в промежуточной области энергий.

Описание явления

К началу 20-го века исследования взаимодействия рентгеновских лучей с веществом шли полным ходом. Было замечено, что когда рентгеновские лучи известной длины волны взаимодействуют с атомами, рентгеновские лучи рассеиваются под углом ${\displaystyle \theta }$ и длина волны рассеянного кванта связана с ${\displaystyle \theta }$ . Хотя классический электромагнетизм предсказывал, что длина волны рассеянных лучей должна быть равна начальной длине волны , многочисленные эксперименты показали, что длина волны рассеянных лучей была больше (что соответствовало более низкой энергии), чем исходная длина волны.

В 1923 году Комптон опубликовал в Physical Review статью, в которой объяснил рентгеновский сдвиг, приписывая частицеподобный импульс световым квантам. Эйнштейн предложил световые кванты в 1905 году для объяснения фотоэффекта, но Комптон не основывался на работе Эйнштейна. Энергия световых квантов зависит только от частоты света. В своей статье Комптон вывел математическую связь между сдвигом длины волны и углом рассеяния рентгеновских лучей, предположив, что каждый рассеянный рентгеновский фотон взаимодействует только с одним электроном. Его статья завершается отчётом об экспериментах, которые подтвердили полученное им соотношение:

${\displaystyle \lambda '-\lambda ={\frac {h}{m_{e}c}}(1-\cos {\theta })~,}$

где: ${\displaystyle \lambda }$ — начальная длина волны,

${\displaystyle \lambda '}$ — длина волны после рассеяния,

${\displaystyle h}$ — постоянная Планка ,

${\displaystyle m_{e}}$ — масса покоя электрона ,

${\displaystyle c}$ — скорость света

${\displaystyle \theta }$ — угол рассеяния.

Величина ${\displaystyle {\frac {h}{m_{e}c}}}$ известна как комптоновская длина волны электрона; она равна 2,43⋅10 ⁻¹² м . Сдвиг длины волны ${\displaystyle (\lambda '-\lambda)}$ равен по крайней мере нулю ( ${\displaystyle \theta }$ =0°) и не более чем в два раза превышает комптоновскую длину волны электрона ( ${\displaystyle \theta }$ =180°).

Комптон обнаружил, что у некоторых рентгеновских лучей не наблюдается сдвиг длины волны, несмотря на то, что они рассеиваются на большие углы; в каждом из этих случаев фотон не мог выбить электрон . Таким образом, величина этого сдвига связана не с комптоновской длиной волны электрона, а с комптоновской длиной волны всего атома, которая может быть в 10000 раз меньше. Это известно как «когерентное» рассеяние на всём атоме, поскольку атом остается неповреждённым и не получает внутреннего возбуждения.

В первоначальных экспериментах Комптона, приведённых выше, непосредственно измерялся сдвиг длины волны. В современных экспериментах принято измерять энергии, а не длины волн рассеянных фотонов. Для данной энергии падающего кванта ${\displaystyle E_{\gamma }=hc/\lambda ,}$ энергия исходящего фотона в конечном состоянии, ${\displaystyle E_{\gamma ^{\prime }}}$ , задаётся как:

${\displaystyle E_{\gamma ^{\prime }}={\frac {E_{\gamma }}{1+(E_{\gamma }/m_{e}c^{2})(1-\cos \theta)}}~.}$

Невозможность классического толкования

В классической электродинамике взаимодействие электрона с электромагнитной волной , при учёте только электрической составляющей, описывается следующим образом: под действием периодических возмущений, электрон начинает колебаться с той же частотой, что и набегающая волна, и излучать новые электромагнитные волны той же частоты.

Если учесть в том числе и магнитное поле , то движение электрона будет описываться сложным дифференциальным уравнением , и, в случае если поле достаточно сильное, чтобы разогнать электрон до релятивистских скоростей , электрон может начинать излучать на частотах, отличных от частоты начальной волны .

Однако ни в коем случае классическая теория не предполагает существование у электронов отдачи — волна распределена в пространстве и не может «сконцентрироваться» на одном электроне и выбить его из атома. Поэтому регистрация таких электронов точно указывает на неполноту классического описания, а именно, на корпускулярно-волновую природу света .

Квазиклассический подход позволяет получить только изменение длины волны рассеянного фотона. Для вычисления сечения рассеяния необходимо применить уравнения квантовой электродинамики . Такое распределение даёт Формула Клейна — Нишины .

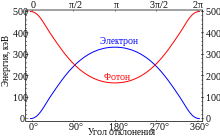
При росте энергии фотона вероятность рассеяния постепенно уменьшается, причём вероятность рассеяния на большие углы уменьшается быстрее.

Угол рассеяния электрона отдачи отличается от угла рассеяния фотона, и, в случае рассеяния на свободном электроне, описывается уравнением :

${\displaystyle {\mbox{tg}}\phi ={\frac {{\mbox{ctg}}(\theta /2)}{1+h\nu /(m_{e}c^{2})}}~,}$

где ${\displaystyle \theta }$ — угол рассеяния фотона.

Вывод формулы рассеяния

Фотон γ с длиной волны λ сталкивается с электроном e в атоме, который рассматривается как покоящийся. Столкновение заставляет электрон испытывать отдачу , и новый фотон γ ' с длиной волны λ ' отлетает под углом θ к первоначальному направлению движения фотона. (Далее e ' — электрон после столкновения.) Комптон допускал возможность того, что взаимодействие иногда ускоряет электрон до скоростей, достаточно близких к скорости света, что требует применения специальной теории относительности Эйнштейна для правильного описания его энергии и импульса.

В заключение статьи Комптона 1923 года он сообщил о результатах экспериментов, подтверждающих предсказания его формулы рассеяния, тем самым подтверждая предположение, что фотоны несут импульс, а также энергию в виде квантов. В начале своего вывода он постулировал выражение для импульса фотона, приравнивая уже установленное Эйнштейном соотношение массы и энергии ${\displaystyle E=mc^{2}}$ квантованным энергиям фотонов ${\displaystyle hf,}$ которое Эйнштейн постулировал отдельно. Если ${\displaystyle mc^{2}=hf,}$ то эквивалентная масса фотона должна быть ${\displaystyle hf/c^{2}.}$ Тогда импульс фотона равен этой эффективной массе, умноженной на инвариантную скорость ${\displaystyle c}$ фотона. Для фотона его импульс ${\displaystyle p=hf/c,}$ и, таким образом, ${\displaystyle hf}$ можно заменить на ${\displaystyle pc}$ для всех слагаемых содержащих импульс фотона, которые возникают в процессе вывода, приведённого ниже. Вывод, который появляется в статье Комптона, более краток, но следует той же логике в той же последовательности, что и приведённый вывод.

Закон сохранения энергии ${\displaystyle E}$ просто уравнивает сумму энергий до и после рассеяния:

${\displaystyle E_{\gamma }+E_{e}=E_{\gamma '}+E_{e'}~.\!}$

Комптон постулировал, что фотоны несут импульс и таким образом, из закона сохранения импульса , импульсы частиц должны быть аналогичным образом связаны соотношением:

${\displaystyle \mathbf {p} _{\gamma }=\mathbf {p} _{\gamma '}+\mathbf {p} _{e'}~,}$

в котором первоначальный импульс электрона ${\displaystyle {p_{e}}}$ опускается в предположении, что он фактически равен нулю.

Энергии фотонов связаны с частотами соотношениями:

${\displaystyle E_{\gamma }=hf\!}$

${\displaystyle E_{\gamma '}=hf'\!~,}$

где ${\displaystyle h}$ — постоянная Планка .

Перед событием рассеяния электрон рассматривается как достаточно близкий к состоянию покоя, так что его полная энергия полностью состоит из его массы покоя, исходя из его энергии для ${\displaystyle m_{e}}$ получается:

${\displaystyle E_{e}=m_{e}c^{2}~.\!}$

После рассеяния существует возможность того, что электрон может быть ускорен до значительной доли от скорости света, что означает, что его полная энергия должна быть представлена с использованием релятивистского в виде:

${\displaystyle E_{e'}={\sqrt {(p_{e'}c)^{2}+(m_{e}c^{2})^{2}}}~.}$

После подстановки этих величин в выражение для сохранения энергии получается:

${\displaystyle hf+m_{e}c^{2}=hf'+{\sqrt {(p_{e'}c)^{2}+(m_{e}c^{2})^{2}}}~.}$

Это выражение можно использовать, чтобы найти величину импульса рассеянного электрона:

${\displaystyle p_{e'}^{\,2}c^{2}=(hf-hf'+m_{e}c^{2})^{2}-m_{e}^{2}c^{4}~.\qquad \qquad (1)\!}$

Эта величина импульса, полученного электроном (ранее равная нулю), превышает отношение энергию/c, потерянную фотоном:

${\displaystyle {\frac {1}{c}}{\sqrt {(hf-hf'+m_{e}c^{2})^{2}-m_{e}^{2}c^{4}}}>{\frac {hf-hf'}{c}}~.}$

Уравнение (1) связывает различные энергии, рассмотренные при столкновении. Изменение импульса электрона включает релятивистское изменение энергии электрона, поэтому оно не связано просто с изменением энергии, происходящим в классической физике. Изменение величины импульса фотона связано не только с изменением его энергии, оно также предполагает изменение направления.

Решение уравнения для сохранения импульса относительно импульса рассеянного электрона приводит к:

${\displaystyle \mathbf {p} _{e'}=\mathbf {p} _{\gamma }-\mathbf {p} _{\gamma '}~.}$

Использование скалярного произведения даёт квадрат его величины:

${\displaystyle {\begin{aligned}p_{e'}^{\,2}&=\mathbf {p} _{e'}\cdot \mathbf {p} _{e'}=(\mathbf {p} _{\gamma }-\mathbf {p} _{\gamma '})\cdot (\mathbf {p} _{\gamma }-\mathbf {p} _{\gamma '})\\&=p_{\gamma }^{\,2}+p_{\gamma '}^{\,2}-2p_{\gamma }\,p_{\gamma '}\cos \theta ~.\end{aligned}}}$

${\displaystyle p_{\gamma }c}$ заменяется ${\displaystyle hf,}$ и, умножая обе части на ${\displaystyle c^{2},}$ получается :

${\displaystyle p_{e'}^{\,2}c^{2}=p_{\gamma }^{\,2}c^{2}+p_{\gamma '}^{\,2}c^{2}-2c^{2}p_{\gamma }\,p_{\gamma '}\cos \theta ~.}$

После замены слагаемых с импульсом фотона на ${\displaystyle hf/c}$ , получается второе выражение для величины импульса рассеянного электрона:

${\displaystyle p_{e'}^{\,2}c^{2}=(hf)^{2}+(hf')^{2}-2(hf)(hf')\cos {\theta }~.\qquad \qquad (2)}$

Приравнивая альтернативные выражения для этого импульса, получается выражение:

${\displaystyle (hf-hf'+m_{e}c^{2})^{2}-m_{e}^{\,2}c^{4}=\left(hf\right)^{2}+\left(hf'\right)^{2}-2h^{2}ff'\cos {\theta }~,}$

которое после раскрытия квадрата и перестановки членов преобразуется к виду:

${\displaystyle 2hfm_{e}c^{2}-2hf'm_{e}c^{2}=2h^{2}ff'\left(1-\cos \theta \right)~.}$

Разделив обе стороны на ${\displaystyle 2hff'm_{e}c}$ получается:

${\displaystyle {\frac {c}{f'}}-{\frac {c}{f}}={\frac {h}{m_{e}c}}\left(1-\cos \theta \right)~.}$

Наконец, поскольку ${\displaystyle f\lambda =f'\lambda '=c}$ , то:

${\displaystyle \lambda '-\lambda ={\frac {h}{m_{e}c}}(1-\cos {\theta })~.\qquad \qquad (3)}$

Кроме того, угол ${\displaystyle \varphi }$ между направлением отлетающего электрона и направлением падающего фотона определяется выражением:

${\displaystyle \cot \varphi =\left(1+{\frac {hf}{m_{e}c^{2}}}\right)\tan(\theta /2)~.\qquad \qquad (4)}$

Сечение эффекта Комптона описывается формулой Клейна — Нишины .

Рассеяние на связанном электроне

В случае, если электрон, на котором рассеивается фотон, находится в атоме , то картина рассеяния усложняется.

В случае, если энергия связи электрона больше энергии налетающего фотона, то электрон не выбивается из оболочки , и фотон рассеивается всем атомом как одним целым. В таком случае вместо массы электрона в формуле для изменения длины волны будет стоять масса атома, которая в десятки тысяч раз больше — а значит, и изменение длины волны будет в десятки тысяч раз меньше. Поэтому низкоэнергетические фотоны (например, видимого диапазона ) рассеиваются почти упруго — такое рассеяние называется рэлеевским .

Другим возможным вариантом является рамановское рассеяние , при котором часть энергии фотона переходит в энергию собственных колебаний молекулы или наоборот.

В случае собственно комптоновского рассеяния, если энергия налетающего фотона значительно больше ${\displaystyle {\mathcal {E}}_{0}\gg \alpha Z_{eff}m_{e}c^{2},}$ где ${\displaystyle \alpha }$ — постоянная тонкой структуры, а ${\displaystyle Z_{eff}}$ — эффективный заряд ядра в единицах ${\displaystyle e}$ (разный для разных оболочек), можно считать, что электрон свободен, и его рассеяние описывается формулами рассеяния на свободном электроне .

В случае, если ${\displaystyle m_{e}c^{2}\gg {\mathcal {E}}_{0}\gg E_{3},}$ следует учесть, что в уравнение сохранения энергии при рассеянии добавляется член, связанный с энергией связи, а с другой стороны, проявляется взаимодействие электрона и покинутого им иона . Для описания такого процесса используются фейнмановские диаграммы типа «чайка» .

Вероятность рассеяния близка к нулю при низких энергиях налетающего фотона, она постепенно возрастает при увеличении энергии, а затем спадает. Положение пика зависит от эффективного заряда ядра: чем он больше, тем большей энергии соответствует пик. Также, чем больше значение заряда ядра, тем меньше, в абсолютных величинах, пиковое сечение рассеяния .

В угловом распределении при росте заряда ядра подавляются вылеты с малым углом — то есть, наибольшую вероятность при рассеянии на K-электронах тяжёлых элементов имеет отражение на 180°, даже для высоких энергий .

Ещё одной особенностью рассеяния на электронах в атоме является уширение спектральной линии, соответствующей заданному углу рассеяния. То есть, если при рассеянии на свободном электроне, любому углу соответствует конкретное значение ${\displaystyle \Delta \lambda ,}$ то при рассеянии на атоме каждому углу соответствует целый диапазон таких значений. Это происходит потому, что в атоме электрон локализован, а следовательно имеет неопределенность в импульсе . Ширина линии пропорциональна энергии падающего фотона, и квадратному корню от энергии связи электрона .

Поскольку обычно у атома есть много электронов с разной энергией связи, то при одной и той же энергии падающего фотона для некоторых электронов рассеяние будет происходить по комптоновскому типу, а для других (энергия связи которых больше энергии фотона) — по рэлеевскому, в зависимости от того, с электроном какой оболочки провзаимодействовал фотон. Поэтому реальные спектры рассеянных фотонов обычно содержат два пика — один из них совпадает с частотой падающего света, а второй — с менее энергетическими комптоновскими фотонами .

Комптоновское рассеяние на связанном электроне является основным способом потери энергии в веществе для гамма-квантов среднего диапазона энергий от 100 кэВ (1 МэВ для тяжёлых атомов) до нескольких МэВ. Для фотонов меньшей энергии важнее процессы рэлеевского рассеяния и фотоэффекта , а для более высокоэнергетических — процессы рождения электрон-позитронных пар в кулоновском поле ядра .

Некоторые особые случаи комптоновского рассеяния

Двойное рассеяние

Иногда в процессе рассеяния электрон может поглотить один фотон, а испустить два. Такой процесс происходит значительно реже обычного рассеяния. Наиболее вероятным является случай, когда один из образовавшихся фотонов очень низкоэнергетический, и вероятность излучения двух фотонов с близкими энергиями — минимальная .

Также, возможно излучение трёх и более фотонов, однако оно подавляется с множителем (постоянной тонкой структуры) (1/137) ^n-1, где n — количество фотонов .

При излучении двух и более фотонов теряется прямая зависимость между углом отклонения и изменением длины волны, поэтому правильный учёт шума от двойного комптон-эффекта необходим для точного измерения нормального эффекта Комптона.

Нелинейное рассеяние

В случае, если интенсивность падающего света очень велика, электрон может поглотить несколько фотонов, и испустить один — такой процесс называется нелинейным комптоновским рассеянием. Его сечение, в отличие от обычного рассеяния, зависит от плотности фотонов в пучке . Рассеяние по такому каналу становится вероятным, когда напряжённость поля, создаваемого электромагнитной волной, превышает напряжённость поля в атоме (которая даже для водорода имеет величину около 4·10 ¹⁰ В/м ) более чем в 137 раз. Такие условия возникают при очень высокой интенсивности излучения и на 2020 год являются достижимыми лишь с помощью нескольких самых мощных в мире лазеров (интенсивность излучения которых должна быть выше чем 10 ²¹ Вт/см ). В природе такие процессы могут реализовываться на поверхности нейтронных звёзд .

Рассеяния на тяжёлых частицах

Фотоны могут рассеиваться на протонах и нейтронах так же как на электронах, однако из-за того, что нуклоны почти в 2000 раз тяжелее электрона, изменение длины волны также в тысячи раз меньше, а потому заметным становится лишь для очень высокоэнергетических фотонов . Кроме того, взаимодействие нуклонов в ядре значительно сложнее взаимодействия электрона с ядром, что также влияет на форму спектра рассеянных фотонов .

Применение

Измеряя интенсивность рассеянного света можно с большой точностью определить электронную плотность в теле .

Если объект имеет сложное внутреннее строение, то можно разделить рассеянное излучение, идущее от каждого отдельного участка вдоль луча. Таким образом работает комптоновская томография . Её главным преимуществом является возможность просканировать объект, даже если отсутствует полный доступ к нему (невозможно произвести полный оборот излучателя и детектора), а недостатком — низкое разрешение.

Анализируя сечение комптоновского рассеяния при различных энергиях, можно установить распределение моментов движения электронов в различных оболочках. Зависимость сечения от энергии называется комптоновским профилем вещества . Также знание комптоновского профиля нужно для высокоточной рентгенографии , поскольку комптоновское рассеяние зашумляет картину рентгеновской тени.

Использование эффекта Комптона позволяет создавать лазеры с плавной регулировкой длины волны — такая регулировка происходит вследствие вращения мишени вокруг рассеивателя .

Если фотон детектируется сначала одним детектором, а затем — другим, то, анализируя изменение энергии фотона, можно определить его начальную траекторию . Так работают , имеющие очень широкое поле зрения. Например, телескоп на орбитальной обсерватории «Комптон» имеет поле зрения в 1 стерадиан .

Обратное комптоновское рассеяния релятивистских электронов на реликтовом микроволновом излучении создаёт фотоны отдачи с энергией 50-100 кэВ . Это явление известно как эффект Сюняева — Зельдовича . Детектируя такие высокоэнергетические фотоны, можно изучать крупномасштабное распределение материи во Вселенной . Самый полный обзор источников такого излучения был сделан космическим телескопом «Планк» .

Комптоновское рассеяние

Комптоновское рассеяние имеет первостепенное значение для радиобиологии , поскольку это наиболее вероятное взаимодействие гамма-лучей и рентгеновских лучей высоких энергий с атомами в живых организмах — применяется в лучевой терапии .

В материаловедении комптоновское рассеяние можно использовать для исследования волновой функции электронов в веществе в импульсном представлении .

Комптоновское рассеяние — важный эффект в который приводит к возникновению , поскольку гамма-лучи также рассеиваются за пределы используемых детекторов. используется для обнаружения паразитного рассеяния гамма-лучей, для учёта этого эффекта.

Магнитное комптоновское рассеяние

Магнитное комптоновское рассеяние — это модификация ранее упомянутой техники, которая включает намагничивание кристаллического образца, под действием высокоэнергетических циркулярно-поляризованных фотонов. Путём измерения энергии рассеянных фотонов и изменения намагниченности образца генерируются два разных комптоновских профиля (один для импульсов со спином вверх и один для импульсов со спином вниз). Разница между этими двумя профилями даёт магнитный профиль Комптона (МПК), определяемый функцией ${\displaystyle J_{\text{mag}}(\mathbf {p} _{z})}$ — одномерной проекцией спиновой плотности электронов.

${\displaystyle J_{\text{mag}}(\mathbf {p} _{z})={\frac {1}{\mu }}\iint _{-\infty }^{\infty }(n_{\uparrow }(\mathbf {p})-n_{\downarrow }(\mathbf {p}))d\mathbf {p} _{x}d\mathbf {p} _{y}~,}$

где ${\displaystyle \mu }$ — количество неспаренных электронов в системе;

${\displaystyle n_{\uparrow }(\mathbf {p})}$ и ${\displaystyle n_{\downarrow }(\mathbf {p})}$ представляют собой трёхмерные распределения электронов по импульсам для электронов с основным и неосновным проекциями спина, соответственно.

Поскольку этот процесс рассеяния некогерентен (нет фазового соотношения между рассеянными фотонами), МПК представляет объёмные свойства образца и измеряет основное состояние. Это означает, что МПК идеален для сравнения с теоретическими методами, такими как теория функционала плотности . Площадь под графиком МПК прямо пропорциональна спиновому моменту системы, поэтому в сочетании с методами измерения полного магнитного момента (такими как СКВИД- магнитометрия) может использоваться для выделения как спинового, так и орбитального вкладов в общий магнитный момент системы. Форма МПК также даёт представление о происхождении магнетизма в системе .

Обратный комптоновский эффект

Если фотон рассеивается на движущихся электронах, то энергия рассеянного фотона может быть больше, чем энергия падающего (соответственно, энергия электрона после столкновения уменьшается). Такой процесс называют обратным комптоновским рассеянием. Этот процесс является основным механизмом потери энергии релятивистскими электронами в межзвёздном пространстве. Если начальные скорости фотонов распределены изотропно , то средняя энергия рассеянных фотонов будет равняться :

${\displaystyle {\mathcal {E}}_{1}={\mathcal {E}}_{0}{\frac {4E_{e}}{3m_{e}c^{2}}}~,}$

Энергия рассеянного на электроне фотона:

${\displaystyle {\mathcal {E}}_{1}={\mathcal {E}}_{0}{\frac {1-\beta \cos \theta }{1-\beta \cos(\theta -\phi)+{\frac {{\mathcal {E}}_{0}}{E_{e0}}}(1-\cos \phi)}}~,}$

где: ${\displaystyle \theta }$ — угол между направлениями их движения;

${\displaystyle \phi }$ — угол между направлениями движения падающего и рассеянного фотона;

${\displaystyle \beta =v/c}$ — безразмерная скорость электрона.

В случае «лобового» столкновения :

${\displaystyle {\mathcal {E}}_{1}=E_{e0}{\frac {4{\mathcal {E}}_{0}E_{e0}}{4{\mathcal {E}}_{0}E_{e0}+m^{2}c^{4}}}~.}$

В случае обратного эффекта Комптона изменение длины волны падающего света зависит от его начальной энергии, тогда как для неподвижных электронов такой зависимости нет.

Обратный эффект Комптона ответственен за рентгеновское излучение галактических источников, рентгеновскую составляющую реликтового фонового излучения ( эффект Сюняева — Зельдовича ), трансформацию плазменных волн в высокочастотные электромагнитные волны . Эффект также наблюдается, когда фотоны космического микроволнового фона движутся через горячий газ, окружающий скопление галактик . Фотоны реликтового излучения рассеиваются электронами в этом газе до более высоких энергий, что приводит к эффекту Сюняева — Зельдовича . Наблюдения этого эффекта обеспечивают практически независимые от красного смещения средства обнаружения скоплений галактик.

Обратное комптоновское рассеяние играет важную роль в астрофизике . В рентгеновской астрономии предполагается, что аккреционный диск, окружающий черную дыру , создаёт тепловой спектр. Фотоны с более низкой энергией из этого спектра, рассеиваются до более высоких энергий релятивистскими электронами в окружающей короне . Предполагается, что это вызывает степенну́ю составляющую в рентгеновских спектрах (0,2—10 кэВ) аккреции черных дыр ^{[ источник не указан 927 дней ]} .

Некоторые установки синхротронного излучения рассеивают лазерный свет от ускорительного электронного луча. Это комптоновское обратное рассеяние производит фотоны высоких энергий в диапазоне от МэВ до ГэВ и впоследствии используются в экспериментах по ядерной физике.

Примечания

Литература

• Сивухин Д. В. Атомная физика // . — М. : Наука , 1986. — Т. 5. — 426 с.
• Комптона эффект // / А. М. Прохоров. — М. : Советская энциклопедия , 1990. — Т. 2: Добротность — Магнитооптика. — 703 с.
• Ишханов Б. С., Капитонов И. М., Кэбин Э. И. . — М. : ЛКИ , 2007. — 584 с.