Сферический многогранник или сферическая мозаика — это тa мозаика на сфере , в которой поверхность разделена большими дугами на ограниченные области, называемые сферическими многоугольниками. Большая часть теории симметричных многогранников использует сферические многогранники.

Наиболее известным примером сферического многогранника служит футбольный мяч , который можно понимать как усечённый икосаэдр .

Некоторые «несобственные» многогранники, такие как осоэдры и их двойственные диэдры , существуют только как сферические многогранники и не имеют аналогов с плоскими гранями. В таблице с примерами ниже {2, 6} — осоэдр, а — {6, 2} двойственный ему диэдр.

История

Первые известные сделанные человеком многогранники — это сферические многогранники, высеченные в камне. Многие из них были найдены в Шотландии и датируются периодом Неолита .

Во времена европейских « тёмных столетий » исламский учёный Абуль-Вафа аль-Бузджани написал первую серьёзную работу о сферических многогранниках.

Две сотни лет назад, в начале 19-го века, Пуансо использовал сферические многогранники для обнаружения четырёх правильных звёздчатых многогранников .

В середине 20-го века Коксетер использовал их для перечисления всех (за исключением одного) однородных многогранников , посредством калейдоскопического построения ( Построение Витхоффа ).

Примеры

Все правильные , полуправильные многогранники и их двойственные можно спроектировать на сферу как мозаику. В таблице ниже указаны символы Шлефли {p, q} и схема вершинной фигуры a.b.c. …:

Символ Шлефли	{p, q}	t{p, q}	r{p, q}	t{q, p}	{q, p}	rr{p, q}	tr{p, q}	sr{p, q}
Вершинная фигура	p q	q.2p.2p	p.q.p.q	p. 2q.2q	q p	q.4.p. 4	4.2q.2p	3.3.q.3.p
Тетраэдральные (3 3 2)	3 3	3.6.6	3.3.3.3	3.6.6	3 3	3.4.3.4	4.6.6	3.3.3.3.3
		V3.6.6	V3.3.3.3	V3.6.6		V3.4.4.4	V4.6.6	V3.3.3.3.3
Октаэдральные (4 3 2)	4 3	3.8.8	3.4.3.4	4.6.6	3 4	3.4.4.4	4.6.8	3.3.3.3.4
		V3.8.8	V3.4.3.4	V4.6.6		V3.4.4.4		V3.3.3.3.4
Икосаэдральные (5 3 2)	5 3	3.10.10	3.5.3.5	5.6.6	3 5	3.4.5.4	4.6.10	3.3.3.3.5
		V3.10.10	V3.5.3.5	V5.6.6		V3.4.5.4	V4.6.10
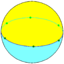
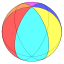
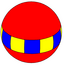
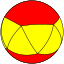
Диэдральные примеры=6 (2 2 6)	6 2	2.12.12	2.6.2.6	6.4.4	2 6	4.6.4		3.3.3.6

Класс	2	3	4	5	6	7	8	10
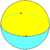
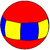
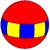
Призма (2 2 p)
Бипирамида (2 2 p)
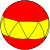
Антипризма
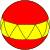
Трапецоэдр

Несобственные случаи

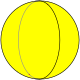
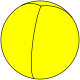
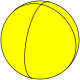
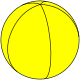
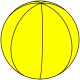
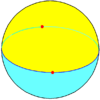
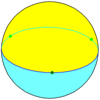
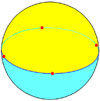
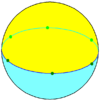
Сферические мозаики допускают случаи, которые невозможны для многогранников, а именно — осоэдры , правильные фигуры {2,n}, и диэдры , правильные фигуры {n,2}.

Семейство правильных осоэдров

Рисунок
Шлефли	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}…
Коксетер
Грани и рёбра	2	3	4	5	6	7	8
Вершины	2

Правильные диэдры: (сферические мозаики)

Рисунок
Шлефли	{2,2}	{3,2}	{4,2}	{5,2}	{6,2}…
Коксетер
Грани	2 {2}	2 {3}	2 {4}	2 {5}	2 {6}
Рёбра и вершины	2	3	4	5	6

Связь с мозаиками на проективной плоскости

Поскольку сфера является двулистным накрытием проективной плоскости, проективные многогранники соответствуют двойному накрытию сферическими многогранниками, имеющими центральную симметрию .

Наиболее известными примерами проективных многогранников служат правильные проективные многогранники, образованные из центрально симметричных правильных многогранников , а также из бесконечных семейств чётных диэдров и осоэдров :

• , {4,3}/2
• , {3,4}/2
• , {5,3}/2
• Полуикосаэдр , {3,5}/2
• Полудиэдр, {2p,2}/2, p>=1
• Полуосоэдр, {2,2p}/2, p>=1

См. также

• Мозаика
• Сферическая геометрия
• Сферическая тригонометрия
• Многогранник
• Тороидальный многогранник
• Нотация Конвея для многогранников

Примечания

Литература