Просто́е число́ — натуральное число , имеющее ровно два различных натуральных делителя . Другими словами, натуральное число ${\displaystyle p}$ является простым, если оно отлично от ${\displaystyle 1}$ и делится без остатка только на ${\displaystyle 1}$ и на само ${\displaystyle p}$ .

Пример: число ${\displaystyle 2}$ простое (делится на ${\displaystyle 1}$ и на ${\displaystyle 2}$ ), а ${\displaystyle 4}$ не является простым, так как, помимо ${\displaystyle 1}$ и ${\displaystyle 4}$ , делится на ${\displaystyle 2}$ — имеет три натуральных делителя.

Изучением свойств простых чисел занимается теория чисел , а основная теорема арифметики устанавливает в ней их центральную роль: любое целое число , превышающее ${\displaystyle 1}$ , либо является простым, либо может быть выражено произведением простых чисел, причём такое представление однозначно с точностью до порядка сомножителей . Единицу не относят к простым числам, так как иначе указанное разложение становится неоднозначным : ${\displaystyle x=1\cdot x=1\cdot 1\cdot x=1\cdot 1\cdot ...\cdot 1\cdot x}$ .

Натуральные числа можно разделить на три класса: единица (имеет один натуральный делитель), простое число (имеет два натуральных делителя), составное число (имеет более двух натуральных делителей) . Как простых, так и составных чисел бесконечно много.

Последовательность простых чисел начинается так:

2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 , 53 , , 61 , , 71 , 73 , 79 , 83 , 89 , 97 , 101 , 103 , 107 , 109 , 113 , 127 , 131 , 137 , 139 , 149 , 151 , , 163 , , 173 , 179 , 181 , , 193 , 197 , 199 , , , , , , 239 , , , 257 , , , , , , 283 , , …

Существуют различные алгоритмы проверки числа на простоту. Например, известный метод перебора делителей , в сравнении с другими примитивный и медленный.

Простые числа широко используются в математике и смежных науках. Во многих алгоритмах информационных технологий , например в асимметричных криптосистемах , используются свойства факторизации целых чисел .

Многие проблемы, касающиеся простых чисел, остаются открытыми .

Существуют обобщения понятия простого числа для произвольных колец и других алгебраических структур .

Множество всех простых чисел обычно обозначают символами ${\displaystyle \mathbf {P} }$ или ${\displaystyle \mathbb {P} }$

История

Неизвестно, когда было определено понятие простого числа, однако первые свидетельства относят к верхнему палеолиту, что подтверждается костью Ишанго .

В сохранившихся записях древнеегипетских математиков есть намёки на то, что у них были некоторые представления о простых числах: например, папирус Райнда , относящийся ко второму тысячелетию до нашей эры, содержит таблицу соотношений числа 2 к ${\displaystyle n}$ , представленных суммой трёх или четырёх египетских дробей с единицей в числителе и различных знаменателях. Разложения дробей, знаменатели которых имеют общий делитель, похожи, поэтому египтяне по крайней мере знали разницу между простыми и составными числами .

Самые ранние дошедшие до нас исследования простых чисел принадлежат математикам Древней Греции . Они изобрели решето Эратосфена — алгоритм последовательного нахождения всех простых чисел от 1 до ${\displaystyle n}$ . Опубликованные в приблизительно трёхсотом году до нашей эры « Начала » Евклида содержат важные теоремы о простых числах, включая бесконечность их множества, лемму Евклида и основную теорему арифметики .

Вплоть до XVII века существенных новых работ в области простых чисел не было . В 1640 году Пьер де Ферма сформулировал малую теорему Ферма , затем доказанную Лейбницем и Эйлером , и теорему о сумме двух квадратов , а также высказал предположение: все числа вида ${\displaystyle 2^{2^{n}}+1}$ являются простыми, и даже доказал это до ${\displaystyle n=4}$ . Но уже для следующего числа Ферма ${\displaystyle 2^{2^{5}}+1}$ Эйлер доказал делимость на ${\displaystyle 641}$ . Новые простые числа в последовательности Ферма не найдены до сих пор. В то же время французский монах Марен Мерсенн обнаружил, что последовательность ${\displaystyle 2^{p}-1}$ , где ${\displaystyle p}$ — простое, даёт также простое число ( числа Мерсенна ).

Работа Эйлера в теории чисел вместила немало сведений о простых. Он показал, что бесконечный числовой ряд ${\displaystyle 1/2+1/3+1/5+1/7+1/11+...}$ — расходящийся. В 1747 году он доказал, что чётные совершенные числа являются значениями последовательности ${\displaystyle 2^{p-1}(2^{p}-1)}$ , где сомножитель является числом Мерсенна. В его переписке с Гольдбахом последний изложил свою знаменитую гипотезу о представлении любого чётного числа, начиная с четырёх, суммой двух простых . Доказательство гипотезы пока не найдено.

С начала XIX века внимание многих математиков занимала проблема асимптотического распределения простых чисел . Лежандр и Гаусс независимо друг от друга высказали предположение: плотность простых чисел в среднем близка к величине, обратно пропорциональной натуральному логарифму .

Долгое время простые числа считались малоприменимыми за пределами чистой математики . Ситуация изменилась в 1970-е годы, после появления концепций криптографии с открытым ключом , в которых простые числа составили основу первых алгоритмов шифрования, таких как RSA .

Разложение натуральных чисел в произведение простых

Представление натурального числа в виде произведения простых называется разложением на простые , или факторизацией числа . На настоящий момент не известны полиномиальные алгоритмы факторизации чисел, хотя и не доказано, что таких алгоритмов не существует. На предполагаемой большой вычислительной сложности задачи факторизации базируется криптосистема RSA и некоторые другие. Факторизация с полиномиальной сложностью теоретически возможна на квантовом компьютере с помощью алгоритма Шора .

Основная теорема арифметики

Основная теорема арифметики утверждает, что каждое натуральное число , большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей . Таким образом, простые числа являются элементарными «строительными блоками» натуральных чисел. Например:

${\displaystyle 23244}$	${\displaystyle =2\cdot 2\cdot 3\cdot 13\cdot 149}$
	${\displaystyle =2^{2}\cdot 3\cdot 13\cdot 149}$ . ( ${\displaystyle 2^{2}}$ обозначает квадратную или вторую степень ${\displaystyle 2}$ .)

Как было показано в этом примере, один и тот же простой делитель может появляться несколько раз. Разложение:

n = p ₁ · p ₂ · ... · p _t

числа n на (конечное число) простых множителей p ₁ , p ₂ , … , p _t называется разложением на простые множители числа n . Основная теорема арифметики может быть перефразирована таким образом: любое разложение на простые числа будет тождественным с точностью до порядка делителей . На практике для большинства чисел есть много простых алгоритмов разложения на множители, все они дают один и тот же результат .

Простота единицы

Большинство древних греков даже не считало ${\displaystyle 1}$ числом, поэтому они не могли считать его простым . К Средним векам и эпохе Возрождения многие математики включали ${\displaystyle 1}$ в качестве первого простого числа . В середине XVIII века Христиан Гольдбах внёс в список ${\displaystyle 1}$ в качестве первого простого числа в своей знаменитой переписке с Леонардом Эйлером ; однако сам Эйлер не считал ${\displaystyle 1}$ простым числом . В XIX веке многие математики по-прежнему считали число ${\displaystyle 1}$ простым числом. Например, список простых чисел Деррика Нормана Лемера до ${\displaystyle 10006721}$ числа, переизданный в 1956 году, начинался с ${\displaystyle 1}$ в качестве первого простого числа. Говорят, что Анри Лебег является последним математиком, который назвал ${\displaystyle 1}$ простым . К началу XX века математики стали приходить к консенсусу о том, что ${\displaystyle 1}$ не является простым числом, а скорее формирует свою специальную категорию — «единицу» .

Если считать ${\displaystyle 1}$ простым числом, то основная теорема Евклида об арифметике (упомянутая выше) не будет выполняться, как было указано в начале статьи. Например, число ${\displaystyle 15}$ может быть разложено как 3 · 5 и 1 · 3 · 5 . Если бы ${\displaystyle 1}$ являлась простым числом, эти два варианта считались бы разными факторизациями ${\displaystyle 15}$ ; следовательно, утверждение этой теоремы пришлось бы изменить . Точно так же решето Эратосфена работало бы неправильно, если бы ${\displaystyle 1}$ считалась простым: модифицированная версия решета, которая предполагает, что ${\displaystyle 1}$ является простым числом, исключает все множители, кратные ${\displaystyle 1}$ (то есть все остальные числа), и даёт на выходе только одно число — ${\displaystyle 1}$ . Кроме того, простые числа имеют несколько свойств, которых нет у числа ${\displaystyle 1}$ , такие как отношение числа к его соответствующему значению функции тождества Эйлера или суммы функции делителей .

Алгоритмы поиска и распознавания простых чисел

Простые способы нахождения начального списка простых чисел вплоть до некоторого значения дают решето Эратосфена , решето Сундарама и решето Аткина .

Однако, на практике вместо получения списка простых чисел зачастую требуется проверить, является ли данное число простым. Алгоритмы, решающие эту задачу, называются тестами простоты . Существует множество полиномиальных тестов простоты, но большинство их является вероятностными (например, тест Миллера — Рабина ) и используются для нужд криптографии . В 2002 году было доказано, что задача проверки на простоту в общем виде полиномиально разрешима, но предложенный детерминированный тест Агравала — Каяла — Саксены имеет довольно большую вычислительную сложность , что затрудняет его практическое применение .

Для некоторых классов чисел существуют специализированные эффективные тесты простоты (см. ниже).

Тест простоты

Тестом простоты (или проверкой простоты) называется алгоритм , который, приняв на входе число, позволяет либо не подтвердить предположение о составности числа, либо точно утверждать его простоту. Во втором случае он называется истинным тестом простоты. Задача теста простоты относится к классу сложности P , то есть время работы алгоритмов её решения зависит от размера входных данных полиномиально, что было доказано в 2002 году . Появление полиномиального алгоритма предсказывалось существованием полиномиальных сертификатов простоты и, как следствие, тем, что задача проверки числа на простоту принадлежала классам NP и co-NP одновременно.

Существующие алгоритмы проверки числа на простоту могут быть разделены на две категории: истинные тесты простоты и вероятностные тесты простоты. Результатом вычислений истинных тестов всегда является факт простоты либо составности числа. Вероятностный тест показывает, является ли число простым с некоторой вероятностью. Числа, удовлетворяющие вероятностному тесту простоты, но являющиеся составными, называются псевдопростыми . Одним из примеров таких чисел являются числа Кармайкла .

Одним из примеров истинных тестов простоты является тест Люка-Лемера для чисел Мерсенна . Очевидный недостаток этого теста заключается в его применимости только к числам определённого вида. Среди других примеров можно привести основанные на малой теореме Ферма

• Тест Пепина для чисел Ферма
• Теорема Прота для чисел Прота
• Тест Агравала — Каяла — Саксены , первый универсальный, полиномиальный, детерминированный и безусловный тест простоты.
• Тест Люка — Лемера — Ризеля

А также:

• метод перебора делителей
• Теорема Вильсона
• Критерий Поклингтона
• Тест Миллера
• Тест Адлемана — Померанса — Румели , усовершенствованный Коэном и Ленстрой
• Тест простоты с использованием эллиптических кривых .

К вероятностным тестам простоты относят:

• Тест Ферма
• Тест Миллера — Рабина
• Тест Соловея — Штрассена
• Тест Бейли — Померанца — Селфриджа — Уогстаффа

Большие простые числа

Уже в течение многих столетий поиск «больших» простых чисел вызывает интерес математиков. В последние десятилетия эти исследования приобрели прикладное значение из-за применения таких чисел в ряде алгоритмов шифрования, таких как RSA .

В семнадцатом столетии Марен Мерсенн предположил, что числа вида ${\displaystyle 2^{n}-1}$ простые (при n ≤ 257) только для n равных 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 и 257 . Проверка верности предположения была намного выше возможностей того времени. Только в XX веке было обнаружено, что гипотеза была ложной и, вероятно, сделана «слепо», поскольку Мерсенн не учел три случая (для n = 61, 89 и 107); кроме того, оказалось, что числа, соответствующие n = 67 и n = 257 — составные .

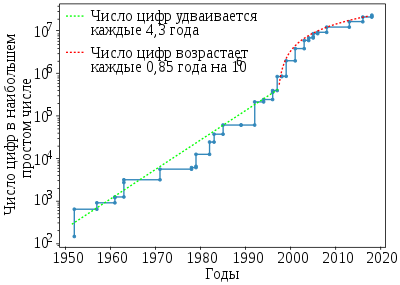
В 1876 году Эдуард Люка доказал, что число M ₁₂₇ (39-значное число) — простое, оно оставалось самым большим известным простым числом до 1951 года, когда были найдены ${\displaystyle {\frac {2^{148}+1}{17}}}$ (44 цифры) и, немного позднее, ${\displaystyle 180*(2^{127}-1)^{2}+1}$ (из 79 цифр) — последнее простое число, которое было найдено с помощью электронного калькулятора. С тех пор все последующие большие простые числа были обнаружены с помощью компьютера: с 1952 года (когда SWAC показал, что M ₅₂₁ является простым), по 1996 год они были найдены суперкомпьютером , и все были простыми Мерсенна (найденные с использованием теста Люка-Лемера , специфического алгоритма для таких чисел), за исключением числа ${\displaystyle 391581*2^{216193}-1}$ , которое было рекордом между 1989 и 1992 годами .

Алгоритмы получения простых чисел

Некоторые задачи математики с использованием факторизации требуют ряд очень больших простых чисел, выбранных случайным образом. Алгоритм их получения, основанный на постулате Бертрана (Для любого натурального n ≥ 2 найдётся простое число p в интервале n < p < 2 n .) :

Алгоритм: Ввод : натуральное число ${\displaystyle N}$ Решение (поиск случайного простого числа P) ${\displaystyle P\gets }$ Функция генерации произвольного натурального числа на отрезке ${\displaystyle [N,2N]}$ Если ${\displaystyle P}$ составное, то ${\displaystyle P\leftarrow \,P+1}$ Если ${\displaystyle P=2N}$ то ${\displaystyle P\leftarrow \,N}$ Возврат « ${\displaystyle P}$ — случайное простое»

Время решения задачи этим алгоритмом не определено, но есть большая вероятность, что оно всегда является полиномиальным, пока имеется достаточно простых чисел, и они распределены более-менее равномерно . Для простых случайных чисел эти условия выполняются .

Наиболее эффективным средством построения простых чисел является несколько модифицированная малая теорема Ферма .

Пусть N, S — нечётные натуральные числа, N-1 = S*R, причем для каждого простого делителя q числа S существует целое число ${\displaystyle a}$ такое, что

${\displaystyle a^{N-1}=1{\pmod {N}}}$ , ${\displaystyle \gcd(a^{{\frac {N-1}{q}}-1},n)=1}$

Тогда каждый простой делитель p числа N удовлетворяет сравнению

${\displaystyle p=1{\pmod {2S}}}$

Следствие. Если выполнены условия теоремы Ферма и ${\displaystyle R\leqslant 4S+2}$ , то N — простое число .

Покажем теперь, как с помощью последнего утверждения, имея большое простое число ${\displaystyle S}$ , можно построить существенно большее простое число ${\displaystyle N}$ . Выберем для этого случайным образом чётное число ${\displaystyle R}$ на промежутке ${\displaystyle R\leqslant 4S+2}$ и положим ${\displaystyle N=SR+1}$ . Затем проверим число ${\displaystyle N}$ на отсутствие малых простых делителей, разделив его на малые простые числа; испытаем ${\displaystyle N}$ некоторое количество раз с помощью алгоритма Рабина. Если при этом выяснится, что ${\displaystyle N}$ — составное число, следует выбрать новое значение ${\displaystyle R}$ и опять повторить вычисления. Так следует делать до тех пор, пока не будет найдено число N, выдержавшее испытание алгоритмом Рабина достаточно много раз. В этом случае появляется надежда на то, что ${\displaystyle N}$ — простое число, и следует попытаться доказать простоту с помощью тестов простоты .

Бесконечность множества простых чисел

Простых чисел бесконечно много. Это утверждение упоминается как теорема Евклида в честь древнегреческого математика Евклида , поскольку первое известное доказательство этого утверждения приписывается ему. Известно ещё много доказательств бесконечности простых чисел, в том числе аналитическое доказательство Эйлера , доказательство Гольдбаха на основе чисел Ферма , доказательство Фурстенберга с использованием общей топологии и элегантное доказательство Куммера .

Наибольшее известное простое

Издавна ведутся записи, отмечающие наибольшие известные на то время простые числа . Один из рекордов поставил в своё время Эйлер , найдя простое число 2 ³¹ − 1 = 2 147 483 647 .

Наибольшим известным простым числом по состоянию на январь 2019 года является число Мерсенна M _{82 589 933} = 2 ^{82 589 933} − 1 . Оно содержит 24 862 048 десятичных цифр ; в книге с записью этого числа было бы около девяти тысяч страниц. Его нашли 7 декабря 2018 года в рамках проекта по распределённому поиску простых чисел Мерсенна GIMPS . Предыдущее самое большое известное простое число, открытое в декабре 2017 года, было на 1 612 623 знака меньше .

Числа Мерсенна выгодно отличаются от остальных наличием эффективного теста простоты : теста Люка — Лемера . Благодаря ему простые числа Мерсенна давно удерживают рекорд как самые большие известные простые.

За нахождение простых чисел из более чем 100 000 000 и 1 000 000 000 десятичных цифр EFF назначила денежные призы соответственно в 150 000 и 250 000 долларов США . Ранее EFF уже присуждала призы за нахождение простых чисел из 1 000 000 и 10 000 000 десятичных цифр.

Простые числа специального вида

Существует ряд чисел, простота которых может быть установлена эффективно с использованием специализированных алгоритмов.

• Числа Мерсенна — числа вида ${\displaystyle M_{n}=2^{n}-1}$ , где n — натуральное число . При этом число Мерсенна может быть простым, только если n — простое число. Как уже было отмечено выше, эффективным тестом простоты является тест Люка — Лемера .
• Числа Ферма — числа вида ${\displaystyle F_{n}=2^{2^{n}}+1}$ , где n — неотрицательное целое число . Эффективным тестом простоты является тест Пепина . По состоянию на февраль 2015 года известно только 5 простых чисел Ферма (для n = 0, 1, 2, 3, 4), двадцать восемь следующих чисел Ферма (до ${\displaystyle F_{32}}$ включительно) оказались составными , однако не доказано, что других простых чисел Ферма нет .
• Числа Вудала — числа вида ${\displaystyle W_{n}=n\cdot 2^{n}-1}$ . Эффективным тестом простоты является тест Люка — Лемера — Ризеля .
• Числа Каллена — числа вида ${\displaystyle C_{n}=n\cdot 2^{n}+1}$ .
• Числа Прота — числа вида ${\displaystyle P=k\cdot 2^{n}+1}$ , причём k нечётно и ${\displaystyle 2^{n}>k}$ . Эффективным тестом простоты для чисел Прота является ( англ. Brillhart–Lehmer–Selfridge test) . Числа Каллена и числа Ферма являются частным случаем чисел Прота (соответственно при k = n и при k = 1, ${\displaystyle n=2^{m}}$ ) .
• Числа Миллса — числа вида ${\displaystyle P_{n}=[A^{3^{n}}],}$ где ${\displaystyle A}$ — константа Миллса .

Для поиска простых чисел обозначенных типов в настоящее время используются проекты распределённых вычислений GIMPS , PrimeGrid , , Seventeen or Bust , , .

Некоторые свойства

• Если p — простое, и p делит ab , то p делит a или b . Доказательство этого факта было дано Евклидом и известно как лемма Евклида . Она используется в доказательстве основной теоремы арифметики .
• Кольцо вычетов ${\displaystyle \mathbb {Z} _{n}}$ является полем тогда и только тогда, когда ${\displaystyle n}$ — простое .
• Характеристика каждого поля — это ноль или простое число .
• Если ${\displaystyle p}$ — простое, а ${\displaystyle a}$ — натуральное, то ${\displaystyle a^{p}-a}$ делится на ${\displaystyle p}$ ( малая теорема Ферма ) .
• Если ${\displaystyle G}$ — конечная группа, порядок которой ${\displaystyle |G|}$ делится на ${\displaystyle p}$ , то ${\displaystyle G}$ содержит элемент порядка ${\displaystyle p}$ ( теорема Коши ) .
• Если ${\displaystyle G}$ — конечная группа, и ${\displaystyle p^{n}}$ — максимальная степень ${\displaystyle p}$ , которая делит ${\displaystyle |G|}$ , то ${\displaystyle G}$ имеет подгруппу порядка ${\displaystyle p^{n}}$ , называемую силовской подгруппой , более того, количество силовских подгрупп равно ${\displaystyle pk+1}$ для некоторого целого ${\displaystyle k}$ ( теоремы Силова ) .
• Натуральное ${\displaystyle p>1}$ является простым тогда и только тогда, когда ${\displaystyle (p-1)!+1}$ делится на ${\displaystyle p}$ ( теорема Вильсона ) .
• Если ${\displaystyle n>1}$ — натуральное, то существует простое ${\displaystyle p}$ , такое, что ${\displaystyle n<p<2n}$ ( постулат Бертрана ) .
• Ряд чисел, обратных к простым , расходится . Более того, при ${\displaystyle x\to \infty }$

  ${\displaystyle \sum _{p<x}{\frac {1}{p}}\ \sim \ \ln \ln x.}$

• Любая арифметическая прогрессия вида ${\displaystyle a,a+q,a+2q,a+3q,...}$ , где ${\displaystyle a,q>1}$ — целые взаимно простые числа , содержит бесконечно много простых чисел ( теорема Дирихле о простых числах в арифметической прогрессии ) .
• Всякое простое число, большее 3, представимо в виде ${\displaystyle 6k+1}$ или ${\displaystyle 6k-1}$ , где ${\displaystyle k}$ — некоторое натуральное число. Отсюда, если разность между несколькими последовательными простыми числами (при k>1) одинакова, то она обязательно кратна 6 — например: 251-257-263-269; 199-211-223; 20183-20201-20219.
• Если ${\displaystyle p>3}$ — простое, то ${\displaystyle p^{2}-1}$ кратно 24 (справедливо также для всех нечётных чисел, не делящихся на 3) .
• Теорема Грина-Тао . Существуют сколь угодно длинные конечные арифметические прогрессии, состоящие из простых чисел .
• Никакое простое число не может иметь вид ${\displaystyle n^{k}-1}$ , где n >2, k >1. Иначе говоря, число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, бо́льшим 2. Из этого следует также, что если простое число имеет вид ${\displaystyle 2^{k}-1}$ , то k — простое (см. числа Мерсенна ) .
• Никакое простое число не может иметь вид ${\displaystyle n^{2k+1}+1}$ , где n >1, k >0. Иначе говоря, число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, бо́льшим 1 .
• Каждое простое число (кроме чисел вида ${\displaystyle 8n-1}$ ) можно представить в виде суммы трех квадратов .

Применения

Простые числа являются фундаментальными компонентами во многих областях математики .

Арифметические функции

Арифметические функции , а именно функции, определённые на множестве натуральных чисел и принимающих значения во множестве комплексных чисел, играют решающую роль в теории чисел. В частности, среди них наиболее важными являются мультипликативные функции, то есть функции ${\displaystyle f}$ , обладающие следующим свойством: если пара ${\displaystyle (a,b)}$ состоит из взаимно простых чисел, то имеет место равенство

${\displaystyle f(ab)=f(a)f(b)}$

Примерами мультипликативных функций являются функция Эйлера ${\displaystyle \phi }$ , которая ставит в соответствие числу ${\displaystyle n}$ количество натуральных чисел, меньших n и взаимно простых с ним и количество делителей числа n . Значение этих функций от степени простого числа:

• Функция ϕ {\displaystyle \phi } Эйлера :

${\displaystyle \phi (p^{m})=p^{m}-p^{m-1}}$

• Функция делителя :

${\displaystyle \sigma (p^{m})=m+1}$

Арифметические функции можно легко вычислить, зная значения, которые они принимают для степеней простых чисел . На самом деле из разложения натурального числа n на множители

${\displaystyle n=p_{1}^{q_{1}}\cdot ...\cdot p_{a}^{q_{a}}}$

мы имеем, что

${\displaystyle f(n)=f(p_{1}^{q_{1}})\cdot ...\cdot f(p_{a}^{q_{a}})}$

и следовательно, возвращаясь к задаче вычисления ${\displaystyle f(n)}$ получается что вычислить ${\displaystyle f}$ от каждой степени простого делителя обычно проще, чем вычислить ${\displaystyle f}$ по общей формуле .

Например, чтобы узнать значение функции Эйлера ${\displaystyle \phi }$ от n = 450 = 2 × 3 ² × 5 ² , достаточно вычислить

${\displaystyle \phi (450)=\phi (2)\cdot \phi (3^{2})\cdot \phi (5^{2})=(2-1)\cdot (9-3)\cdot (25-5)=120}$

Модульная арифметика

В модульной арифметике простые числа играют очень важную роль: кольцо вычетов ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$ является полем тогда и только тогда, когда n является простым . Также существование первообразного корня кольца ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$ привязано к простым числам: оно существует, только если n — простое число, 1, 2, 4 или число в форме ${\displaystyle p^{n}\circ 2p^{n}}$ , где p нечётно.

Одной из важнейших теорем модульной арифметики является малая теорема Ферма . Эта теорема утверждает, что для любого простого числа р и любого натурального числа a имеем:

${\displaystyle a^{p}\equiv a{\pmod {p}}}$

или для любого простого р и любого натурального а не делящегося на р , справедливо:

${\displaystyle a^{p-1}\equiv 1{\pmod {p}}}$

Это свойство можно использовать для проверки того, что число не является простым. На самом деле, если n таково, что:

${\displaystyle a^{n}\not \equiv a{\pmod {n}}}$

для некоторого натурального а , то n не может быть простым . Однако это свойство не может быть использовано для проверки числа на простоту: есть некоторые числа, называемые числами Кармайкла (наименьшее — 561) для которых это будет неверно. Числом Кармайкла называется составное число, которое является псевдопростым числом по каждому основанию b, взаимно простому с n. В 1994 году Уильям Роберт Альфорд, Эндрю Гранвиль и Карл Померанс показали, что таких чисел бесконечно много .

Теория групп

Простые числа также играют основополагающую роль в алгебре . В теории групп группа, в которой каждый элемент является степенью простого числа р , называется р-группой . P-группа является конечной тогда и только тогда, когда порядок группы (число её элементов) является степенью р. Примером бесконечной р-группы является p -группа Прюфера . Известно, что p- группы имеют нетривиальный центр и, следовательно, не могут быть простыми (кроме группы с p элементами); если группа конечна, более того, все нормальные подгруппы пересекают центр нетривиальным образом.

Примером таких групп является циклическая группа умножения по модулю простого числа .

Все группы порядка p являются циклическими и поэтому абелевыми ; также абелева каждая группа порядка p ² . Кроме того, любая конечная абелева группа изоморфна прямому произведению конечного числа циклических р-групп.

В теореме Коши утверждается, что если порядок конечной группы G делится на простое число p, то G содержит элементы порядка p. Эта теорема обобщается теоремами Силова .

Криптосистема с открытым ключом

Некоторые алгоритмы криптографии с открытым ключом, такие как RSA и обмен ключами Диффи-Хеллмана , основаны на больших простых числах (обычно 1024—2048 бит). RSA полагается на предположение, что намного проще (то есть более эффективно) выполнять умножение двух (больших) чисел x и y, чем вычислять взаимно простые x и y , если известно только их произведение ${\displaystyle x\cdot y}$ . Обмен ключами Диффи-Хеллмана основан на том, что существуют эффективные алгоритмы возведения в степень по модулю , а обратная операция — дискретного логарифмирования считается сложной .

RSA

Трудность факторизации больших чисел привела к разработке первого эффективного метода криптографии с открытым ключом — RSA . В этой криптографической системе, человек, который должен получить зашифрованное сообщение, генерирует ключ: выбираются два различных случайных простых числа ${\displaystyle p}$ и ${\displaystyle q}$ заданного размера (обычно используются, 1024- или 2048- битные числа). Далее вычисляется их произведение ${\displaystyle n=p*q}$ , называемое модулем . Вычисляется значение функции Эйлера от числа ${\displaystyle n}$ : ${\displaystyle \phi (n)=(p-1)(q-1)}$ . Выбирается целое число ${\displaystyle e}$ ( ${\displaystyle 1<e<\phi (n)}$ ), взаимно простое со значением функции ${\displaystyle \phi (n)}$ . Обычно в качестве ${\displaystyle e}$ берут небольшие простые числа (например, простые числа Ферма ). Число ${\displaystyle e}$ называется открытой экспонентой ( англ. public exponent). Вычисляется число ${\displaystyle d}$ , называемое секретной экспонентой, мультипликативно обратное к числу e по модулю ${\displaystyle \phi (n)}$ . Пара ${\displaystyle \{e,n\}}$ публикуется в качестве открытого ключа RSA ( англ. RSA public key). Пара ${\displaystyle \{d,\phi (n)\}}$ играет роль закрытого ключа RSA ( англ. RSA private key) и держится в секрете .

Теоретически можно получить закрытый ключ из общедоступной информации: в настоящее время для этого требуется факторизация числа ${\displaystyle n}$ , что делает передачу защищенного сообщения безопасной, если простые числа удовлетворяют определённым условиям и являются «достаточно большими». Пока не известно, существуют ли эффективные методы для расшифровки сообщения, не связанные с прямой атакой на факторизацию ${\displaystyle n}$ , но было показано, что плохой выбор открытого ключа может сделать систему более уязвимой для таких атак .

В 1991 году опубликовала список полупростых чисел, предлагая денежные призы за разложение некоторых из них на множители, с целью подтверждения безопасности метода и поощрения исследования в этой области: инициатива называлась . На протяжении многих лет некоторые из этих чисел были разложены, а для других проблема факторизации все ещё остается открытой; однако конкурс был завершен в 2007 году .

Формулы для нахождения простых чисел

В разное время предпринимались попытки указать выражение, значениями которого при разных значениях входящих в него переменных были бы простые числа . Л. Эйлер указал многочлен ${\displaystyle \textstyle n^{2}-n+41,}$ принимающий простые значения при n = 0, 1, 2, …, 40 . Однако при n = 41 значение многочлена является составным числом. Можно доказать, что не существует многочлена от одной переменной n , который принимает простые значения при всех целых n . П. Ферма предположил, что все числа вида 2 2 k + 1 простые; однако Эйлер опроверг эту гипотезу, доказав, что число 2 ^{2 5} + 1 = 4 294 967 297 — составное .

Тем не менее, существуют многочлены, множество положительных значений которых при неотрицательных значениях переменных совпадает с множеством простых чисел. Одним из примеров является многочлен

${\displaystyle {\begin{aligned}{\bigl (}k+2{\bigr)}{\bigl \{}1&-{\bigl [}wz+h+j-q{\bigr ]}^{2}-{\bigl [}(gk+2g+k+1)(h+j)+h-z{\bigr ]}^{2}-{\bigl [}2n+p+q+z-e{\bigr ]}^{2}\\&-{\bigl [}16(k+1)^{3}(k+2)(n+1)^{2}+1-f^{2}{\bigr ]}^{2}-{\bigl [}e^{3}(e+2)(a+1)^{2}+1-o^{2}{\bigr ]}^{2}-{\bigl [}(a^{2}-1)y^{2}+1-x^{2}{\bigr ]}^{2}\\&-{\bigl [}16r^{2}y^{4}(a^{2}-1)+1-u^{2}{\bigr ]}^{2}-{\bigl [}((a+u^{2}(u^{2}-a))^{2}-1)(n+4dy)^{2}+1-(x+cu)^{2}{\bigr ]}^{2}-{\bigl [}n+l+v-y{\bigr ]}^{2}\\&-{\bigl [}(a^{2}-1)l^{2}+1-m^{2}{\bigr ]}^{2}-{\bigl [}ai+k+1-l-i{\bigr ]}^{2}-{\bigl [}p+l(a-n-1)+b(2an+2a-n^{2}-2n-2)-m{\bigr ]}^{2}\\&-{\bigl [}q+y(a-p-1)+s(2ap+2a-p^{2}-2p-2)-x{\bigr ]}^{2}-{\bigl [}z+pl(a-p)+t(2ap-p^{2}-1)-pm{\bigr ]}^{2}{\bigr \}}\end{aligned}}}$

содержащий 26 переменных и имеющий степень 25. Наименьшая степень для известных многочленов такого типа — 5 при 42 переменных; наименьшее число переменных — 10 при степени около 1,6·10 ⁴⁵ . Этот результат является частным случаем доказанной Юрием Матиясевичем диофантовости любого перечислимого множества .

Интересно, что приведённый выше многочлен, который порождает простые числа, сам разлагается на множители. Заметим, что второй множитель этого многочлена (в фигурных скобках) имеет форму: единица минус сумма квадратов. Таким образом, многочлен может принимать положительные значения (при положительных ${\displaystyle k}$ ) только если, каждый из этих квадратов (то есть каждый многочлен в квадратных скобках) равен нулю. В этом случае выражение в фигурных скобках будет равно 1 .

Открытые вопросы

До сих пор существует много открытых вопросов относительно простых чисел, наиболее известные из которых были перечислены Эдмундом Ландау в 1912 году на Пятом Международном математическом конгрессе :

1. Проблема Гольдбаха ( первая проблема Ландау ): верно ли, что каждое чётное число, большее двух, может быть представлено в виде суммы двух простых чисел?
2. Вторая проблема Ландау : бесконечно ли множество « простых близнецов » — пар простых чисел, разность между которыми равна 2 ? В 2013 году математик Чжан Итан из университета Нью-Гэмпшира доказал, что существует бесконечно большое количество пар простых чисел, расстояние между которыми не превышает 70 миллионов . Другими словами, всегда будут встречаться простые числа, удалённые друг от друга не более чем на 70 млн. Уже 20 июля 2013 года усилиями удалось снизить оценку расстояния до 4680 . В ноябре того же года Джеймс Мэйнард улучшил результат до 600 . Используя идеи Мэйнарда в 2014 году проект Polymath под руководством Теренса Тао несколько улучшили последний метод, гарантируя бесконечное число пар простых чисел с расстоянием не более 246 .
3. Гипотеза Лежандра ( третья проблема Ландау ): верно ли, что для всякого натурального числа ${\displaystyle n}$ между ${\displaystyle n^{2}}$ и ${\displaystyle (n+1)^{2}}$ всегда найдётся простое число ?
4. Четвёртая проблема Ландау : бесконечно ли множество простых чисел вида ${\displaystyle n^{2}+1}$ , где ${\displaystyle n}$ — натуральное число ?

Открытой проблемой является также существование бесконечного количества простых чисел во многих целочисленных последовательностях, включая числа Мерсенна , числа Фибоначчи , числа Ферма и др.

Вариации и обобщения

Неприводимые и простые элементы

В начале статьи было дано определение простого числа: натуральное число называется простым, если у него ровно два делителя — единица и само число. Аналогичное понятие можно ввести и в других алгебраических структурах; чаще всего рассматривается коммутативные кольца без делителей нуля ( области целостности ) . У таких колец, однако, могут быть делители единицы , образующие мультипликативную группу . Например, в кольце целых чисел существуют два делителя единицы: ${\displaystyle +1}$ и ${\displaystyle -1.}$ Поэтому все целые числа, кроме делителей единицы, имеют не два, а по меньшей мере четыре делителя; например, у числа 7 делителями являются ${\displaystyle 1;7;-1;-7.}$ Это означает, что обобщение понятия простого числа должно опираться на иные его свойства.

Аналогом простого числа для области целостности является неприводимый элемент , который определяется следующим образом .

Ненулевой элемент ${\displaystyle p}$ области целостности называется неприводимым (иногда неразложимым ), если он не является делителем единицы и из равенства ${\displaystyle p=ab}$ следует, что ${\displaystyle a}$ или ${\displaystyle b}$ является делителем единицы.

Для целых чисел это определение означает, что неприводимыми элементами являются простые натуральные числа, а также противоположные им.

Из определения следует, что множество делителей неприводимого элемента ${\displaystyle p}$ состоит из двух частей: все делители единицы и произведения ${\displaystyle p}$ на все делители единицы (эти произведения называются элементами, ассоциированными с ${\displaystyle p}$ ). То есть количество делителей неприводимого ${\displaystyle p,}$ если оно конечно, вдвое больше количества делителей единицы в кольце.

Важное значение имеет аналог основной теоремы арифметики , который в обобщённом виде формулируется следующим образом :

Кольцо называется факториальным , если в нём каждый ненулевой элемент, не являющийся делителем единицы, может быть представлен в виде произведения неприводимых элементов, причём это представление единственно с точностью до перестановки сомножителей и их ассоциированности (умножения на делители единицы).

Не всякая область целостности факториальна, см. контрпример . Евклидово кольцо всегда факториально .

Существует другое, более узкое обобщение понятия простого числа, называемое простым элементом .

Ненулевой элемент ${\displaystyle p}$ области целостности называется простым , если он не является делителем единицы и произведение ${\displaystyle ab}$ может делиться на ${\displaystyle p}$ лишь в том случае, когда хотя бы один из элементов ${\displaystyle a}$ или ${\displaystyle b}$ делится на ${\displaystyle p}$ .

Простой элемент всегда неприводим. В самом деле, если элемент ${\displaystyle p}$ простой и ${\displaystyle p=ab,}$ то по определению простого элемента один из сомножителей, пусть это будет ${\displaystyle a,}$ делится на ${\displaystyle p,}$ то есть ${\displaystyle a=pq.}$ Тогда ${\displaystyle p=ab=pqb}$ или, сокращая на ${\displaystyle p}$ (в области целостности сокращение ненулевого множителя всегда возможно): ${\displaystyle 1=qb,}$ то есть ${\displaystyle b}$ является делителем единицы. ■

Обратное, вообще говоря, неверно, неприводимый элемент может не быть простым, если кольцо не является факториальным. Пример : рассмотрим кольцо чисел вида ${\displaystyle a+b{\sqrt {5}}i,}$ где ${\displaystyle a,b}$ — целые числа. Число 3 в нём неприводимо, так как у него только 4 делителя: ${\displaystyle 3,1,-3,-1}$ . Однако оно не является простым элементом, в чём убеждает равенство:

${\displaystyle \left(2+{\sqrt {5}}i\right)\left(2-{\sqrt {5}}i\right)=9}$

Число 3 делит правую часть равенства, но не делит ни одного из сомножителей. Можно из этого факта сделать вывод, что рассмотренное кольцо не факториально; и в самом деле, равенство ${\displaystyle 6=2\cdot 3=(1-i{\sqrt {5}})(1+i{\sqrt {5}})}$ показывает, что разложение на неприводимые множители в этом кольце не однозначно.

Примеры

Кольцо целых чисел факториально. В нём, как уже упоминалось выше, два делителя единицы.

Гауссовы целые числа

Кольцо гауссовых чисел состоит из комплексных чисел вида ${\displaystyle a+bi,}$ где ${\displaystyle a,b}$ — целые числа. Делителей единицы четыре: ${\displaystyle 1;-1;i;-i.}$ Это кольцо факториально, неприводимыми элементами являются часть обычных простых чисел и «простые гауссовы» (например, ${\displaystyle 1+i}$ ). См. критерий простоты гауссова числа .

Пример разложения для числа 2, которое в кольце гауссовых чисел не является простым: ${\displaystyle 2=(1+i)(1-i)=i(1-i)(1-i)}$ — неединственность разложения здесь кажущаяся, поскольку ${\displaystyle 1-i}$ ассоциирована с ${\displaystyle 1+i}$ , согласно равенству: ${\displaystyle 1-i=(-i)(1+i).}$

Целые числа Эйзенштейна

Кольцо целых чисел Эйзенштейна ${\displaystyle \mathbb {Z} [\omega ]}$ состоит из комплексных чисел следующего вида :

${\displaystyle z=a+b\omega ,}$ где ${\displaystyle a,b}$ — целые числа, ${\displaystyle \omega ={\frac {1}{2}}(-1+i{\sqrt {3}})=e^{2\pi i/3}}$ ( кубический корень из единицы ),

В этом кольце шесть делителей единицы: (±1, ±ω, ±ω ² ), оно евклидово и поэтому факториально. Неприводимые элементы (они же простые элементы) кольца называются простыми числами Эйзенштейна.

Критерий простоты : целое число Эйзенштейна ${\displaystyle z=a+b\omega }$ является простым числом Эйзенштейна тогда и только тогда, когда выполняется одно из следующих взаимоисключающих условий:

1. ${\displaystyle z}$ ассоциировано с натуральным простым числом вида ${\displaystyle 3n-1.}$
2. ${\displaystyle |z|^{2}=a^{2}-ab+b^{2}}$ (норма ${\displaystyle z}$ ) является натуральным простым вида ${\displaystyle 3n}$ или ${\displaystyle 3n+1}$ .

Отсюда следует, что норма любого целого числа Эйзенштейна является либо простым натуральным числом, либо квадратом простого натурального числа .

Числа, ассоциированные или комплексно-сопряжённые с простыми числами Эйзенштейна, также являются простыми числами Эйзенштейна.

Кольцо многочленов

Большое значение в алгебре имеет кольцо многочленов ${\displaystyle K[x]}$ , образованное многочленами с коэффициентами из некоторого поля ${\displaystyle K.}$ Делителями единицы являются здесь ненулевые константы (как многочлены нулевой степени). Кольцо многочленов евклидово и поэтому факториально. Если в качестве ${\displaystyle K}$ взять поле вещественных чисел , то неприводимыми будут все многочлены 1-й степени и те многочлены 2-й степени, у которых нет вещественных корней (то есть их дискриминант отрицателен) .

См. также

Примечания

Литература

• Ван дер Варден . Алгебра. Определения, теоремы, формулы. — СПб. : Лань, 2004. — 624 с. — ISBN 5-8114-0552-9 .
• Василенко О. Н. . — М. : МЦНМО , 2003. — 328 с. — ISBN 5-94057-103-4 . от 27 января 2007 на Wayback Machine
• Винберг Э. Б. // Математическое просвещение — М. : Изд-во МЦНМО , 2008. — Т. 12. — С. 43—53.
• Гальперин Г. // Квант . — № 4 . — С. 9—14,38 .
• Генри С. Уоррен, мл. Глава 16. Формулы для простых чисел // Алгоритмические трюки для программистов = Hacker's Delight. — М. : «Вильямс», 2007. — 288 с. — ISBN 0-201-91465-4 .
• Карпушина Н. (рус.) // Наука и жизнь . — 2010. — № 5 .
• Кордемский Б. А. . — М. : ГИФМЛ, 1958. — 576 с.
• Кормен Т., Лейзер Ч. Глава 33.8. Проверка чисел на простоту // . — М. : МЦНМО, 2002. — С. 765—772. — ISBN 5-900916-37-5 .
• Крэндалл Р. , Померанс К. Простые числа. Криптографические и вычислительные аспекты = Prime Numbers: A Computational Perspective. — М. : УРСС , Либроком, 2011. — 664 с. — ISBN 978-5-397-02060-2 .
• Курош А. Г. Лекции по общей алгебре. — 2-е изд.. — Наука, 1973.
• Ленг С. Алгебра. — М. : Мир, 1967.
• Матиясевич Ю. . // Квант . — 1975. — № 5 . — С. 5—13 .
• Нестеренко Ю. В. // / Под редакцией В. В. Ященко. — Питер, 2001. — 288 с. — ISBN 5-318-00443-1 .
• Цагер Д. (рус.) // Успехи математических наук . — Российская академия наук , 1984. — Т. 39 , № 6(240) . — С. 175—190 .
• Черёмушкин А. В. . — М. : МЦНМО , 2002. — 104 с. — 2000 экз. — ISBN 5-94057-060-7 . 31 мая 2013 года. .
• Простое число // / Сост. А. П. Савин. — М. : Педагогика , 1985. — С. —263. — 352 с.
• Энрике Грасиан . Простые числа. Долгая дорога к бесконечности. — Де Агостини, 2014. — Т. 3. — 148 с. — (Мир математики). — ISBN 978-5-9774-0682-6 . — ISBN 978-5-9774-0637-6 .
• , (англ.) // — 2012. — Vol. 9, Iss. 1, No 3. — P. 175—178. — ISSN ;
• Crandall R., Pomerance C. Глава 3. «Recognizing Primes and Composites». Глава 4. «Primality Proving» // . — Springer, 2005. — С. 117—224. — ISBN 0-387-25282-7 .

Ссылки

• Кноп К. .
• (англ.) — база данных наибольших известных простых чисел (англ.) .
• (исп.) .
• (англ.) .