Interested Article - Правильный косой многогранник

Правильный косой многогранник — это обобщение множества правильных многогранников , которое включает возможность непланарных граней или вершинных фигур . Коксетер рассматривал косые вершинные фигуры, которые создавали новые четырёхмерные правильные многогранники, а много позднее Бранко Грюнбаум рассматривал правильные косые грани.

Описание правильных косых многогранников

Правильные косые многогранники не являются многогранниками в привычном смысле. Как Коксетер пишет в статье THE REGULAR SPONGES, OR SKEW POLYHEDRA (Правильные губки или косые многогранники), «Заполнение гранями отличается от конечных многогранников тем, что для них понятия внутри и снаружи совершено одно и то же. Такие заполнения помогают думать о многограннике как о поверхности, а не как о теле. Чтобы получить новые многогранники, нужно изловчиться, чтобы у вершины можно было разместить больше многоугольников, чем это разрешается кристаллографическими ограничениями (сумма углов при вершине меньше $2\pi$ $2\pi$ )». Чтобы достичь такого эффекта, Петри разрешил рёбрам идти в другую сторону от плоскости, что приводит к губкам , то есть поверхностям с незакрытыми дырами (дыра одного многогранника закрывается дырой другого, так что все они образуют бесконечную губку ) .

История

Согласно Коксетеру в 1926 обобщил концепцию пространственных многоугольников (непланарных многоугольников) в правильные косые многогранники .

Коксетер предложил модифицированный символ Шлефли {l,m|n} для этих фигур, где {l,m} означает вершинную фигуру , m l-угольников вокруг вершины, а n — n -угольные дыры. Их вершинные фигуры являются пространственными многоугольниками , пробегающими зигзагом между двумя плоскостями.

Правильные косые многогранники, представленные символом {l,m|n}, удовлетворяют равенству:

2*cos(π/l)*cos(π/m)=cos(π/n)

Первое множество {l, m | n} представляет пять выпуклых платоновых тел и одно невыпуклое тело Кеплера — Пуансо :

{l, m \| n}	Граней	Рёбер	Вершин	p	Многогранник	Порядок симметрии
{3,3\| 3} = {3,3}	4	6	4	0	Тетраэдр	12
{3,4\| 4} = {3,4}	8	12	6	0	Октаэдр	24
{4,3\| 4} = {4,3}	6	12	8	0	Куб	24
{3,5\| 5} = {3,5}	20	30	12	0	Икосаэдр	60
{5,3\| 5} = {5,3}	12	30	20	0	Додекаэдр	60
{5,5\| 3} = {5,5/2}	12	30	12	4	Большой додекаэдр	60

Конечные правильные косые многогранники в 4–мерном пространстве

A4 проекции плоскости Коксетера

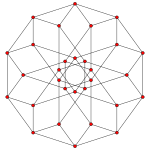
{4, 6 \| 3}	{6, 4 \| 3}
(60 рёбер, 20 вершин)	(60 рёбер, 30 вершин)
F4 проекции плоскости Коксетера

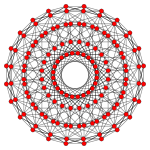
{4, 8 \| 3}	{8, 4 \| 3}
(576 рёбер, 144 вершин)	(576 рёбер, 288 вершин)
Некоторые из 4-мерных правильных косых многогранников укладываются в однородные многогранники, как показано на проекциях.

Коксетер также перечислил большое число конечных правильных многогранников в своей статье "regular skew polyhedra in three and four dimensions, and their topological analogues" (правильные косые многогранники в трёхмерном и четырёхмерном пространствах и их топологические аналоги).

Подобно как бесконечные косые многогранники представляют поверхность многообразия между ячейками , конечные виды представляют поверхности многообразия в ячейках .

Многогранники вида {2p, 2q | r} связаны с группой Коксетера симметрии [(p,r,q,r)], которая сводится к линейной [r,p,r] при q, равном 2. Коксетер даёт этой симметрии обозначение [[( p , r , q , r )] ⁺ ], которая, по его словам, изоморфна его абстрактной группе (2 p ,2 q |2, r ). Связанные соты имеют расширенную симметрию [[( p , r , q , r ) ]] .

{2p,4|r} представляется {2p} гранями {r,p,r} , а {4,2p|r} представляется квадратными гранями {r,p,r} (рансифицировнного).

{4,4|n} образует n - n дуопризму , и, в частности, {4,4|4} укладывается в {4}x{4} тессеракт .


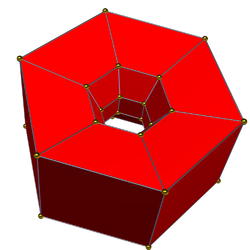
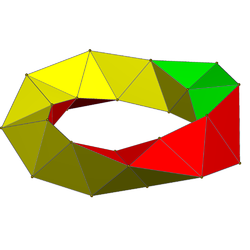
{4,4\| n} представляют квадратные грани дуопризм, с n-угольными гранями в качестве дыр и представляет тор Клиффорда и аппроксимацию	{4,4\|6} имеет 36 квадратных граней и в перспективной проекции выглядит как квадраты, выбранные в 6,6 .	Кольцо из 60 треугольников образует правильный косой многогранник в подмножестве граней 600-ячейника .

Чётные упорядоченные решения
{l, m \| n}	Граней	Рёбер	Вершин	p	Структура		Порядок	Связанный
{4,4\| 3}	9	18	9	1	D ₃ xD ₃	[[3,2,3] ⁺ ]	9	3-3 дуопризма
{4,4\| 4}	16	32	16	1	D ₄ xD ₄	[[4,2,4] ⁺ ]	16	4-4 дуопризма или тессеракт
{4,4\| 5}	25	50	25	1	D ₅ xD ₅	[[5,2,5] ⁺ ]	25	5-5 дуопризма
{4,4\| 6}	36	72	36	1	D ₆ xD ₆	[[6,2,6] ⁺ ]	36	6-6 дуопризма
{4,4\| n}	n ²	2n ²	n ²	1	D _n xD _n	[[n,2,n] ⁺ ]	n ²	n-n дуопризма
{4,6\| 3}	30	60	20	6	S5	[[3,3,3] ⁺ ]	60
{6,4\| 3}	20	60	30	6	S5	[[3,3,3] ⁺ ]	60
{4,8\| 3}	288	576	144	73		[[3,4,3] ⁺ ]	576
{8,4\| 3}	144	576	288	73		[[3,4,3] ⁺ ]	576

Пентаграммные решения
{l, m \| n}	Граней	Рёбер	Вершин	p	Структура		Порядок	Связанный
{4,5\| 5}	90	180	72	10	A6	[[5/2,5,5/2] ⁺ ]	360	Струганый
{5,4\| 5}	72	180	90	10	A6	[[5/2,5,5/2] ⁺ ]	360	Глубокоусечённый

{l, m \| n}	Граней	Рёбер	Вершин	p	Структура	Порядок
{4,5\| 4}	40	80	32	5	?	160
{5,4\| 4}	32	80	40	5	?	160
{4,7\| 3}	42	84	24	10	LF(2,7)	168
{7,4\| 3}	24	84	42	10	LF(2,7)	168
{5,5\| 4}	72	180	72	19	A6	360
{6,7\| 3}	182	546	156	105	LF(2,13)	1092
{7,6\| 3}	156	546	182	105	LF(2,13)	1092
{7,7\| 3}	156	546	156	118	LF(2,13)	1092
{4,9\| 3}	612	1224	272	171	LF(2,17)	2448
{9,4\| 3}	272	1224	612	171	LF(2,17)	2448
{7,8\| 3}	1536	5376	1344	1249	?	10752
{8,7\| 3}	1344	5376	1536	1249	?	10752

Последнее множество основано на дальнейших расширенных форм Коксетера {q1,m|q2,q3...} или с q2 неспецифицированным: {l, m |, q}.

{l, m \|, q}	Граней	Рёбер	Вершин	p	Структура	Порядок
{3,6\|,q}	2q ²	3q ²	q ²	1	?	2q ²
{3,2q\|,3}	2q ²	3q ²	3q	(q-1)*(q-2)/2	?	2q ²
{3,7\|,4}	56	84	24	3	LF(2,7)	168
{3,8\|,4}	112	168	42	8	PGL(2,7)	336
{4,6\|,3}	84	168	56	15	PGL(2,7)	336
{3,7\|,6}	364	546	156	14	LF(2,13)	1092
{3,7\|,7}	364	546	156	14	LF(2,13)	1092
{3,8\|,5}	720	1080	270	46	?	2160
{3,10\|,4}	720	1080	216	73	?	2160
{4,6\|,2}	12	24	8	3	S4 ×S2	48
{5,6\|,2}	24	60	20	9	A5 ×S2	120
{3,11\|,4}	2024	3036	552	231	LF(2,23)	6072
{3,7\|,8}	3584	5376	1536	129	?	10752
{3,9\|,5}	12180	18270	4060	1016	LF(2,29)×A3	36540

См. также

Пространственный многоугольник

Примечания

, p. 7, 17.
, с. 20-22.
В английской литературе — skew polygon, буквально — косой многоугольник . В русской литературе прижился термин пространственный многоугольник , а термин косой многоугольник соответствует термину skew polyhedron ( косой многогранник ). В данной статье используются оба термина косой многоугольник и косой многогранник как синонимы.
.

Литература

Peter McMullen. Four-Dimensional Regular Polyhedra // Discrete & Computational Geometry September. — 2007. — Т. 38 , вып. 2 . — С. 355-387 .
H. S. M. Coxeter . Regular Polytopes. — 3rd. — Dover Publications, Inc., 1973. . См., в частности, таблицы I и II: Regular polytopes and honeycombs, стр. 294–296.
H. S. M. Coxeter . — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6 . от 11 июля 2016 на Wayback Machine
- (Paper 2) H.S.M. Coxeter, "The Regular Sponges, or Skew Polyhedra", 6 (1939) 240-244.
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- H.S.M. Coxeter. Regular and Semi-Regular Polytopes II // Math. Zeit. — 1985. — Вып. 188 . — С. 559–591 .
H.S.M. Coxeter . Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — ISBN 978-0486-40919-8 .
- H. S. M. Coxeter. Regular Skew Polyhedra in Three and Four Dimensions. // Proc. London Math. Soc.. — 1937. — Т. 43 . — С. 33-62 .
C. W. L. Garner. // Canad. J. Math.. — 1967. — Т. 19 . — С. 1179-1186 .
E. Schulte, J.M. Wills. On Coxeter's regular skew polyhedral // Discrete Mathematics. — 1986. — Т. 60, June–July . — С. 253–262 .
Peter McMullen, Egon Schulte. Abstract Regular Polytopes. — Cambridge University Press, 2002. — Т. 92. — (Encyclopedia of Mathematics and its Applications). — ISBN 0-521-81496-0 . — doi : .