Interested Article - Полигекс

- 2020-03-23
- 1
Полигекс ( англ. polyhex) , или шестиугольный монстр ( англ. hexagonal animal) — геометрическая фигура в виде многоугольника , составленного из нескольких правильных шестиугольников , соединённых сторонами. Полигексы можно рассматривать как конечные подмножества шестиугольного паркетажа со связной внутренностью.
Наряду с другими полиформами — полимино и полиамондами , полигексы широко используются в занимательной математике, в основном в задачах на составление фигур. Название предложено по аналогии с названиями других полиформ .
По форме полигексы напоминают структурные формулы полициклических ароматических углеводородов (каждый шестиугольник соответствует бензольному кольцу ).
Число полигексов
Как и в случае полимино , различают «свободные» полигексы (когда повороты и отражения считаются такой же фигурой), «односторонние», когда фигуры при зеркальных отражениях считаются различными, и «фиксированные», различаемые также и при поворотах.
Число «свободных» n -гексов для n = 1, 2, 3, 4… даётся последовательностью
Другие последовательности OEIS, связанные с полигексами:
- число полигексов с отверстиями — ;
- число полигексов без отверстий — ;
- число фиксированных полигексов — ;
- число односторонних полигексов — .
| Моногекс |
|
| Дигекс |
|
| Три тригекса |
|
| Семь тетрагексов |
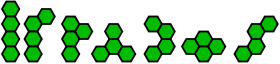
|
| 22 пентагекса |

|
| 82 гексагекса |
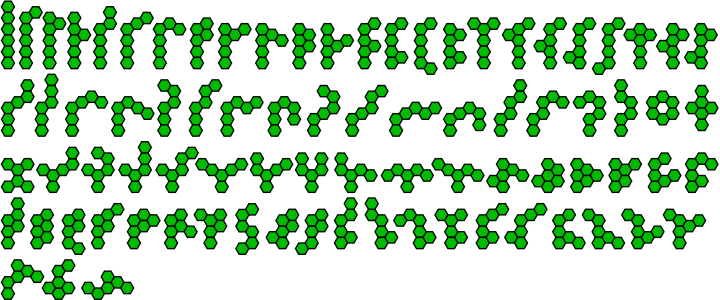
|
См. также
Примечания
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- ↑ Гарднер М. . Математические новеллы / Пер. с англ. Ю. А. Данилова. Под ред. Я. А. Смородинского.. — М. : Мир, 1974. — С. 267 — 281.
- Голомб С.В. . = Polyominoes / Пер. с англ. В. Фирсова. Предисл. и ред. И. Яглома . — М. : Мир, 1975. — С. — 147. — 207 с.
- George E. Martin. Polyominoes: a guide to puzzles and problems in tiling (англ.) . — MAA , 1996. — ISBN 0-88385-501-1 . The Animals.
Ссылки
- Библиотека по математике от 20 августа 2013 на Wayback Machine
- 2020-03-23
- 1