Ли́нза ( нем. Linse , от лат. lens — чечевица) — деталь из прозрачного однородного материала , имеющая две преломляющие полированные поверхности, например, обе сферические или же одну плоскую, а другую — сферическую. В настоящее время всё чаще применяются и «асферические линзы» , форма поверхности которых отличается от сферы. В качестве материала линз обычно используются оптические материалы , такие как стекло , оптическое стекло , кристаллы , оптически прозрачные пластмассы и другие материалы .

Термин «линза» используют также применительно к другим приборам и явлениям, действие которых на излучение подобно действию линзы, например:

• плоские «линзы», изготовленные из материала с переменным показателем преломления , изменяющимся в зависимости от расстояния от центра;
• линзы Френеля ;
• зонная пластинка Френеля , использующая явление дифракции ;
• «линзы» воздуха в атмосфере — неоднородность свойств, в частности показателя преломления (проявляется в виде мерцания изображения звёзд в ночном небе);
• гравитационная линза — наблюдаемый на межгалактических расстояниях эффект отклонения электромагнитных волн массивными объектами;
• магнитная линза — устройство, использующее постоянное магнитное поле для фокусирования пучка заряженных частиц ( ионов или электронов ) и применяющееся в электронных и ионных микроскопах ;
• изображение линзы, сформированное оптической системой или частью оптической системы. Используется при расчёте сложных оптических систем.

История

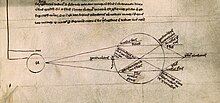
Слово происходит от lēns , латинского названия чечевицы , потому что двояковыпуклая линза имеет форму чечевицы. Линзой также называется .

Некоторые учёные утверждают, что археологические свидетельства указывают на широкое использование линз в древности на протяжении нескольких тысячелетий . Так называемая линза Нимруда — артефакт из горного хрусталя , датируемый VIII веком ( 750 — 710 гг.) до нашей эры, который, возможно, использовался в качестве увеличительного или зажигательного стекла либо предназначался для других целей . Другие предположили, что некоторые египетские иероглифы изображают «простые стеклянные менисковые линзы» .

Самый древний литературный источник, в котором упоминается об использовании линз, а именно зажигательного стекла, — пьеса Аристофана « Облака » (424 г. до н. э.) . Плиний Старший (I век н. э.) подтверждает, что зажигательные стёкла были известны в античности, а именно в римский период . В работах Плиния содержится также самая ранняя из известных ссылок на использование : он упоминает, что Нерон, как говорят, смотрел гладиаторские игры, используя изумруд (предположительно , чтобы исправить близорукость , хотя отсылка не точна) . И Плиний, и Сенека Младший (3 г. до н. э. — 65 г. н. э.) описали увеличивающий эффект стеклянного шара, наполненного водой.

Птолемей (II век) написал книгу по , которая, однако, сохранилась только в латинском переводе с неполного и очень плохого арабского перевода. Однако книга была принята средневековыми учёными в исламском мире и прокомментирована (X век), чей вклад, в свою очередь, был улучшен Альхазеном ( , XI век). Арабский перевод Оптики Птолемея стал доступен в латинском переводе в XII веке ( Евгений Палермский , 1154 г.). Между XI и XIII веками были изобретены « ». Это были примитивные плоско-выпуклые линзы, изначально сделанные путем разрезания стеклянной сферы пополам. Средневековые (XI или XII век) из горного хрусталя могли быть предназначены для использования в качестве зажигательных стёкол, однако возможно, что их изготовили для каких -то иных целей .

Очки были изобретены как усовершенствование «камней для чтения» периода Высокого Средневековья в Северной Италии во второй половине XIII века . Это стало началом развития оптической индустрии шлифовки и полировки линз для очков — сначала в Венеции и Флоренции в конце XIII века , а затем в центрах производства очков в Нидерландах и Германии . Создатели очков сделали улучшенные типы линз для коррекции зрения, основанные больше на эмпирических знаниях, полученных при наблюдении за эффектами линз (вероятно, без знания элементарной оптической теории того времени) . Практические разработки и эксперименты с линзами привели к изобретению составного оптического микроскопа около 1595 года и телескопа-рефрактора в 1608 году — и тот и другой появились в центрах изготовления очков в Нидерландах .

С изобретением телескопа в XVII веке и микроскопа в начале XVIII было проведено множество экспериментов с формами линз в стремлении исправить наблюдаемые в последних хроматические ошибки. Оптики пытались конструировать линзы различной формы кривизны, ошибочно полагая, что ошибки возникли из-за дефектов сферической формы их поверхностей . Оптическая теория преломления и эксперименты показали, что ни один одноэлементный объектив не может сфокусировать все цвета. Это привело к изобретению составной ахроматической линзы в Англии в 1733 году, изобретение также было заявлено англичанином Джоном Доллондом в патенте 1758 года.

Характеристики простых линз

В зависимости от форм различают собирающие (положительные) и рассеивающие (отрицательные) линзы. К группе собирающих линз обычно относят линзы, у которых середина толще их краёв, а к группе рассеивающих — линзы, края которых толще середины. Следует отметить, что это верно только если показатель преломления у материала линзы больше, чем у окружающей среды. Если показатель преломления линзы меньше, ситуация будет обратной. Например пузырёк воздуха в воде — двояковыпуклая рассеивающая линза.

Линзы характеризуются, как правило, своей оптической силой (измеряется в диоптриях ), и фокусным расстоянием .

Для построения оптических приборов с исправленной оптической аберрацией (прежде всего — хроматической, обусловленной дисперсией света , — ахроматы и) важны и иные свойства линз и их материалов, например, показатель преломления , , показатель поглощения и показатель рассеяния материала в выбранном оптическом диапазоне.

Иногда линзы/линзовые оптические системы (рефракторы) специально рассчитываются на использование в средах с относительно высоким показателем преломления (см. ,).

Выпукло-вогнутая линза называется мениском и может быть собирательной (утолщается к середине), рассеивающей (утолщается к краям) или телескопической (фокусное расстояние равно бесконечности). Так, например линзы очков для близоруких — как правило, отрицательные мениски.

Вопреки распространённому заблуждению, оптическая сила мениска с одинаковыми радиусами не равна нулю, а положительна, и зависит от показателя преломления стекла и от толщины линзы. Мениск, центры кривизны поверхностей которого находятся в одной точке называется концентрической линзой (оптическая сила всегда отрицательна).

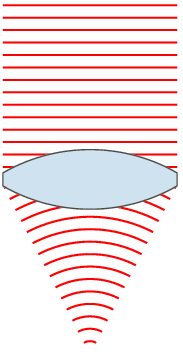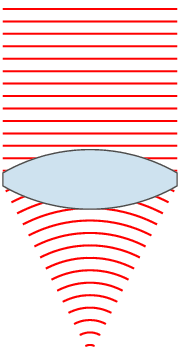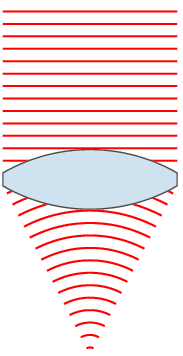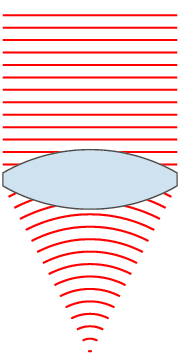
Отличительным свойством собирательной линзы является способность собирать падающие на её поверхность лучи в одной точке, расположенной по другую сторону линзы.

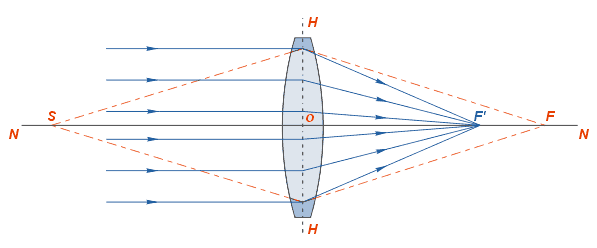
Если на некотором расстоянии перед собирательной линзой поместить светящуюся точку S, то луч света, направленный по оси, пройдёт через линзу не преломившись , а лучи, проходящие не через центр, будут преломляться в сторону оптической оси и пересекутся на ней в некоторой точке F, которая и будет изображением точки S. Эта точка носит название сопряжённого фокуса , или просто фокуса .

Если на линзу будет падать свет от очень удалённого источника, лучи которого можно представить идущими параллельным пучком, то на выходе из неё лучи преломляются под бо́льшим углом, и точка F переместится на оптической оси ближе к линзе. При данных условиях точка пересечения лучей, вышедших из линзы, называется фокусом F’, а расстояние от центра линзы до фокуса — фокусным расстоянием .

Лучи, падающие на рассеивающую линзу, на выходе из неё будут преломляться в сторону краёв линзы, то есть рассеиваться. Если эти лучи продолжить в обратном направлении так, как показано на рисунке пунктирной линией, то они сойдутся в одной точке F, которая и будет фокусом этой линзы. Этот фокус будет мнимым.

Сказанное о фокусе на оптической оси в равной степени относится и к тем случаям, когда изображение точки находится на наклонной линии, проходящей через центр линзы под углом к оптической оси. Плоскость, перпендикулярная оптической оси, расположенная в фокусе линзы, называется фокальной плоскостью .

Собирающие линзы могут быть направлены к предмету любой стороной, вследствие чего лучи при прохождении через линзу могут собираться как с одной, так и с другой её стороны. Таким образом, линза имеет два фокуса — передний и задний . Расположены они на оптической оси по обе стороны линзы на фокусном расстоянии от главных точек линзы.

Часто в технике применяется понятие увеличение линзы ( лупы ) и обозначается как 2×, 3× и т. д. В данном случае увеличение определяется по формуле ${\displaystyle \Gamma _{d}={{F+d} \over {F}}={{d} \over {F}}+1}$ (при рассматривании вплотную к линзе). Где ${\displaystyle F}$ — фокусное расстояние, ${\displaystyle d}$ — расстояние наилучшего зрения (для взрослого человека средних лет около 25 см) . Для линзы с фокусным расстоянием 25 см, увеличение составляет 2×. Для линзы с фокусным расстоянием 10 см, увеличение составляет 3,5×.

Ход лучей в тонкой линзе

Линза, для которой толщина принята равной нулю, в оптике называется «тонкой». Для такой линзы показывают не две главных плоскости , а одну, в которой как бы сливаются вместе передняя и задняя.

Рассмотрим построение хода луча произвольного направления в тонкой собирающей линзе. Для этого воспользуемся двумя свойствами тонкой линзы:

• луч, прошедший через оптический центр линзы, не меняет своего направления;
• параллельные лучи, проходящие через линзу, сходятся в фокальной плоскости.

Рассмотрим луч SA произвольного направления, падающий на линзу в точке A. Построим линию его распространения после преломления в линзе. Для этого построим луч OB, параллельный SA и проходящий через оптический центр O линзы. По первому свойству линзы луч OB не изменит своего направления и пересечёт фокальную плоскость в точке B. По второму свойству линзы параллельный ему луч SA после преломления должен пересечь фокальную плоскость в той же точке. Таким образом, после прохождения через линзу луч SA пойдёт по пути AB.

Аналогичным образом можно построить другие лучи, например луч SPQ.

Обозначим расстояние SO от линзы до источника света через u, расстояние OD от линзы до точки фокусировки лучей через v, фокусное расстояние OF через f. Выведем формулу, связывающую эти величины.

Рассмотрим две пары подобных треугольников: ${\displaystyle \triangle SOA}$ и ${\displaystyle \triangle OFB}$ , ${\displaystyle \triangle DOA}$ и ${\displaystyle \triangle DFB}$ . Запишем пропорции

${\displaystyle {\frac {OA}{u}}={\frac {BF}{f}};\qquad {\frac {OA}{v}}={\frac {BF}{v-f}}.}$

Разделив первую пропорцию на вторую, получим

${\displaystyle {\frac {v}{u}}={\frac {v-f}{f}};\qquad {\frac {v}{u}}={\frac {v}{f}}-1.}$

После деления обеих частей выражения на v и перегруппировки членов, приходим к окончательной формуле

${\displaystyle {\frac {1}{u}}+{\frac {1}{v}}={\frac {1}{f}}}$

где ${\displaystyle f{\frac {}{}}}$ — фокусное расстояние тонкой линзы.

Ход лучей в системе линз

Ход лучей в системе линз строится теми же методами, что и для одиночной линзы.

Рассмотрим систему из двух линз, одна из которых имеет фокусное расстояние OF, а вторая O ₂ F ₂ . Строим путь SAB для первой линзы и продолжаем отрезок AB до вхождения во вторую линзу в точке C.

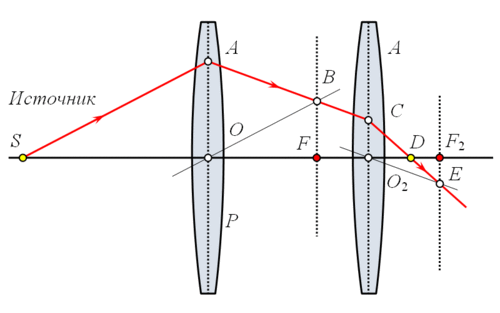
Из точки O ₂ строим луч O ₂ E, параллельный AB. При пересечении с фокальной плоскостью второй линзы этот луч даст точку E. Согласно второму свойству тонкой линзы луч AB после прохождения через вторую линзу пойдёт по пути CE. Пересечение этой линии с оптической осью второй линзы даст точку D, где сфокусируются все лучи, вышедшие из источника S и прошедшие через обе линзы.

Построение изображения тонкой собирающей линзой

При изложении характеристики линз был рассмотрен принцип построения изображения светящейся точки в фокусе линзы. Лучи, падающие на линзу слева, проходят через её задний фокус, а падающие справа — через передний фокус. Следует учесть, что у рассеивающих линз, наоборот, задний фокус расположен спереди линзы, а передний позади.

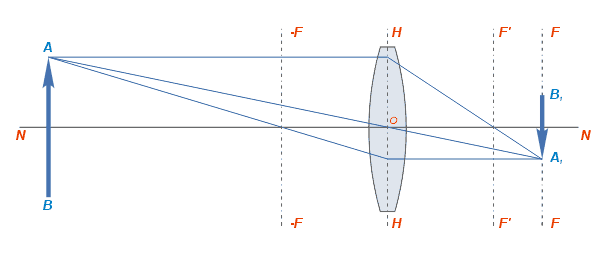
Построение линзой изображения предметов, имеющих определённую форму и размеры, получается следующим образом: допустим, линия AB представляет собой объект, находящийся на некотором расстоянии от линзы, значительно превышающем её фокусное расстояние. От каждой точки предмета через линзу пройдёт бесчисленное количество лучей, из которых, для наглядности, на рисунке схематически изображён ход только трёх лучей.

Три луча, исходящие из точки A, пройдут через линзу и пересекутся в соответствующих точках схода на A ₁ B ₁ , образуя изображение. Полученное изображение является действительным и перевёрнутым .

В данном случае изображение получено в сопряжённом фокусе в некоторой фокальной плоскости FF, несколько удалённой от главной фокальной плоскости F’F’, проходящей параллельно ей через главный фокус.

Далее приведены различные случаи построения изображений предмета, помещённого на различных расстояниях от линзы.

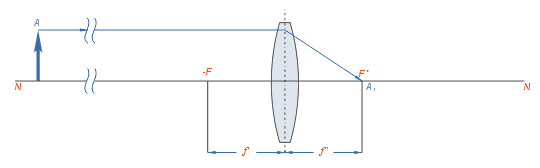
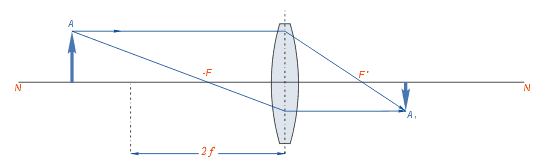
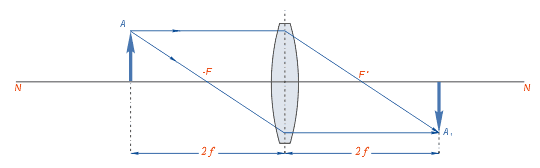
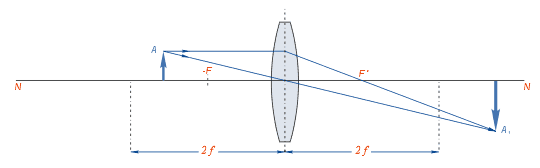
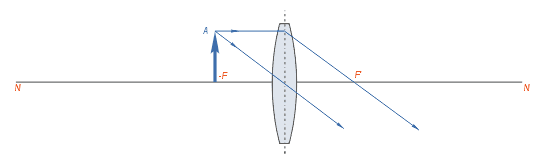
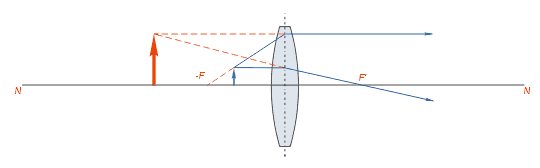
Нетрудно заметить, что при приближении предмета из бесконечности к переднему фокусу линзы изображение удаляется от заднего фокуса и по достижении предметом плоскости переднего фокуса оказывается в бесконечности от него.

Эта закономерность имеет большое значение в практике различных видов фотографических работ, поэтому для определения зависимости между расстоянием от предмета до линзы и от линзы до плоскости изображения необходимо знать основную формулу линзы .

Формула тонкой линзы

Расстояния от точки предмета до центра линзы и от точки изображения до центра линзы называются сопряжёнными фокусными расстояниями .

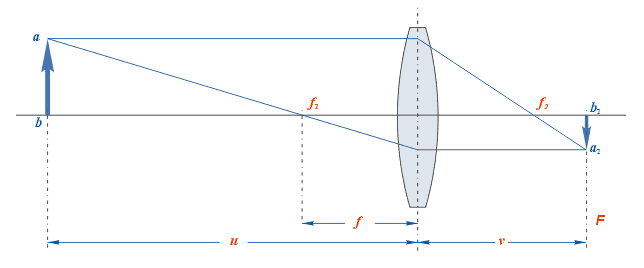
Эти величины находятся в зависимости между собой и определяются формулой, называемой формулой тонкой линзы (впервые полученной Исааком Барроу ):

${\displaystyle {1 \over u}+{1 \over v}={1 \over f}}$

где ${\displaystyle u}$ — расстояние от линзы до предмета; ${\displaystyle v}$ — расстояние от линзы до изображения; ${\displaystyle f}$ — главное фокусное расстояние линзы. В случае толстой линзы формула остаётся без изменения с той лишь разницей, что расстояния отсчитываются не от центра линзы, а от главных плоскостей .

Для нахождения той или иной неизвестной величины при двух известных пользуются следующими уравнениями:

${\displaystyle f={{v\cdot u} \over {v+u}}}$

${\displaystyle u={{f\cdot v} \over {v-f}}}$

${\displaystyle v={{f\cdot u} \over {u-f}}}$

Следует отметить, что знаки величин ${\displaystyle u}$ , ${\displaystyle v}$ , ${\displaystyle f}$ выбираются исходя из следующих соображений — для действительного изображения от действительного предмета в собирающей линзе — все эти величины положительны. Если изображение мнимое — расстояние до него принимается отрицательным, если предмет — расстояние до него отрицательно, если линза рассеивающая — фокусное расстояние отрицательно.

Линейное увеличение

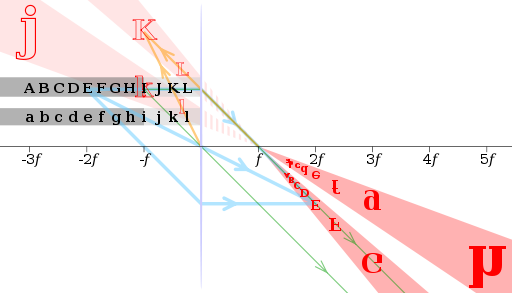
Линейным увеличением ${\displaystyle m={{a_{2}b_{2}} \over {ab}}}$ (для рисунка из предыдущего раздела) называется отношение размеров изображения к соответствующим размерам предмета. Это отношение может быть также выражено дробью ${\displaystyle m={{a_{2}b_{2}} \over {ab}}={v \over u}}$ , где ${\displaystyle v}$ — расстояние от линзы до изображения; ${\displaystyle u}$ — расстояние от линзы до предмета.

Здесь ${\displaystyle m}$ есть коэффициент линейного увеличения, то есть число, показывающее во сколько раз линейные размеры изображения меньше (больше) действительных линейных размеров предмета.

В практике вычислений гораздо удобнее это соотношение выражать в значениях ${\displaystyle u}$ или ${\displaystyle f}$ , где ${\displaystyle f}$ — фокусное расстояние линзы.

${\displaystyle m={f \over {u-f}};\ m={{v-f} \over f}}$ .

Расчёт фокусного расстояния и оптической силы линзы

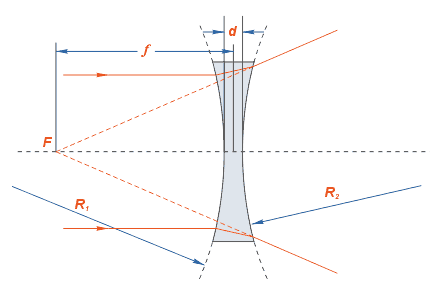
Значение фокусного расстояния для линзы может быть рассчитано по следующей формуле:

${\displaystyle {\frac {n_{0}}{f}}=(n-n_{0})\left\{{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-n_{0})d}{nR_{1}R_{2}}}\right\}}$ , где

${\displaystyle n}$ — показатель преломления материала линзы, ${\displaystyle n_{0}}$ — показатель преломления среды, окружающей линзу,

${\displaystyle d}$ — расстояние между сферическими поверхностями линзы вдоль оптической оси , также известное как толщина линзы ,

${\displaystyle R_{1}}$ — радиус кривизны поверхности, которая ближе к источнику света (дальше от фокальной плоскости),

${\displaystyle R_{2}}$ — радиус кривизны поверхности, которая дальше от источника света (ближе к фокальной плоскости),

Для ${\displaystyle R_{1}}$ в этой формуле, знак радиуса положителен, если поверхность выпуклая, и отрицателен, если вогнутая. Для ${\displaystyle R_{2}}$ наоборот — положителен, если линза вогнутая, и отрицателен, если выпуклая. Если ${\displaystyle d}$ пренебрежительно мало, относительно её фокусного расстояния, то такая линза называется тонкой , и её фокусное расстояние можно найти как:

${\displaystyle {\frac {n_{0}}{f}}=(n-n_{0})\left\{{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right\}.}$

Эту формулу также называют формулой шлифовщика линз . Величина фокусного расстояния положительна для собирающих линз, и отрицательна для рассеивающих. Величина ${\displaystyle {\frac {n_{0}}{f}}}$ называется оптической силой линзы. Оптическая сила линзы измеряется в диоптриях, единицами измерения которых являются м ⁻¹ . Оптическая сила также зависит от показателя преломления окружающей среды ${\displaystyle n_{0}}$ .

Указанные формулы могут быть получены аккуратным рассмотрением процесса построения изображения в линзе с использованием закона Снелла , если перейти от общих тригонометрических формул к параксиальному приближению . Кроме того, для вывода формулы тонкой линзы удобно заменить её треугольной призмой и затем использовать формулу угла отклонения этой призмы .

Линзы симметричны, то есть они имеют одинаковое фокусное расстояние независимо от направления света — слева или справа, что, однако, не относится к другим характеристикам, например, аберрациям , величина которых зависит от того, какой стороной линза повёрнута к свету.

Комбинация нескольких линз (центрированная система)

Линзы могут комбинироваться друг с другом для построения сложных оптических систем. Оптическая сила системы из двух линз может быть найдена как простая сумма оптических сил каждой линзы (при условии, что обе линзы можно считать тонкими и они расположены вплотную друг к другу на одной оси):

${\displaystyle {\frac {1}{F}}={\frac {1}{f_{1}}}+{\frac {1}{f_{2}}}}$ .

Если линзы расположены на некотором расстоянии друг от друга и их оси совпадают (система из произвольного числа линз, обладающих таким свойством, называется центрированной системой), то их общую оптическую силу с достаточной степенью точности можно найти из следующего выражения:

${\displaystyle {\frac {1}{F}}={\frac {1}{f_{1}}}+{\frac {1}{f_{2}}}-{\frac {L}{f_{1}f_{2}}}}$ ,

где ${\displaystyle L}$ — расстояние между главными плоскостями линз.

Недостатки простой линзы

В современных оптических приборах к качеству изображения предъявляются высокие требования.

Изображение, даваемое простой линзой, в силу целого ряда недостатков не удовлетворяет этим требованиям. Устранение большинства недостатков достигается соответствующим подбором ряда линз в центрированную оптическую систему — объектив . Недостатки оптических систем называются аберрациями , которые делятся на следующие виды:

• геометрические аберрации:
  • сферическая аберрация ;
  • кома ;
  • астигматизм ;
  • дисторсия ;
  • кривизна поля изображения ;
• хроматическая аберрация ;
• дифракционная аберрация (эта аберрация вызывается другими элементами оптической системы, и к самой линзе отношения не имеет).

Линзы со специальными свойствами

Линзы из органических полимеров

Полимеры дают возможность создавать недорогие асферические линзы с помощью литья .

В области офтальмологии созданы мягкие контактные линзы . Первыми производителями линз такого вида стала компания Bausch+Lomb . Производство мягких линз основано на применении материалов, имеющих бифазную природу, сочетающих фрагменты кремний-органического или кремний-фторорганического полимера силикона и гидрофильного полимера гидрогеля . Работа в течение более 20 лет привела к созданию в конце 1990-х годов , которые благодаря сочетанию гидрофильных свойств и высокой кислородопроницаемости могут непрерывно использоваться в течение 30 дней круглосуточно.

Линзы из кварцевого стекла

Кварцевое стекло — однокомпонентное стекло , состоящее из диоксида кремния , с незначительным (около 0,01 % и меньше) содержанием примесей Al ₂ О ₃ , СаО и MgO. Оно отличается высокой термостойкостью и инертностью ко многим химическим реактивам за исключением плавиковой кислоты .

Прозрачное кварцевое стекло хорошо пропускает ультрафиолетовые и видимые лучи света .

Линзы из кремния

Кремний хорошо пропускает инфракрасное излучение с длинами волн от 1 до 9 мкм, имеет большой показатель преломления (n = 3,42 при ${\displaystyle \lambda }$ = 6 мкм), и в то же время полностью непрозрачен в видимом диапазоне . Поэтому его применяют при изготовлении линз для ИК-диапазона.

Кроме того, свойства кремния и современные технологии его обработки позволяют создать линзы для рентгеновского диапазона электромагнитных волн .

Просветлённые линзы

Путём нанесения на поверхность линзы многослойных диэлектрических покрытий можно добиться значительного уменьшения отражения света и, вследствие этого, увеличения коэффициента пропускания .Такие линзы легко узнать по фиолетовым бликам: они не отражают зелёный цвет, отражая красный и синий, что в сумме даёт фиолетовый. Подавляющее большинство линз для фототехники производства СССР, в том числе для бытовых объективов, изготавливалось просветлёнными.

Применение линз

Линзы являются широко распространённым оптическим элементом большинства оптических систем .

Традиционное применение линз — бинокли , телескопы , оптические прицелы , теодолиты , микроскопы , фото- и видеотехника . Одиночные собирающие линзы используются как увеличительные стёкла .

Другая важная сфера применения линз — офтальмология , где без них невозможно исправление недостатков зрения — близорукости , дальнозоркости , неправильной аккомодации , астигматизма и других заболеваний. Линзы используют в таких приспособлениях, как очки и контактные линзы . Также существует подвид линз, ночные линзы . Они имеют более жесткую основу и используются исключительно во время сна, для временной коррекции зрения в дневное время.

В радиоастрономии и радарах часто используются диэлектрические линзы, собирающие поток радиоволн в приёмную антенну , либо фокусирующие их на цели.

В конструкции плутониевых ядерных бомб для преобразования сферической расходящейся ударной волны от точечного источника ( детонатора ) в сферическую сходящуюся, применялись линзовые системы, изготовленные из взрывчатки с разной скоростью детонации (то есть с разным показателем преломления).

См. также

• Лентикулярный растр
• Линза Френеля
• Линза Люнеберга
• Билинза Бийе
• Цейс, Карл
• Контактные линзы
• Лупа
• Магнитная линза
• Фокус (физика)
• Оптические системы
• Оптические приборы
• Оптические материалы
• Аберрации оптических систем

Примечания

Литература

• Краткий фотографический справочник / Под общей редакцией д.т.н. В. В. Пуськова. — 2-е изд. — М. : Искусство, 1953.
• Ландсберг Г. С. Оптика. — 5-ое изд. — М. : Наука, 1976.
• Политехнический словарь / глав. ред. А. Ю. Ишлинский . — 3-е изд. — М. : Советская Энциклопедия, 1989.
• Линза // Фотокинотехника: Энциклопедия / Гл. ред. Е. А. Иофис . — М. : Советская энциклопедия , 1981. — 447 с.

Ссылки