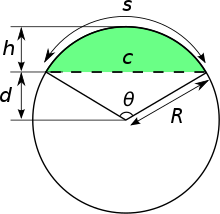
Сегме́нт кру́га , кругово́й сегмент — часть круга , ограниченная дугой окружности и её хордой или секущей .

Соотношения

Пусть ${\displaystyle R}$ — радиус круга, ${\displaystyle c}$ — длина хорды сегмента, ${\displaystyle s}$ — длина дуги сегмента, ${\displaystyle h}$ — высота сегмента, также называемая стрелкой сегмента, ${\displaystyle \theta }$ — угол дуги сегмента выраженный в радианах . Размер сегмента круга однозначно задаётся любой парой этих величин и любая величина выражается через любую другую пару. Тогда:

${\displaystyle R={\frac {s}{\theta }}={\frac {h}{1-\cos {\frac {\theta }{2}}}}={\frac {d}{\cos {\tfrac {\theta }{2}}}}={\frac {c}{2\sin {\tfrac {\theta }{2}}}}=h+d={\frac {c^{2}+4h^{2}}{8h}}={\frac {1}{2}}{\sqrt {4d^{2}+c^{2}}};}$

${\displaystyle s=\theta \cdot R=2R\arccos \left(1-{\tfrac {h}{R}}\right)=2R\arccos {\tfrac {d}{R}}=2R\arcsin {\frac {c}{2R}}=}$

${\displaystyle ={\frac {\theta }{h}}}{1-\cos {\frac {\theta }{2}}={\frac {\theta d}{\cos {\tfrac {\theta }{2}}}}={\frac {\theta c}{2\sin {\tfrac {\theta }{2}}}}=}$

${\displaystyle =2(h+d)\arccos {\tfrac {d}{h+d}}={\frac {c^{2}+4h^{2}}{4h}}}\arcsin {{\tfrac {4hc}{c^{2}+4h^{2}}}=}$

${\displaystyle ={\sqrt {4d^{2}+c^{2}}}}\arcsin {{\frac {c}{\sqrt {4d^{2}+c^{2}}}};}$

${\displaystyle c=2R\sin {\tfrac {\theta }{2}}=R{\sqrt {2-2\cos \theta }}=2{\sqrt {h(2R-h)}};}$

${\displaystyle h=R(1-\cos {\tfrac {\theta }{2}})=R-{\sqrt {R^{2}-{\tfrac {c^{2}}{4}}}};}$

${\displaystyle \theta =2\arccos {\frac {d}{R}}={\frac {s}{R}}=2\arccos {\frac {R-h}{R}}=2\arcsin {\frac {c}{2R}}.}$

Площадь кругового сегмента вычисляется по формуле:

${\displaystyle S={\frac {1}{2}}R^{2}(\theta -\sin \theta)={\frac {1}{2}}R^{2}\left({\frac {s}{R}}-\sin {\tfrac {s}{R}}\right).}$

См. также

• Сектор круга
• Шаровой сегмент
• Шаровой слой
• Коническое сечение
• Дуга окружности
• Разрез