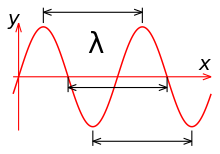
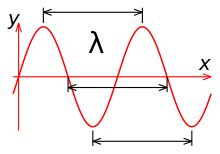
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе .

Длину волны можно также определить:

• как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на ${\displaystyle 2\pi }$ , — данное определение наиболее уместно применительно к линиям передачи ;
• как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
• как пространственный период волнового процесса.

Например, для волны, возникающей в воде от равномерно колеблющегося поплавка, длина волны — это расстояние между двумя соседними гребнями волны, измеренное в какой-то момент времени в радиальном направлении.

Длина волны является одной из основных характеристик волны наряду с частотой , амплитудой , начальной фазой, направлением распространения и поляризацией . Для обозначения длины волны принято использовать греческую букву ${\displaystyle \lambda }$ , размерность длины волны — метр ([м]).

Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному ) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (самой низкочастотной, фундаментальной) гармоники спектра.

Длина волны — пространственный период волнового процесса

Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим ). По аналогии с периодом колебаний ${\displaystyle T}$ [с] (интервалом времени, за который периодический колебательный процесс повторяется и размерность которого — секунда), длину волны ${\displaystyle \lambda }$ [м] можно рассматривать как пространственный период волнового процесса . Следует заметить, что круговой частоте колебания ${\displaystyle \omega =2\pi f=2\pi /T}$ [радиан/с], показывающей, на сколько радиан изменится фаза колебания за 1 с в фиксированной точке (в множестве точек если твердое тело), соответствует «пространственная круговая частота» ${\displaystyle k=2\pi /\lambda }$ [радиан/м], называемая волновым числом и показывающая, на сколько радиан отличаются фазы колебательного процесса в двух точках пространства, расположенных вдоль направления распространения волны на расстоянии 1 м друг от друга. При этом очевидно, что фазы колебательного процесса в двух таких точках, расположенных друг от друга на расстоянии в ${\displaystyle \lambda }$ [м], отличаются ровно на ${\displaystyle 2\pi }$ .

Универсальные соотношения между длиной волны и частотой

Получить соотношение, связывающее длину волны с фазовой скоростью ${\displaystyle v}$ и частотой ${\displaystyle f}$ , можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду ${\displaystyle T}$ колебаний, поэтому

${\displaystyle \lambda =vT={\frac {v}{f}}={\frac {2\pi v}{\omega }}.}$

Эти соотношения являются универсальными для волн любой природы, будь то акустические, электромагнитные или другие.

Случай электромагнитной волны

В вакууме

Для электромагнитных волн в вакууме скорость ${\displaystyle v}$ в выписанной выше формуле равна скорости света в вакууме ${\displaystyle c}$ (299 792 458 м/с), и длина волны составляет

${\displaystyle \lambda ={\frac {299\,792\,458~{\text{m/s}}}{f}}}$ .

Если значение ${\displaystyle f}$ подставить в герцах, то ${\displaystyle \lambda }$ будет выражена в метрах .

Приближённо, с погрешностью около 0,07 % рассчитать длину электромагнитной волны в свободном пространстве можно так: 300 000 км/с делим на частоту в килогерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару ${\displaystyle f}$ ↔ ${\displaystyle \lambda }$ , например, частоте 100 МГц соответствует длина волны 3 м; тогда оценив, во сколько раз требуемая частота выше или ниже 100 МГц , можно определить длину волны. Например, 1 МГц ниже 100 МГц в 100 раз, значит 1 МГц ↔ 3 м × 100 = 300 м

Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц ( радиовещательный FM-диапазон ) — 3 м; 900 (1800) МГц ( мобильные телефоны ) — 33,3 (16,7) см; 2,4 ГГц ( Wi-Fi ) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов- истребителей ) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм .

Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн , степень проявления эффекта дифракции , отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия ) превышают рабочую длину волны радиоэлектронного средства . Магнитная антенна средневолнового радиоприёмника имеет габарит на порядки меньше длины волны, и при этом, тем не менее, обладает пространственной селективностью.

В веществе

Длина электромагнитной волны в среде записывается как

${\displaystyle \lambda ={\frac {c}{nf}},}$

где ${\displaystyle n={\sqrt {\varepsilon \mu }}}$ — показатель преломления вещества, ${\displaystyle \varepsilon }$ , ${\displaystyle \mu }$ — относительная диэлектрическая и магнитная проницаемость, соответственно. Величины ${\displaystyle \varepsilon }$ и ${\displaystyle \mu }$ могут существенно зависеть от частоты ${\displaystyle f}$ (явление дисперсии ), поэтому в формулу должны подставляться ${\displaystyle \varepsilon }$ , ${\displaystyle \mu }$ именно для рассматриваемой частоты, а не, скажем, для статического поля.

Как правило, ${\displaystyle \varepsilon >1}$ (исключения имеют место на предельно высоких — рентгеновских — частотах), а значит, ${\displaystyle n>1}$ и длина волны в среде меньше, чем для той же частоты в вакууме.

Поскольку для большинства сред в радиочастотном диапазоне ${\displaystyle \mu \approx 1}$ (для диэлектриков ${\displaystyle \mu =1}$ , для ферромагнетиков с ростом частоты ${\displaystyle \mu \rightarrow 1}$ ), то в инженерной практике используют величину ${\displaystyle 1/{\sqrt {\varepsilon }}<1}$ , которую называют коэффициентом укорочения . Она равна отношению длины волны в среде к длине волны в вакууме. Например, для полиэтилена (используется в радиочастотном диапазоне как изоляционный материал с малыми потерями) ${\displaystyle \varepsilon }$ = 2,56, и коэффициент укорочения ${\displaystyle 1/{\sqrt {\varepsilon }}}$ = 1/1,6 = 0,625.

Специфический случай представляют волноводы . В них длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) может быть не только больше, чем в среде с тем же значением ${\displaystyle \varepsilon }$ , но и больше, чем вакууме, так как фазовая скорость электромагнитной волны в волноводе превышает скорость электромагнитной волны в среде с тем же ${\displaystyle \varepsilon }$ .

Случай акустической (упругой) волны

Универсальное соотношение «длина волны — частота» полностью сохраняет актуальность в акустике, с тем уточнением, что под ${\displaystyle v}$ понимается скорость звука в той конкретной среде (воздух, твёрдое тело), в которой рассматривается распространение упругой волны. Например, длина звуковой волны в воздухе связана с частотой как

${\displaystyle \lambda ={\frac {332+0.6\Theta }{f}}}$ ,

где ${\displaystyle \Theta }$ — температура в градусах Цельсия, ${\displaystyle f}$ — частота в Гц, а длина волны ${\displaystyle \lambda }$ получается в метрах . В вакууме, естественно, никаких звуковых волн (в отличие от электромагнитных) быть не может.

Случай квантовомеханической волны де Бройля

Волнам де Бройля в квантовой механике также соответствует определённая длина волны. Частице с энергией ${\displaystyle E}$ и импульсом ${\displaystyle p}$ , соответствуют:

• частота: ${\displaystyle f={\frac {E}{h}},}$
• длина волны: ${\displaystyle \lambda ={\frac {h}{p}},}$

где ${\displaystyle h}$ — постоянная Планка .

Примечания

Литература

• Волны де Бройля / В. И. Григорьев // Вешин — Газли. — М. : Советская энциклопедия, 1971. — ( Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
• Длина волны // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — ( Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).

Для улучшения этой статьи желательно : Найти и оформить в виде сносок ссылки на независимые авторитетные источники , подтверждающие написанное . Оформить статью по правилам . После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки.