Interested Article - Евдокс Книдский

- 2021-04-25
- 1
Евдо́кс Кни́дский (в части источников: Эвдокс , др.-греч. Εὔδοξος , лат. Eudoxus ; ок. 408 год до н. э. — ок. 355 год до н. э. ) — древнегреческий математик , механик и астроном . Занимался также врачеванием, философией и музыкой ; был известен как оратор и законовед.
Неоднократно упоминается у античных авторов. Сочинения самого Евдокса до нас не дошли, но его математические открытия изложены в « Началах Евклида ». Среди его учеников были Каллипп , Менехм и Динострат .
Научная школа Евдокса сыграла большую роль в развитии античной астрономии и математики . Историки науки относят Евдокса к числу основоположников интегрального исчисления и теоретической астрономии . В частности, Евдокс создал теорию геометрических величин (античный аналог вещественных чисел ), метод исчерпывания (прообраз анализа криволинейных фигур) и первую теоретическую модель движения небесных тел , переработанный вариант которой был позднее изложен в « Альмагесте » Птолемея .
В честь Евдокса названы:
- кривая Евдокса ;
- кратер на Луне ;
- .
Биография
О жизни Евдокса известно немного. Родился в Книде , на юго-западе Малой Азии . Учился медицине у Филистиона в Сицилии , потом математике (у пифагорейца Архита в Италии ), далее присоединился к школе Платона в Афинах . Около года провёл в Египте , изучал астрономию в Гелиополе . Позднее Евдокс переселился в город Кизик на Мраморном море , основал там собственную математико-астрономическую школу, читал лекции по философии, астрономии и метеорологии .
Около 368 года до н. э. Евдокс вместе с частью учеников вернулся в Афины. Умер в родном Книде, окружённый славой и почётом. Диоген Лаэртский сообщает некоторые подробности: скончался Евдокс на 53-м году жизни, были у него три дочери и сын по имени Аристагор .
Астрономия
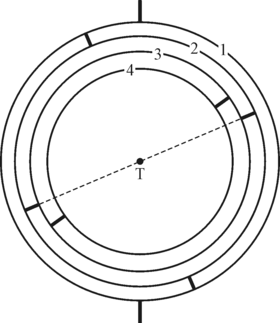
Евдокса можно считать создателем античной теоретической астрономии как самостоятельной науки. В Кизике им была построена обсерватория , в которой впервые в Элладе велись систематические наблюдения за небом. Школа Евдокса выпустила первый в Греции звёздный каталог . Гиппарх упоминал названия двух астрономических трудов Евдокса: «Явления» и «Зеркало» .
Евдокс первым решил задачу Платона , предложившего астрономам построить кинематическую модель , в которой видимые движения Солнца, Луны и планет получались бы как результат комбинации равномерных круговых движений. Модель Евдокса состояла из 27 взаимосвязанных сфер, вращающихся вокруг Земли ( теория гомоцентрических сфер ). Согласие этой модели с наблюдениями было для того времени неплохим; исключением было движение Марса, который неравномерно движется по орбите, далёкой от круговой, и её крайне трудно приблизить равномерным вращением сфер.
Теорию Евдокса с математической точки зрения усовершенствовал Каллипп , у которого число сфер возросло до 34. Дальнейшее усовершенствование теории было связано с Аристотелем , который разработал механизм передачи вращения от наружных сфер к внутренним; при этом число сфер возросло до 56. В дальнейшем Гиппарх и Клавдий Птолемей отказались от теории гомоцентрических сфер в пользу теории эпициклов , которая позволяет более точно смоделировать неравномерность видимого движения небесных тел.
Евдокс считал Землю шарообразным телом, ему приписывается одна из первых оценок длины земного меридиана в 400 000 стадиев , или примерно 70 000 км. Евдокс пытался определить сравнительную величину небесных тел. Он знал, что Солнце больше Луны, но ошибочно полагал, что отношение их диаметров равно 9:1 . Ему же приписывают определение угла между эклиптикой и небесным экватором , то есть, с современной точки зрения, наклона земной оси к плоскости земной орбиты, равного 24° . Евдоксу приписывают также изобретение горизонтальных солнечных часов .
Евдокс был знаком с вавилонской астрологией , относился к ней презрительно и чётко отделял от астрономии: « не следует доверять ни в малейшей степени халдеям и их предсказаниям и утверждениям о жизни человека, основанным на дне его рождения » .
Математика
Евдокс получил фундаментальные результаты в различных областях математики. Например, при разработке своей астрономической модели он существенно продвинул сферическую геометрию . Однако особенно большое значение имели созданные им две классические теории.
Общая теория отношений
Числовые системы древних греков ограничивались натуральными числами и их отношениями (дробями, рациональными числами ). Однако ещё пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, то есть отношение их длин не может быть представлено рациональным числом. Стало понятно, что пифагорейская арифметика должна быть каким-то образом расширена с тем, чтобы включать все результаты измерений. Это и сделал Евдокс. Его теория дошла до нас в изложении Евклида ( Начала , книга V) .
В дополнение к числам Евдокс ввёл более широкое понятие геометрической величины , то есть длины отрезка, площади или объёма. С современной точки зрения, число при таком подходе есть отношение двух однородных величин — например, исследуемой и единичного эталона . Этот подход снимает проблему несоизмеримости. По существу, теория отношений Евдокса — это геометрическая модель вещественных чисел . Следует, однако, подчеркнуть, что Евдокс остался верен прежней традиции — он не рассматривал такое отношение как число; из-за этого в «Началах» многие теоремы о свойствах чисел затем заново доказываются для величин . Признание иррациональностей как особого вида чисел произошло много позднее, под влиянием индийских и исламских математических школ .
В начале своего построения Евдокс дал аксиоматику для сравнения величин. Все однородные величины сравнимы между собой, и для них определены две операции: отделение части и соединение (взятие кратного). Однородность величин сформулирована в виде аксиомы, известной также как аксиома Архимеда : «Говорят, что величины имеют отношение между собой, если они, взятые кратно, могут превзойти друг друга» . Сам Архимед при изложении этой аксиомы сослался на Евдокса .
Далее Евдокс рассматривает отношения между величинами и определяет для них равенство :
Говорят, что величины находятся в том же отношении: первая ко второй и третья к четвёртой, если равнократные первой и третьей одновременно больше, или одновременно равны, или одновременно меньше равнократных второй и четвёртой, каждая каждой при какой бы то ни было кратности, если взять их в соответственном порядке.
В переводе на современный математический язык это означает, что отношения и равны, если для любых натуральных выполняется одно из трёх соотношений:
- либо и ;
- либо и ;
- либо и .
Фактически описанное свойство означает, что между и нельзя вставить рациональное число . До Евдокса использовалось другое определение, через равенство последовательных вычитаний ; это определение эквивалентно определению Евдокса, но сложнее в использовании. Современным языком это можно выразить как равенство цепных дробей для отношений и .
Далее Евдокс аккуратно выводит свойства отношений: транзитивность , упорядоченность и т. д.
Классическая теория Дедекинда для построения вещественных чисел поразительно похожа на изложение Евдокса. Соответствие между ними устанавливается так: пусть заданы две величины Евдокса ; дробь отнесём к классу , если , иначе — к классу . Тогда классы и определяют дедекиндово сечение поля рациональных чисел . Осталось отождествить отношение по Евдоксу с этим дедекиндовым числом .
Отметим, однако, что у Евдокса отсутствует аналог аксиомы непрерывности , и ниоткуда не следует, что всякое сечение определяет вещественное число .
Метод исчерпывания
Это своего рода античный анализ криволинейных фигур. Обоснование этого метода не опирается на актуальные бесконечно малые , но неявно включает понятие предела . Название «метод исчерпывания» предложил в 1647 году Грегуар де Сен-Венсан , в античные времена у метода не было специального названия. Евклид изложил теорию метода исчерпывания в X книге « Начал », а в XII книге применил для доказательства нескольких теорем.

Метод заключался в следующем: для нахождения площади (или объёма) некоторой фигуры в эту фигуру вписывалась монотонная последовательность других фигур и доказывалось, что их площади (объёмы) неограниченно приближаются к площади (объёму) искомой фигуры. Затем вычислялся предел последовательности площадей (объёмов), для чего выдвигалась гипотеза, что он равен некоторому A и доказывалось, что обратное приводит к противоречию. Поскольку общей теории пределов не было (греки избегали понятия бесконечности), все эти шаги, включая обоснование единственности предела, повторялись для каждой задачи .
В такой форме метод исчерпывания хорошо вписывался в строго дедуктивное построение античной математики, однако имел несколько существенных недостатков. Во-первых, он был исключительно громоздким. Во-вторых, не было никакого общего метода для вычисления предельного значения A; Архимед , например, нередко выводил его из механических соображений или просто интуитивно угадывал. Наконец, этот метод не пригоден для нахождения площадей бесконечных фигур .
С помощью метода исчерпывания Евдокс строго доказал ряд уже известных в те годы открытий (площадь круга , объём пирамиды и конуса ) .
Наиболее плодотворным этот метод стал в руках выдающегося последователя Евдокса, Архимеда , который смог его значительно усовершенствовать и виртуозно применял для многих новых открытий . В средние века европейские математики также применяли метод исчерпывания, пока он не был вытеснен сначала более мощным и технологичным методом неделимых , а затем — математическим анализом .
См. также
Примечания
- Boyer Carl B. A History of Mathematics. — 2nd edition. — John Wiley & Sons< Inc., 1991. — P. 92. — 736 p. — ISBN 978-0471543978 .
- Рожанский И. Д. Античная наука. — М. : Наука, 1980. — С. 97. — 198 с. — (История науки и техники).
- , с. 95—96.
- .
- ↑ , с. 306—308.
- Рожанский И. Д. Античная наука. — М. : Наука, 1980. — С. 104. — 198 с. — (История науки и техники).
- James Oliver Thomson. History of ancient geography. Biblo & Tannen Publishers, Cambridge: Cambridge University Press, 1948, ISBN 0-8196-0143-8 , p. 116.
- Andrew Gregory. от 30 декабря 2013 на Wayback Machine , p. 23: «We do not know what value for the inclination of the ecliptic was used by Eudoxus and Callippus, though 24°, 1/15 of a circle, is commonly supposed».
- , с. 188.
- ↑ , с. 96—101.
- Именно так определяли общее понятие числа Ньютон и другие математики Нового времени.
- , с. 309—323.
- , с. 148.
- , Том V.
- Топика Аристотеля
- Von Fritz, Kurt. «The discovery of incommensurability by Hippasus of Metapontum.» Annals of mathematics (1945): 242—264.
- ↑ , с. 97—98, 101.
- ↑ , с. 101—105.
- , с. 168—169.
Литература
- Башмакова И. Г. Лекции по истории математики в Древней Греции // Историко-математические исследования . — М. : Физматгиз , 1958. — № 11 . — С. 306—346 .
- Бурбаки Н. Архитектура математики. Очерки по истории математики. — М. : Иностранная литература, 1963.
- Ван дер Варден Б. Л. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М. : ГИФМЛ, 1959.
- Гейберг И. Л. Естествознание и математика в классической древности. — М. — Л. : ОНТИ, 1936.
- Диоген Лаэртский . . — М. : Иностранная литература, 1979.
- Еремеева А. И., Цицин Ф. А. История астрономии. — М. : Изд-во МГУ, 1989. — ISBN 5-211-00347-0 .
- Житомирский С. В. Античная астрономия и орфизм. — М. : Янус-К, 2001. — ISBN 5-8037-0072-X .
- Житомирский С. В. Планетарная гипотеза Евдокса и древняя мифология // Астрономия древних обществ. — М. : Наука, 2002. — С. 311—314. — ISBN 5-02-008768-8 .
- Зайцев А. И. // Некоторые проблемы истории античной науки : Сборник научных трудов / Отв. ред. А. И. Зайцев, Б. И. Козлов . — Л. : Главная астрономическая обсерватория , 1989. — С. 116—120 . 8 июля 2013 года.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича , в трёх томах. — М. : Наука, 1970. — Т. I.
- Колчинский И.Г., Корсунь А.А., Родригес М.Г. Астрономы: Биографический справочник. — 2-е изд., перераб. и доп. — Киев: Наукова думка, 1986. — 512 с.
- Лишевский В. П. Первый астроном // Земля и Вселенная. — 1992. — № 5 . — С. 43—44 .
- . — М. — Л. : ГТТИ, 1948. — Т. V.
- Паннекук А. История астрономии. — М. : Наука, 1966.
- Fowler D. H. Eudoxus: Parapegmata and Proportionality // Ancient and Medieval trends in the exact sciences. — Stanford: CSLI Publications, 2000. — P. 33—48.
- Goldstein B. R., Bowen A. C. A new view of early Greek astronomy // Isis. — 1983. — № 74 (273) . — P. 330—340.
- Knorr W. R. Plato and Eudoxus on the planetary motions // Journal for the History of Astronomy. — 1990. — № 21 . — P. 313—329.
- Mendell H. Reflections on Eudoxus, Callippus and their Curves: Hippopedes and Callippopedes // Centaurus. — 1998. — № 40 . — P. 177—275.
- Riddel R. C. Eudoxan mathematics and the Eudoxan spheres // Archive for History of Exact Sciences . — 1979. — № 20 . — P. 1—19.
- Wright L. The astronomy of Eudoxus: geometry or physics? // Stud. Hist. and Phil. Sci. — 1973. — № 4 . — P. 165—172.
- Yavetz I. On the homocentric spheres of Eudoxus // Archive for History of Exact Sciences . — 1998. — № 52 . — P. 221—278.
- Yavetz I. A new role for the hippopede of Eudoxus // Archive for History of Exact Sciences . — 2001. — № 56 . — P. 69—93.
Ссылки
- Родин А. В. . Дата обращения: 27 июня 2015.
- Джон Дж. О’Коннор и Эдмунд Ф. Робертсон . (англ.) — биография в архиве MacTutor .
- McConnell C. S. (англ.) . Дата обращения: 8 ноября 2014. Архивировано из 19 июля 2011 года.
- Mendell H. (англ.) . Дата обращения: 8 ноября 2014. 16 мая 2011 года.
- Vicentini M. (англ.) (недоступная ссылка — ) . Дата обращения: 8 ноября 2014.
- 2021-04-25
- 1

































