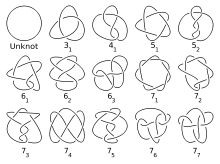
В теории узлов число пересечений узла — это наименьшее число пересечений на любой диаграмме узла. Число пересечений является инвариантом узла .

Примеры

В качестве примера: тривиальный узел имеет нулевое число пересечений, число пересечений трилистника равно трём, а число пересечений восьмёрки равно четырём. Больше нет узлов с числом пересечений четыре и меньше, и есть только два узла с числом пересечений пять, но число узлов с конкретными числами пересечений быстро растёт по мере роста числа пересечений.

Таблицы

Таблицы простых узлов традиционно индексируются числом пересечений с дополнительным описанием, какой именно узел из множества узлов с заданным числом пересечений имеется в виду (это упорядочение не базируется на каких-либо свойствах, за исключением торических узлов , для которых скрученные узлы перечисляются первыми). Список начинается с 3 ₁ (трилистник), 4 ₁ (восьмёрка), 5 ₁ , 5 ₂ , 6 ₁ , и так далее. Этот порядок существенно не изменился со времён Тэта , опубликовавшего таблицу в 1877 году .

Аддитивность

Имеется очень малый прогресс в понимании поведения числа пересечений при элементарных операциях на узлах. Большой открытый вопрос — является ли число пересечений аддитивной по отношению к операции конкатенации . Также ожидается, что сателлитный узел узла K будет иметь большее число пересечений, чем K , но это не доказано.

Аддитивность числа пересечений конкатенации узлов доказана для специальных случаев, например, если исходные узлы являются альтернированными или если исходные узлы являются торическими . Марк Лакенбай дал доказательство, что существует константа N > 1, такая что ${\displaystyle {\frac {1}{N}}(\mathrm {cr} (K_{1})+\mathrm {cr} (K_{2}))\leq \mathrm {cr} (K_{1}+K_{2})}$ , но его метод, использующий , не может улучшить N до 1 .

Приложение в биоинформатике

Имеется странная связь между числом пересечений узла и физическим поведением узлов ДНК . Для простых узлов ДНК число пересечений является хорошим предсказателем относительной скорости узла ДНК электрофореза геля агарозы. В основном, более высокое число пересечений приводит к большей относительной скорости .

Связанные инварианты

Имеются связанные понятия и асимптотического числа пересечений. Оба этих понятия определяют границы стандартного числа пересечений. Есть гипотеза, что асимптотическое число пересечений равно числу пересечений.

Другие числовые инварианты узла включают число мостов , коэффициент зацепления , число отрезков и число распутывания .

Примечания

Литература

• Simon Jonathan. Energy functions for knots: Beginning to predict physical behavior // Mathematical Approaches to Biomolecular Structure and Dynamics / Jill P. Mesirov, Klaus Schulten, De Witt Sumners. — 1996. — Т. 82. — (The IMA Volumes in Mathematics and its Applications). — doi : .
• P. G. Tait. On Knots I, II, III // Scientific papers. — Cambridge University Press, 1898. — Т. 1.
• C. A. Adams. . — American Mathematical Society, 2004. — ISBN 9780821836781 .
• H. Gruber. . — 2003. — arXiv : .
• Yuanan Diao. The additivity of crossing numbers // Journal of Knot Theory and its Ramifications. — 2004. — Т. 13 , вып. 7 . — doi : .
• Marc Lackenby. // Journal of Topology. — 2009. — Т. 2 , вып. 4 . — doi : .