Тессеракт
Тип	Правильный четырёхмерный политоп
Символ Шлефли	{4,3,3}
Ячеек	8
Граней	24
Рёбер	32
Вершин	16
Вершинная фигура	Правильный тетраэдр
Двойственный политоп	16-ячейник

Тессера́кт (от др.-греч. τέσσαρες ἀκτῖνες — «четыре луча») — четырёхмерный гиперкуб , аналог обычного трёхмерного куба в четырёхмерном пространстве . Другие названия: 4-куб , тетраку́б , восьмияче́йник , октахо́р (от др.-греч. οκτώ «восемь» + χώρος «место, пространство»), гиперкуб (если число измерений не оговаривается). Тессеракт — один из шести правильных многоячейников в четырёхмерном пространстве.

Согласно Оксфордскому словарю , слово «тессеракт» было придумано Чарльзом Говардом Хинтоном (1853—1907) и впервые использовано в 1888 году в его книге «Новая эра мысли».

Геометрия

Обычный тессеракт в евклидовом четырёхмерном пространстве определяется как выпуклая оболочка точек (±1, ±1, ±1, ±1). Иначе говоря, он может быть представлен в виде следующего множества:

${\displaystyle [-1,1]^{4}\equiv \{(x_{1},x_{2},x_{3},x_{4})\,:\,-1\leq x_{i}\leq 1\}.}$

Тессеракт ограничен восемью гиперплоскостями ${\displaystyle x_{i}=\pm 1,\;i=1,2,3,4}$ , пересечение которых с самим тессерактом задаёт его трёхмерные грани (являющиеся обычными кубами). Каждая пара непараллельных трёхмерных граней пересекается, образуя двумерные грани (квадраты), и так далее. Окончательно, тессеракт обладает 8 трёхмерными гранями, 24 двумерными, 32 рёбрами и 16 вершинами.

Четырёхмерный гиперобъём тессеракта со стороной длины a рассчитывается по формуле:
${\displaystyle V_{4}=a^{4}}$

Объём же гиперповерхности тессеракта можно найти по формуле:
${\displaystyle V_{3}({\text{hypersurface}})=8a^{3}}$

Радиус описанной гиперсферы:
${\displaystyle R=a}$

Радиус вписанной гиперсферы:
${\displaystyle r={\frac {a}{2}}}$

Популярное описание

Попытаемся представить себе, как будет выглядеть гиперкуб, не выходя из трёхмерного пространства .

В одномерном «пространстве» — на линии — выделим отрезок АВ длиной L. На двумерной плоскости на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат CDBA. Повторив эту операцию с плоскостью, получим трёхмерный куб CDBAEGHF. А сдвинув куб в четвёртом измерении (перпендикулярно первым трём) на расстояние L, мы получим гиперкуб CDBAGHFEKLJIOPNM.

Одномерный отрезок АВ служит стороной двумерного квадрата CDBA, квадрат — стороной куба CDBAEGHF, который, в свою очередь, будет стороной четырёхмерного гиперкуба. Отрезок прямой имеет две граничные точки, квадрат — четыре вершины, куб — восемь. В четырёхмерном гиперкубе, таким образом, окажется 16 вершин: 8 вершин исходного куба и 8 сдвинутого в четвёртом измерении. Он имеет 32 ребра — по 12 дают начальное и конечное положения исходного куба, и ещё 8 рёбер «нарисуют» восемь его вершин, переместившихся в четвёртое измерение. Те же рассуждения можно проделать и для граней гиперкуба. В двумерном пространстве она одна (сам квадрат), у куба их 6 (по две грани от переместившегося квадрата и ещё четыре опишут его стороны). Четырёхмерный гиперкуб имеет 24 квадратные грани — 12 квадратов исходного куба в двух положениях и 12 квадратов от двенадцати его рёбер.

Как сторонами квадрата являются 4 одномерных отрезка, а сторонами (гранями) куба являются 6 двухмерных квадратов, так и для «четырёхмерного куба» (тессеракта) сторонами являются 8 трёхмерных кубов. Пространства противоположных пар кубов тессеракта (то есть трёхмерные пространства, которым эти кубы принадлежат) параллельны. На рисунке это кубы: CDBAEGHF и KLJIMOPN, CDBAKLJI и GHFEOPNM, EFBAMNJI и GHDCOPLK, CKIAGOME и DLJBHPNF.

Аналогичным образом можно продолжить рассуждения для гиперкубов большего числа измерений, но гораздо интереснее посмотреть, как для нас, жителей трёхмерного пространства, будет выглядеть четырёхмерный гиперкуб. Воспользуемся для этого уже знакомым методом аналогий.

Возьмём проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединённые четырьмя линиями — боковыми рёбрами. Аналогичным образом четырёхмерный гиперкуб в пространстве трёх измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединённых восемью рёбрами. При этом сами «ящики» — трёхмерные грани — будут проецироваться на «наше» пространство, а линии, их соединяющие, протянутся в направлении четвёртой оси. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.

Подобно тому, как трёхмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвёртое измерение, сформирует гиперкуб. Его ограничивают восемь кубов, которые в перспективе будут выглядеть как некая довольно сложная фигура. Сам же четырёхмерный гиперкуб состоит из бесконечного количества кубов, подобно тому как трёхмерный куб можно «нарезать» на бесконечное количество плоских квадратов.

Разрезав шесть граней трёхмерного куба, можно разложить его в плоскую фигуру — развёртку . Она будет иметь по квадрату с каждой стороны исходной грани плюс ещё один — грань, ей противоположную. А трёхмерная развёртка четырёхмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс ещё одного — конечной «гиперграни».

Свойства тессеракта представляют собой продолжение свойств геометрических фигур меньшей размерности в четырёхмерное пространство.

Развёртки тессеракта

Аналогично тому, как поверхность куба может быть развёрнута в многоугольник, состоящий из шести квадратов , поверхность тессеракта может быть развёрнута в трёхмерное тело, состоящее из восьми кубов .

Существует 261 развёртка тессеракта . Развёртки гиперкуба могут быть найдены перечислением «сдвоенных деревьев», где «сдвоенное дерево» ( paired tree ) — это дерево с чётным числом вершин, которые разбиты на пары так, что ни одна пара не состоит из двух смежных вершин. Между «сдвоенными деревьями» с 8 вершинами и развёртками тессеракта существует взаимно однозначное соответствие . Всего существует 23 дерева с 8 вершинами, при разбиении вершин которых на пары несмежных вершин получается 261 «сдвоенное дерево» с 8 вершинами .

Крестообразная развёртка тессеракта является элементом картины Сальвадора Дали « Corpus Hypercubus » (1954) .

В рассказе Роберта Хайнлайна « Дом, который построил Тил » калифорнийский архитектор Квинтус Тил строит дом в форме развёртки гиперкуба, который во время землетрясения складывается в тессеракт .

Проекции

На двумерное пространство

Данная структура сложна для воображения, но возможно спроецировать тессеракт в двумерные или трёхмерные пространства . Кроме того, проецирование на плоскость позволяет легко понять расположение вершин гиперкуба. Таким образом, можно получить изображения, которые больше не отражают пространственные отношения в пределах тессеракта, но которые иллюстрируют структуру связи вершин, как в предыдущих примерах:

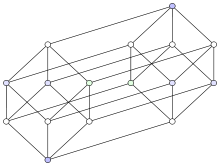
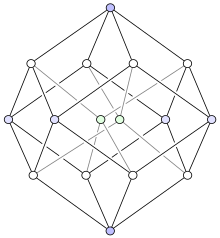
На трёхмерное пространство

Одна из проекций тессеракта на трёхмерное пространство представляет собой два вложенных трёхмерных куба, соответствующие вершины которых соединены между собой отрезками. Внутренний и внешний кубы имеют разные размеры в трёхмерном пространстве, но в четырёхмерном пространстве это равные кубы. Для понимания равности всех кубов тессеракта была создана вращающаяся модель тессеракта.

• Шесть усечённых пирамид по краям тессеракта — это изображения равных шести кубов. Однако эти кубы для тессеракта — как квадраты (грани) для куба. Но на самом деле тессеракт можно разделить на бесконечное количество кубов, как куб — на бесконечное количество квадратов, или квадрат — на бесконечное число отрезков.

Ещё одна интересная проекция тессеракта на трёхмерное пространство представляет собой ромбододекаэдр с проведёнными четырьмя его диагоналями, соединяющими пары противоположных вершин при больших углах ромбов. При этом 14 из 16 вершин тессеракта проецируются в 14 вершин ромбододекаэдра , а проекции 2 оставшихся совпадают в его центре. В такой проекции на трёхмерное пространство сохраняются равенство и параллельность всех одномерных, двухмерных и трёхмерных сторон.

Стереопара

Стереопара тессеракта изображается как две проекции на плоскость одного из вариантов трёхмерного представления тессеракта. Стереопара рассматривается так, чтобы каждый глаз видел только одно из этих изображений, возникает стереоскопический эффект, позволяющий лучше воспринять проекцию тессеракта на трёхмерное пространство.

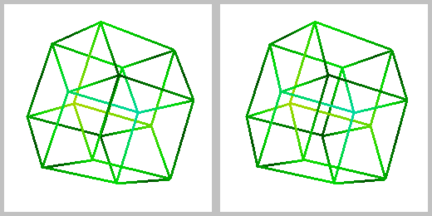
Тессеракт в культуре

• В рассказе « Дом, который построил Тил » ( англ. And He Built a Crooked House ; «И построил он себе скрюченный домишко») Роберта Хайнлайна описан восьмикомнатный дом в форме развёрнутого тессеракта.
• Рассказ Генри Каттнера « Все тенали бороговы » ( англ. Mimsy Were the Borogoves ) описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт.
• В рассказе Роберта Шекли «Мисс Мышка и четвёртое измерение» писатель-эзотерик, знакомец автора, пытается увидеть тессеракт, часами глядя на сконструированный им прибор: шар на ножке с воткнутыми в него стержнями, на которые насажены кубы, обклеенные всеми подряд эзотерическими символами. В рассказе упоминается труд Хинтона.
• В фантастическом рассказе Марка Клифтона «На ленте Мёбиуса» дети-вундеркинды путешествуют через пространство и время, используя модели ленты Мёбиуса , бутылки Клейна и тессеракта.
• В Кинематографической вселенной Marvel Тессеракт является артефактом-носителем одного из шести Камней Бесконечности .
• Сюжет фильма Анджея Секулы « Куб 2: Гиперкуб » разворачивается внутри лабиринта из комнат, помещённого в гиперкуб.
• В научно-фантастическом фильме « Интерстеллар » главный герой Джозеф Купер и робот ТАРС после пересечения горизонта событий Гаргантюа – сверхмассивной чёрной дыры – оказываются внутри массивного тессеракта, построенного людьми будущего.
• Британская прогрессив-рок группа Tesseract , считающаяся одним из пионеров джент -направления в прогрессивном метале, отличается сложными композициями со сменяющимися ритмами.

Примечания

Литература

• Charles H. Hinton. Fourth Dimension, 1904. ISBN 0-405-07953-2
• Gardner M. . — Washington, D.C.: MAA , 1989. — P. 41—54, 272. — ISBN 0-88385-448-1 .
• Ian Stewart, Concepts of Modern Mathematics, 1995. ISBN 0-486-28424-7
• Гальперин Г.А. Многомерный куб. — М. : МЦНМО , 2015. — 80 с. — ISBN 978-5-4439-0296-8 .
• Дужин С., Рубцов В. // Квант . — 1986. — № 6 . — С. 3—7 .

Ссылки

На русском языке

На английском языке

• — программа вывода тессеракта ( Tesseract Trainer , лицензия совместима с GPLv2) и шутер от первого лица в четырёхмерном пространстве ( Adanaxis ; графика, в основном, трёхмерная; есть версия под GPL в репозиториях ОС).

Основные выпуклые правильные и однородные политопы в размерностях 2—10
	A n	B n	I₂(p) / D n	E₆ / / E₈ / F₄ / G₂
Правильный многоугольник	Правильный треугольник	Квадрат	Правильный p-угольник	Правильный шестиугольник	Правильный пятиугольник
Однородный многогранник	Правильный тетраэдр	Правильный октаэдр • Куб	Полукуб		Правильный додекаэдр • Правильный икосаэдр
	Пятиячейник	16-ячейник •	Полутессеракт	24-ячейник	120-ячейник • 600-ячейник
	Правильный 5-симплекс	5-ортоплекс • 5-гиперкуб	5-полугиперкуб
	Правильный 6-симплекс	6-ортоплекс • 6-гиперкуб		•
	Правильный 7-симплекс	• 7-гиперкуб		• •
	Правильный 8-симплекс	• 8-гиперкуб		• •
	Правильный 9-симплекс	• 9-гиперкуб
	Правильный 10-симплекс	• 10-гиперкуб
Однородный n - политоп	Правильный n - симплекс	n - ортоплекс • n - гиперкуб	n - полугиперкуб	• •	n - пятиугольный многогранник
Темы: Семейства политопов • Правильные политопы • Список правильных политопов и их соединений