Пропорционирование ( нем. Proportionierung , от лат. pro-portio — соотношение, соразмерность) — способ гармонизации формы на основе равенства количественных отношений её частей. Пропорциональностью называют равенство (постоянство) отношений двух или более переменных величин . Иную редакцию той же закономерности даёт Большая российская энциклопедия : «Равенство между двумя отношениями четырёх величин» . В математике пропорцией называется такое отношение (зависимость) величин, которое при увеличении или уменьшении одной величины в несколько раз (удвоении, утроении, уменьшении вдвое, …) другая увеличивается или уменьшается во столько же раз. Например, 1 : 2 = 3 : 6. Отношение таких величин называется коэффициентом пропорциональности или константой пропорциональности .

В теории искусства и художественной практике сложилось устойчивое определение: «Пропорция — закономерное соотношение величин частей художественного произведения между собой, а также каждой части с произведением в целом» .

В философии культуры это понятие рассматривают более широко, как способ установления оптимальной и целостной формальной структуры применением метода количественного согласования частей и целого, но отличают это понятие от категории содержательной целостности — композиции .

В архитектурной теории, напротив, используют более узкое определение: пропорция — это соотношение между длиной, шириной и высотой здания, фасада или его частей. Теоретическое изучение пропорций в архитектуре известно как теория пропорций .

Понятие пропорционирования в истории и теории классического искусства

Достаточно сложная теория пропорций существовала в Древнем Египте , причём не только в математике, но и в искусстве . От египетских жрецов математическую теорию пропорций унаследовали древние греки и римляне. Принято считать, что первым греческое слово «аналогия» ( др.-греч. ἀναλογία ), что дословно означает «вновь-отношение», заменил латинским аналогом лат. proportio римский оратор Цицерон .

Исследования пифагорейцев позволили разделить содержание понятий «соразмерность» и «пропорциональность». Древнеримский архитектор Витрувий в трактате « Десять книг об архитектуре » (13 г. до н. э.) назвал симметрией «простую соразмерность», или метрическую норму, словом «симметрия», а закономерную повторяемость, ритмическую, или динамическую, организацию элементов композиции — пропорцией .

Витрувий добавил к этому понятие модуса ( лат. modus — мера, величина, протяжение, положение). Модальность, или ладовость, — согласованность всех частей формы на основе какого-либо элемента, чаще всего модуля (наименьшей части принимаемой за единицу измерения). Модальность придает пропорциональному строю эмоциональную окраску, определённую тональность (в современной теории гармонии эти понятия распространяют на цветовые и звуковые отношения). Практические способы и приёмы пропорционирования основаны на различении понятий «отношение» и «пропорция». Отношения величин или частей целого друг к другу бывают разного рода. Самые простые — кратные, выражающиеся целыми числами. Например, отношения сторон квадрата (1:1) или прямоугольника, состоящего из двух квадратов (1:2). Однако замечено, что такие отношения негармоничны. Практический опыт показывает, что наиболее приятными для восприятия (зрительного в изобразительном искусстве и слухового в искусстве музыки) являются не кратные, а иррациональные отношения, выражаемые бесконечной дробью. Не случайно подобными отношениями, проверенными временем, характеризуются лист писчей бумаги, формат книги, формы оконных и дверных проёмов, столешниц и филёнок в классической архитектуре и искусстве мебели. Множество отклонений от идеальных отношений, характеризующихся приблизительно 1:1,6, обусловлены внешними факторами и только подтверждают закономерную тенденцию. Подобные отклонения «возмущают душу» и противоречат эстетическому чувству .

Пропорционированием в теории гармонии, как и в математике, именуют равенство двух или более отношений. Соответственно наилучшая пропорция та, в которой уравнены отношения частей и каждой части к целому. Она и называется золотым сечением , или Божественной пропорцией ( лат. Sectio Aurea; Proportia Divina ).

Древнегреческий философ Платон (ок. 427—347 гг. до н. э.) упоминал геометрический способ удвоения площади квадрата построением на его диагонали бóльшего квадрата. Второй квадрат содержит четыре «половинки» первого, следовательно, его площадь вдвое больше . Это простейшее построение содержит в себе важную закономерность. Диагональ квадрата представляет собой иррациональную величину. Если мы примем сторону квадрата за 1, то его диагональ равна или 1,414… Таким образом, система мер, основанная на квадрате и его диагонали, несет в себе двойственность, полифонический принцип отношений простых целых и иррациональных чисел.

В истории античного искусства известен термин «квадратные фигуры» (( др.-греч. τετραγωνος ). Древнеримский писатель Плиний Старший (23—79 гг. н. э.) называл «выглядящими квадратными» ( лат. signa quadrata ) бронзовые статуи аргосской школы, в частности знаменитые « Дорифор » и « Диадумен » работы скульптора Поликлета . При этом он ссылался на энциклопедиста Марка Теренция Варрона (116—27 гг. до н. э.), предполагая, что слово «квадратный» может указывать не характер силуэта статуи, а способ пропорционирования, изложенный в теоретическом сочинении Поликлета « Канон » (сочинение не сохранилось) .

Статуи атлетов в изображении Поликлета действительно выглядят «квадратными» (в ином переводе «широких пропорций»). При анализе их пропорций оказывается, что модулем фигуры является сторона квадрата, диагональ которого, в свою очередь, служит стороной бóльшего квадрата, и т. д. В результате все части статуи выстраиваются пропорционально в системе «парных мер»: рациональных и иррациональных отношений. Так, высота всей фигуры делится кратно на две, четыре и восемь частей (голова фигуры составляет 1/8 роста). Однако при пластическом движении (опоре атлета на одну ногу, вторая нога согнута в колене и отставлена назад) возникают иррациональные отношения. Если мы примем за единицу (сторона малого квадрата) верхнюю часть фигуры (независимо от её действительного размера) — голову и торс до гребня подвздошной кости (на которую ложатся косые мышцы) — за единицу, то нижняя часть фигуры (тазовый пояс и опорная нога) будут равняться 1,618 (сторона бóльшего квадрата). Соответственно вся высота фигуры — 2,618. Эти отношения связаны закономерностью « золотого сечения », открытой ещё древними египтянами и являющейся универсальной .

Часто встречающиеся в популярной литературе отсылки к якобы неизменным, наиболее гармоничным каноническим величинам не имеют достаточного научного обоснования. Обмеры античных статуй, на которые опираются подобные теории, в частности приведённые в классических исследованиях А. Цейзинга : «О пропорциях человеческого тела..» (1854) и «Эстетические исследования» (1854) , имеют случайный, изменчивый характер и сделаны «весьма небрежно»

Выводы об абсолютных и неизменных гармоничных числах, якобы содержащихся в выдающихся произведениях искусства, бесполезны по нескольким причинам. Во-первых, самые выдающиеся античные статуи являются не копиями, а позднейшими и приблизительными репликами несохранившихся оригиналов, весьма различающимися в деталях, поскольку мастера римской и неоаттической школ не видели оригиналов и опирались лишь на приблизительные литературные описания и другие реплики в иных материалах и размерах. Во-вторых, все скульптуры даны в разнообразных движениях: наклонах головы, разворотах торса, положений рук и ног. В таких случаях неясно какие точки измерений считать верными: анатомические или зрительные, воспринимаемые в действительных ракурсах. В-третьих, пропорциональные каноны , даже если фиксировались, значительно менялись на протяжении веков и даже десятилетий, они зависели от эпохи, особенностей манеры, времени и места работы мастеров и школ . Например, в скульптурах периодов классики, века Поликлета и Фидия, и эллинизма , в произведениях Лисиппа и Праксителя. То же относится и к архитектуре. Очевидно, что секрет гармонии пропорций заключён не в «идеальных числах», а в закономерностях подвижных, динамичных пропорциональных отношений .

Характерно также, что теорию пропорционирования усиленно разрабатывали в периоды наиболее рационального отношения к природе и искусству. Так с 1496 года в Милане подобную теорию попытались создать совместно художник Леонардо да Винчи и математик Лука Пачоли в трактате « Божественная пропорция » ( лат. De Divina Proportione ). Основной текст и математические выкладки, а также издание книги, осуществил Л. Пачоли. Сохранилось две рукописи этого трактата — одна в Публичной библиотеке в Женеве, вторая — в Амброзианской библиотеке в Милане. Леонардо выполнил иллюстрации, в том числе, возможно, рисунок, известный под названием « Витрувианский человек ». Трактат был завершён 14 декабря 1498 года. По рисункам Леонардо были сделаны гравюры на дереве. Трактат издан в Венеции в 1509 году .

Теорию пропорций разрабатывали многие художники эпохи Возрождения: Лоренцо Гиберти , Леон Баттиста Альберти , Альбрехт Дюрер , позднее И. Д. Прейслер .

Способы пропорционирования в истории архитектуры

В практике строительства зодчие разных времен до возникновения научной теории гармонии, как правило, интуитивно следовали закономерностям гармонизации формы. Эти навыки передавали от отца к сыну многими поколениями мастеров странствующих строительных артелей («вольных каменщиков» — масонов ). В отличие от иррациональных глубин творчества числовые закономерности отношений величин подлежат точному расчету, анализу, фиксированию, и, следовательно, их легче передавать от одного поколения мастеров к другому, от учителей к подмастерьям в качестве «секретов мастерства».

Интуитивным критерием гармонии пропорций служила «золотая середина» ( лат. aurea mediocritas ), а образцом — отношения величин, наблюдаемые в природе. Так древние эллины в своей архитектуре использовали целые числа, кратные модули и рациональные приёмы, но вводили «оптические поправки» и нюансирование, придававшие отношениям величин легкую неправильность. Таковы курватура ( лат. curvatura — кривизна, искривление прямых линий и плоскостей), энтазис ( др.-греч. ἔντασις — напряжение) — лёгкое утолщение колонн в средней части, контракция (нарушение равенства интерколумниев , сближение расстояний между колоннами).

Они также использовали эпиморные отношения ( др.-греч. επι — сверх, над и др.-греч. μοριον — часть, частица), в которых, в отличие от простых кратных (1:2; 1:3; 1:4), превышение большей части равняется одной доле меньшей (например: 2:3; 3:4; 8:9), что практически близко отношениям «золотых отрезков». Такой способ проявился, в частности, при расчете количества колонн древнегреческих храмов на переднем и боковых фасадах по эпиморной формуле: n : (n + 1), когда на боковом фасаде количество колонн на одну больше, чем на переднем. Именно такую закономерность греки называли «аналогией».

В Национальном археологическом музее в Неаполе и в музее Терм в Риме , хранятся необычные предметы, найденные при раскопках Помпей и условно называемые пропорциональными циркулями . Они различаются в деталях, но сходятся в главном — две деревянные планки крестообразно скреплены неподвижным шарниром. Отношения их сторон соответствуют правилу «золотого сечения». Археологи находят схожие инструменты в разных регионах античного мира. Вероятно, они служили эталонами пропорциональных модулей в архитектуре .

Система пропорционирования в архитектуре всегда была тесно связана с техникой и технологией строительства, развитием геометрии и способами измерения величин. Необходимость разбивки плана здания на земле в натуральную величину способствовала развитию приёмов построения определённых пропорциональных отношений как в горизонтальной, так и в вертикальной плоскостях. Простейший способ такого пропорционирования сводился к построению прямого угла на земле, от которого зависело проецирование центра тяжести будущего сооружения на середину основания (перпендикуляра от вершины к плоскости земли) — первого условия прочности и надёжности постройки. Древние зодчие решали эту задачу гениально просто. Они брали мерный шнур — верёвку, разделённую узлами на двенадцать равных частей, соединяли её концы (двенадцатый и нулевой узел) и, растягивая на земле, забивали колышки в землю на третьем, седьмом и двенадцатом делениях. При этом получался треугольник с отношениями сторон 3 : 4 : 5. Такой треугольник, согласно одной из аксиом геометрии и теоремы Пифагора, всегда будет прямоугольным. Получив прямой угол без всяких вычислений, строители могли его увеличивать до нужных размеров, переносить в вертикальную плоскость. Благодаря своим универсальным свойствам такой треугольник в истории архитектуры получил название: « египетский священный треугольник » . Одна из гигантских пирамид в Гизе — пирамида Хефрена — представляет собой в поперечном сечении два «священных треугольника», а отношение высоты к стороне квадратного основания составляет 2:3 (143,5 : 215,25 м). За долгое время эти размеры несколько уменьшились (136,4 : 210,5 м).

Числа треугольника: 3, 4, 5, их сумма 12, а также 7, сумма 3 и 4, — постоянно встречаются в природе и также почитались священными. Согласно религиозным представлениям, универсальная геометрия египетского треугольника олицетворяла Великую триаду богов: Исида и Осирис (два катета) и их сын Гор (гипотенуза). «Бытие и небытие сопоставляются с Исидой и Осирисом, а диагональ с Гором-Соколом» ( егип. ḥr — «высота», «небо») .

Древние греки называли строителей египетских пирамид «гарпедонавтами» («натягивателями верёвок» от др.-греч. αρπεδονη — аркан, петля). Французский архитектор А. Фурнье де Кора, норвежская художница Е. Килланд и русский архитектор В. Н. Владимиров , изучая приемы пропорционирования древних зодчих, независимо друг от друга пришли к модели, объединяющей геометрические фигуры и численные отношения, закономерно повторяющиеся в планах и разрезах древних сооружений. Такая модель получила название «египетской системы диагоналей» .

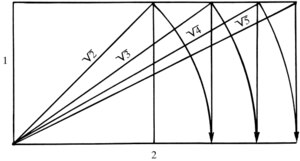
Если мы возьмём квадрат (с отношением сторон 1:1) и спроецируем его диагональ (равную квадратному корню из двух) на продолжение одной из сторон, а затем из найденной точки восстановим перпендикуляр, то получим новую фигуру — прямоугольник. Проведя и в нём диагональ, обнаружим, что она равна квадратному корню из трёх. Повторим построение и увидим новый прямоугольник с более длинной стороной. Диагональ этого прямоугольника будет равняться квадратному корню из четырёх, то есть 2. Проецируя эту диагональ как в предыдущих случаях и восстановив перпендикуляр, получаем так называемый двусмежный квадрат (состоящий из двух равных квадратов) с диагональю равной квадратному корню из пяти. Внутри двусмежного квадрата (два квадрата чаще всего образуют планы древнеегипетских храмов) помещается ряд диагоналей, и соответственно иррациональных величин, связанных определённой последовательностью.

Отношение стороны квадрата к его диагонали часто использовалось в пропорциональных построениях, так как позволяло легко образовывать непрерывный ряд взаимосвязанных величин. Система вписанных или описанных квадратов с диагоналями была удобна, ибо давала архитектору своеобразную пропорциональную шкалу, на основании которой он мог строить соразмерность частей здания.

Геометрический способ построения «золотого сечения» идеально прост, поскольку не требует никаких вычислений и предполагает всего два движения циркулем. Он не изменился до настоящего времени и называется «способом архитекторов» . Малый катет «египетского треугольника» (размером 1) откладывается с помощью циркуля или мерного шнура на пифагоровой гипотенузе (она же диагональ двусмежного квадрата, равная квадратному корню из пяти). Затем остаток диагонали (квадратный корень из пяти минус единица) переносится противоположным движением циркуля на большой катет (равный двум). В результате большой катет будет разделён на две неравные части, при одном взгляде на которые ощущаются гармонические отношения. Эти ощущения можно проверить вычислением. Обозначим бóльшую часть разделённого на части катета литерой «А», а меньшую — «В». Тогда отношение всего катета (А+В) к его бóльшей части (остатку диагонали) будет составлять два, делённое на квадратный корень из пяти минус единица. При любых значениях это отношение будет выражаться иррациональным числом, бесконечной дробью: 1,618033… Если же проверить отношение бóльшей части (А) к меньшей части заданного отрезка (В), то мы, на удивление, получим то же самое число: 1,618033… Такую формулу можно записать следующим образом: (А+В) : А = А : В (целое относится к бóльшей части так же, как бóльшая часть относится к меньшей). От перемены мест членов этой пропорции результат не меняется.

Эстетический смысл формулы заключается в том, что данная пропорция является наилучшей и единственно возможной — тем идеальным случаем, когда уравниваются отношения частей какой-либо величины (формы) между собой и каждой из этих частей к целому. Все прочие гармонические отношения связывают только отдельные части формы, а «золотая пропорция» связывает все части и целое. Иначе говоря, в «формуле красоты» единой закономерностью связаны отношения частей и целого. По замечанию Платона, «наилучшая аналогия делает целое и его части нераздельными». Причём все величины можно дробить до бесконечности и они будут сохранять свои «золотые свойства». Прочие способы и приёмы гармонизации имеют частный характер, а «золотая пропорция» — всеобщий. Отсюда и название.

Наиболее яркий пример действия этой закономерности — отношения плана и фасада Парфенона в Афинах (447—438 гг. до н. э.) — общепризнанного эталона гармонии. Исследователей всегда удивляло в обмерах этого шедевра архитектуры наличие некратных мер и иррациональных отношений, в частности, отклонение плана храма от традиционного размера в два квадрата. Правило «золотой пропорции» объясняет эту «странность». Если спроецировать диагональ двусмежного квадрата стилобата Парфенона на продолжение его длинной стороны, то мы получим действительные отношения плана этой постройки: единица к квадратному корню из пяти. Иначе говоря, если ширину главного фасада храма (30,89 м) принять за 1, то отношение ширины к длине бокового фасада по стилобату (69,54 м) будет составлять единица к квадратному корню из пяти. Такими же отношениями связаны все размеры внутреннего пространства: наоса , пронаоса и опистодома .

Главный фасад Парфенона (без треугольного фронтона) вписывается в двусмежный квадрат. Колонна вместе с капителью (10,43 м) составляет меньший член «золотой пропорции». Бóльший отрезок «золотого сечения» соответствует общей высоте здания вместе с кровлей. Те же отношения повторяются в деталях вплоть до мельчайших . Исходное «золотое число» (1,618033…) принято обозначать для краткости греческой буквой φ («фи»), с которой начинается имя выдающегося скульптора и архитектора античности Фидия, одного из создателей Парфенона.

Аналогичные приёмы использовали древнерусские зодчие. Плотницких дел мастера осуществляли разметку плана сооружения прямо на земле без вычислений на основе квадрата и его диагонали. Для этого они использовали мерный шнур и деревянные колышки, вбитые в землю. Основной мерой была длина бревна, а модулем клеть из уложенных друг на друга венцов — связанных по углам четырёх брёвен, образующих квадрат. Задачу построения прямого угла решали с помощью двух мерных шнуров — способом уравнивания диагоналей окладного (нижнего) венца (равенство диагоналей даёт квадрат). Следующая задача: проецирование диагонали (или её производной) на продолжение стороны квадрата давало второй модуль, равняющийся стороне квадрата удвоенной площади. На земле расчерчивали план будущего сооружения, к примеру, церкви — основной клети (так называемая клетская церковь) с пристроенными к ней притвором и алтарём. Закономерно, что древнерусские плотники самостоятельно нашли простейшее практическое решение задачи, хорошо известной в античности .

Историк и археолог Б. А. Рыбаков в 1950-х годах изучал древнерусские «вавилоны» — графические знаки, состоящие из подобных прямоугольников или квадратов, вписанных один в другой. Они встречаются в раскопках на глиняных черепках (керамидах) и каменных плитах, с XVII века — в русских летописях. По мнению исследователя, «вавилоны» представляют собой схематическое изображение Вавилонской башни и одновременно символ пропорционального канона .

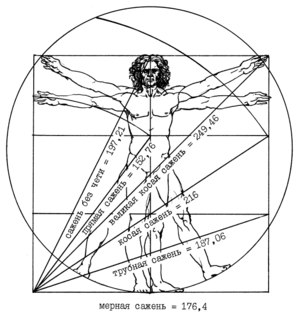
Со временем на основе простого плотницкого опыта в Древней Руси сложилась изысканная система пропорционирования на основе «системы парных мер»: рациональных и иррациональных чисел. Об этом свидетельствуют обмеры храмов. Изучение древнерусских мер длины по данным Б. А. Рыбакова и других исследователей подтверждает этот факт. Строители в качестве мер длины использовали не одну, и не две сáжени , а шесть основных и одну дополнительную. Мерный шнур древнерусских плотников называли «сокарь» (от др.-греч. σωχος — сильный), Размеры саженей менялись, однако закономерность пропорционирования заключалась не в некой идеальной мере, а в их отношениях и, прежде всего, к размерам фигуры человека. Эта античная традиция, именуемая антропоморфизмом , сохранялась в византийском и древнерусском искусстве.

Сравнив отношения нескольких саженей, использовавшихся в древнерусском строительстве, и построив «вавилон» (по Б. А. Рыбакову), можно, допустив известную вольность, вписать в этот «вавилон» фигуру человека по известному рисунку Леонардо да Винчи , связанному, как предполагают, с трактатом об архитектуре Витрувия (« Витрувианский человек »; лат. Homo vitruvianus ). Антропоморфность древнерусских мер длины очевидна, как и аналогия мерных систем средневековой Руси и европейского Запада.

Западноевропейские средневековые строительные артели использовали в основном два способа геометрических построений. Самый простой способ расчёта размеров, восходящий к античным «квадратным фигурам», так и называли: квадратурой . Этот способ впервые описан германским масоном (вольным каменщиком) из Регенсбурга , строителем соборов Маттеусом Рорицером в 1486 году. Он получил название «германского». Всю постройку вписывали в квадрат (в плане и высотных отношениях), а производные величины определяли диагональю квадрата, построенного на ширине главного фасада здания. Такой пример на основе обмеров фасада собора Нотр-Дам в Париже приводит в своей знаменитой книге Огюст Шуази .

Другой способ получил наименование триангуляция . Этому способу также придавали мистическое значение, в особенности при строительстве храмов, поскольку равносторонний треугольник — символ Пресвятой Троицы . Практически, согласно реконструкции Б. Р. Виппера , это выглядело следующим образом. На выбранной строительной площадке ровно в полдень в землю вкапывали жердь — гномон (указатель), обозначающий центр главного, западного фасада будущего здания. Полуденное солнце в средних широтах отбрасывает тень от гномона точно на север, и в этом направлении откладывали половину ширины фасада. Другую половину отмеряли в противоположную сторону. Затем на полученной ширине главного фасада с помощью мерных шнуров выстраивали на земле равнобедренный (в иных случаях равносторонний) треугольник. Его вершина отмечала половину длины главного нефа будущего храма. Потом зеркально выстраивали второй треугольник. Медиана треугольников, перпендикулярная к линии фасада определяла среднюю линию главного нефа храма, ориентированную по оси запад—восток. Основания треугольников делили на четыре равные части. Это давало правильное соотношение ширины главного нефа и двух боковых, которые полагалось делать вдвое уже. Точки пересечения малых треугольников намечали места будущих опор. Такую триангуляцию можно было дробить до бесконечно малых величин, переносить в вертикальную плоскость, определяя основные конструктивные точки фасадов и внутреннего устройства здания .

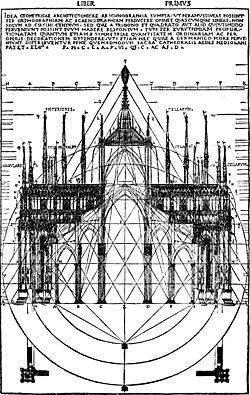
При закладке Миланского собора в 1387 году пригласили зодчих из Германии и Франции, которые поспорили: строить ли храм по «германскому способу» (ad quadratum) — на основе квадрата и его диагонали — или по «французскому способу» (ad triangulum) — на основе равностороннего треугольника. Чертёж поперечного сечения Миланского собора (по средокрестию), выполненный в 1391 году Габриэле Сторналокко из Пьяченцы, приведён в итальянском издании трактата Витрувия «Десять книг об архитектуре» Чезаре Чезариано 1521 года. Этот чертёж наглядно демонстрирует «связанную систему», в которой основные конструктивные точки собора вписаны не только в равносторонние треугольники, но и в концентрические окружности. Такая «связанная система» придаёт наибольшую прочность и зрительную цельность всему сооружению.

Теорию пропорционирования в архитектуре в эпоху Возрождения разрабатывали Леон Баттиста Альберти , Андреа Палладио , Н. А. Львов . В Новое Время — И. В. Жолтовский , О. И. Гурьев , И. П. Шмелёв.

Известно, что Андреа Палладио не пользовался сложными вычислениями и иррациональными числами. В своём трактате « Четыре книги об архитектуре » (1570) он не упоминает о правиле золотого сечения, но предлагает пропорционировать здания «в один или два куба». Однако в постройках Палладио повторяются отношения: 2: 3: 5. Венецианский архитектор также прибегал к построениям подобия разновеликих прямоугольников на основе параллельных или перпендикулярных диагоналей (одна из аксиом геометрии). Такой приём получил в истории архитектуры название «правило прямого угла». Одним из символов гармонии пропорций в истории архитектуры является знаменитая постройка Палладио Вилла Ротонда .

Исследователь творчества Палладио, архитектор О. И. Гурьев подчёркивал, что, не упоминая о «золотом сечении», но следуя «правилу подобных прямоугольников и кубов», и выстраивая их на параллельных либо перпендикулярных диагоналях, Палладио устанавливал отношения величин, которые определяются «членами ряда Фибоначчи или родственны им: 9:5 есть утроенное отношение 3:5, а 3:1 — удвоенное отношение 3:2, и т. д.» .

Соотношение гармонических интервалов в музыке и архитектуре в XVIII веке в Риме изучал французский архитектор и теоретик Антуан Деризе . В ХХ веке российский архитектор и педагог П. А. Кудин продолжил эту традицию, подробнейшим образом на основе математических расчётов «пифагорейского звукоряда» вывел такие соотношения, «привязав» их к шкале спектральных цветов и соразмерности тела человека .

В XX столетии знаменитый французский архитектор-модернист Ле Корбюзье создал на основе традиционной системы парных мер, «правила прямого угла» и двух «шкал» (рациональных и иррациональных величин) свой знаменитый « Модулор » .

Петербургский архитектор и теоретик искусства Игорь Павлович Шмелёв, изучая закономерности гармонии, создал собственную интерпретацию канона древнеегипетских жрецов на основе анализа деревянных досок из гробницы Хеси-Ра, жреца бога Гора и главного архитектора фараона Джосера в Саккара .

В истории изобразительного искусства теме пропорционирования посвятил одну из своих теоретических работ 1783 года живописец, сэр Джошуа Рейнольдс , а также английский гравёр Джон Томас Смит , назвавший свою теорию «правилом третéй». Идеальный пример «золотого сечения» мы находим в композиции картины голландского художника Яна Вермеера Делфтского « Маленькая улица ».

См. также

• Божественная пропорция
• S-образная линия
• Figura serpentinata
• Золотой прямоугольник
• Канон (искусство)
• Модулор

Примечания

Литература

• Волошинов А. В. Математика и искусство. — М.: Просвещение, 1992. — 336 с., ил.
• Гурьев О. И. Композиции Андреа Палладио : Вопросы пропорциональности. — Л. : Изд-во ЛГУ, 1984.
• Шевелев И. Ш., Марутаев М. А., Шмелев И. П. Золотое сечение: Три взгляда на природу гармонии. — М.: Стройиздат, 1990. — 343 с., ил.
• Шмелев И. П. Архитектор фараона. — СПб.: Искусство России, 1993. — 95 с., ил.