Группа бордюра — это математическое понятие, используемое для классификации согласно симметриям узоров на двумерных поверхностях, повторяющихся в одном направлении. Такие узоры встречаются часто в архитектуре и декоративном искусстве . Математическое изучение таких узоров показывает, что существует в точности семь типов симметрии.

Группы бордюра являются двумерными , имеющими повторение лишь в одном направлении. Они связаны с более сложными группами орнамента , которые классифицируют узоры, повторяющиеся в двух направлениях, и кристаллографическими группами , которые классифицируют узоры, повторяющиеся в трёх направлениях.

Общее описание

Формально, группа бордюра — это класс бесконечных дискретных групп симметрии узоров на ленте (бесконечно широком прямоугольнике), а следовательно, это класс групп движений на плоскости или ленте. Группа симметрии группы бордюра необходимым образом содержит параллельные переносы и могут содержать скользящие симметрии , отражения вдоль оси ленты, отражения поперёк оси ленты и вращения на ${\displaystyle 180^{\circ }}$ . Существует семь групп бордюра, они показаны ниже в таблице. Многие авторы перечисляют группы бордюра в другом порядке .

Фактические группы симметрии внутри группы бордюра характеризуются наименьшим расстоянием параллельного переноса и, для групп бордюра с вертикальной симметрией или поворотом на ${\displaystyle 180^{\circ }}$ (группы 2, 5, 6 и 7), местоположением оси симметрии или центра поворота. В случае групп симметрии на плоскости дополнительными параметрами являются направление вектора переноса и, для групп бордюра с горизонтальной осью симметрии, скользящая симметрия, или поворот на ${\displaystyle 180^{\circ }}$ (группы 3-7), положение оси отражения или центра вращения. Таким образом, имеется две степени свободы для группы 1, три для групп 2, 3, 4 и четыре для групп 5, 6 и 7.

Для двух из семи групп бордюра (группы 1 и 4) группы симметрии порождаются одним элементом , для четырёх групп (группы 2, 3, 5 и 6) они порождаются двумя генераторами, а для группы 7 группы симметрии требуют три генератора. Группа симметрии в группах бордюров 1, 2, 3 или 5 является подгруппой группы симметрии последней группы бордюра с тем же расстоянием параллельного переноса. Группа симметрии в группах бордюра 4 и 6 является подгруппой группы симметрии последней группы бордюра с половинным расстоянием параллельного переноса. Последняя группа обоев содержит группу симметрии простейшего периодического узора на полосе (или плоскости) — последовательности точек. Любое преобразование плоскости, оставляющее нетронутым этот узор, может быть разложено на параллельный перенос ( x , y ) → ( n + x , y ) и, возможно, отражение относительно горизонтальной оси ( x , y ) → ( x ,− y ) или вертикальной оси ( x , y ) → (− x , y ) в предположении, что оси выбраны посередине двух соседних точек, или вращение на угол ${\displaystyle 180^{\circ }}$ , ( x , y ) → (− x ,− y ). Таким образом, группа бордюра содержит «наибольшую» группу симметрии, которая состоит из всех этих преобразований.

Требование дискретности вводится для исключения групп, содержащих все преобразования и групп, содержащих произвольно малые параллельные переносы (например, группы горизонтального переноса на любое рациональное расстояние).

Требование бесконечности вводится для исключения групп, не имеющих параллельного переноса:

• группа только с из тождественным движением (изоморфна C ₁ , тривиальная группа порядка 1).
• группа, состоящая из тождественного движения и отражения относительно горизонтальной оси (изоморфна C ₂ , циклическая группа порядка 2).
• группы, состоящие из тождественного движения и отражения относительно вертикальной оси
• группы, состоящие из тождественного движения и поворота на ${\displaystyle 180^{\circ }}$ вокруг точки, находящейся на горизонтальной оси
• группы, состоящие из тождественного движения и отражения относительно вертикальной оси, отражения относительно горизонтальной оси и поворота на ${\displaystyle 180^{\circ }}$ вокруг точки пересечения этих осей (изоморфна четверной группе Клейна )

Описание семи групп бордюра

Существует семь различных подгрупп (с точностью до масштаба) в группе дискретных бордюров, генерируемых параллельным переносом, отражением (вдоль оси бордюра) и поворотом на ${\displaystyle 180^{\circ }}$ . Каждая из этих подгрупп является группой симметрии бордюра и простые бордюры показаны на рис. 1. Семь различных групп соответствуют семи бесконечным сериям групп осевой симметрии трёхмерного пространства , с ${\displaystyle n=\infty }$ .

Группы бордюра обозначаются с использованием нотации Германа — Могена , международной кристаллографической нотации , , и с помощью символов Шёнфлиса :

IUC		Шён- флис * Группа	Диаграмма §	Примеры обозначение Конвея	Описание
p1	[∞] +	C ∞ Z ∞	∞∞	F F F F F F F F hop (скакать на одной ноге)	(T) Только параллельный перенос: Эту группу создаёт один генератор, перенося на наименьшее расстояние для данного периодического узора.
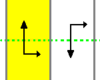
p11g	[∞ + ,2 + ]	S ∞ Z ∞	∞×	FℲ FℲ FℲ FℲ FℲ step (шаг)	(TG) Скользящая симметрия и перенос: Эта группа создаётся одним генератором (скользящей симметрией), параллельный перенос получается как результат двух скользящих симметрий.
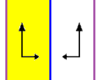
p1m1	[∞]	C ∞v	*∞∞	Λ Λ Λ Λ Λ Λ Λ Λ sidle (идти боком)	(TV) Отражение относительно вертикальной оси и перенос: Группа та же самая, что и нетривиальная группа одномерного случая. Группа строится с помощью параллельного переноса и отражения относительно вертикальной оси.
p2	[∞,2] +	D ∞ Dih ∞	22∞	S S S S S S S S spinning hop (скачки с поворотом)	(TR) Перенос и поворот на ${\displaystyle 180^{\circ }}$ : Группа создаётся двумя генераторами — переносом и вращением на ${\displaystyle 180^{\circ }}$ .
p2mg	[∞,2 + ]	D ∞d Dih ∞	2*∞	V Λ V Λ V Λ V Λ spinning sidle (боковые скачки с поворотом)	(TRVG) Отражение относительно вертикальной оси, скользящая симметрия, перенос и поворот на ${\displaystyle 180^{\circ }}$ : Параллельный перенос здесь получается как результат двух скользящих симметрий, так что группа генерируется скользящей симметрией и либо вращением, либо вертикальной симметрией.
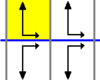
p11m	[∞ + ,2]	C ∞h Z ∞ ×Dih 1	∞*	B B B B B B B B jump (прыжок)	(THG) Перенос, отражение относительно горизонтальной оси, скользящая симметрия: Эта группа генерируется переносом и отражением относительно горизонтальной оси. Скользящая симметрия получается как перенос + отражение.
p2mm	[∞,2]	D ∞h Dih ∞ ×Dih 1	*22∞	H H H H H H H H spinning jump (прыжок с поворотом)	(TRHVG) Отражения относительно вертикальной и горизонтальной осей, параллельный перенос и вращение на ${\displaystyle 180^{\circ }}$ : Для этой группы нужны три генератора. Один из генерирующих наборов состоит из переноса и отражений относительно обоих осей.

^* Нотация Шёнфлиса для точечной группы здесь расширена для случая бесконечного набора эквивалентных диэдральных точечных симметрий

^§ Диаграмма показывает одну фундаментальную область , выделенную жёлтым цветом. Оси отражения показаны синим цветом, оси скользящей симметрии показаны зелёным пунктиром, а точки вращения показаны зелёными квадратиками.

Как мы видим, с точностью до изоморфизма , существует четыре группы, две абелевы , и две неабелевы.

Типы решёток: наклонная и прямоугольная

Группы можно классифицировать по типу их двумерной решётки . Наклонная решётка означает, что второе направление не обязательно ортогонально направлению повторения.

Веб-демонстрации и программное обеспечение

Существуют программные графические инструменты, создающие двумерные узоры с помощью групп бордюра. Обычно весь узор обновляется автоматически при редактировании фрагмента.

• от 29 ноября 2017 на Wayback Machine , Свободное приложение для обоев, бордюров и других узоров.
• от 21 ноября 2020 на Wayback Machine , свободно загружаемая программа Kali для Windows и Mac Classic.
• от 28 декабря 2017 на Wayback Machine , Программа ( nagware ) замощения для различных платформ, поддерживающая обои, бордюры, а также мозаик Хееша .
• от 22 января 2007 на Wayback Machine , свободно распространяемый стек (приложение для Hypercard) для HyperCard для платформы Classic Mac, поддерживающий группы бордюра.

Примечания

Литература

Ссылки

• от 20 июня 2017 на Wayback Machine на cut-the-knot
• от 21 октября 2017 на Wayback Machine