Interested Article - Четырёхугольник Ламберта

- 2021-03-04
- 1

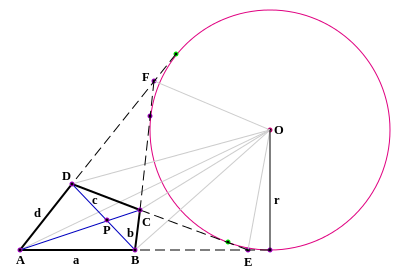
Четырёхугольник Ла́мберта , или трипрямоуго́льник , — четырёхугольник , имеющий при трёх его вершинах прямые углы .
Назван в честь швейцарского математика Иоганна Генриха Ламберта , впервые исследовавшего свойства такой фигуры в попытках доказательства 5-й аксиомы геометрии Евклида .
Свойства
Пусть — четырёхугольник Ламберта на абсолютной плоскости с прямыми углами при , и . Тогда
- и ;
- .
Более того, если одно из этих неравенств превращается в равенство, то на этой абсолютной плоскости верен постулат Евклида о параллельных.
История
Четырёхугольник Ламберта впервые рассмотрен Ибн ал-Хайсамом в XI веке .
Рассматривался Иоганном Ламбертом в 1766 при попытках доказать постулат Евклида о параллельных . Из трёх возможных предположений о величине четвёртого угла: либо угол прямой, либо угол тупой, либо угол острый; первая гипотеза является утверждением, эквивалентным постулату Евклида о параллельных; вторая приводит к противоречию с другими аксиомами и постулатами Евклида. Относительно третьей гипотезы Ламберт сделал предположение, что она выполняется на некоторой мнимой сфере. После чего сделал ошибочное утверждение, что такой сферы в реальном пространстве быть не может и поэтому постулат верен.
В 1733 году Джироламо Саккери рассматривал четырёхугольники с двумя прямыми углами — так называемые четырёхугольники Саккери .
Примечания
- . Дата обращения: 25 мая 2012. 13 декабря 2019 года.
Литература
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М. : Просвещение , 1991. — С. 365—366. — 383 с. — ISBN 5-09-001287-3 .
- 2021-03-04
- 1